2.2 Ortsabhängige Kräfte

Wir wollen den Begriff Arbeit (Energie) auf ortsabhängige Kräfte erweitern und definieren

als die Arbeit, die aufgewandt werden muss, um einen Massenpunkt von 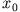nach 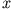zu bewegen. Dann gilt wie im vorigen Abschnitt

Die Arbeit 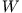, die aufgebracht wird, erzeugt eine Änderung in der kinetischen Energie.

Bemerkungen:

(i)

Die Arbeit hängt offenbar nur von Anfangs- und Endpunkt der Bewegung ab. Man kann also eine Potentialfunktion 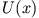definieren mit den Eigenschaften

(ii)

Aus der Definition der Energie erhält man durch Umordnung

den Energieerhaltungssatz:
In einem rein ortsabhängigen Kraftfeld ist die Energie eine Erhaltungsgröße. Kräfte, für die die Energie konstant ist nennt man konservativ. Kennzeichnend für konservative Kräfte ist, dass man sie aus einer Potentialfunktion ableiten kann

Beispiele

B2.5 Ein Körper fällt aus unendlicher Entfernung radial auf die Erde zu

Mit welcher Geschwindigkeit trifft er die Erdoberfläche ?

Abbildung 2.6: Freier Fall aus unendlicher Entfernung

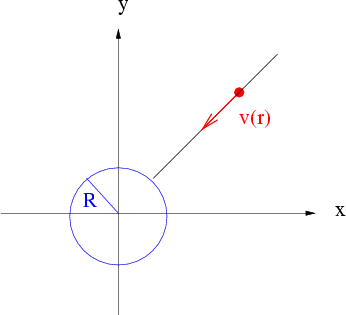Wir wollen annehmen, der Massenpunkt befinde sich anfänglich in Ruhe 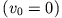. Aus dem Energieerhaltungssatz erhalten wir dann

B2.6 Wie groß muss die Geschwindigkeit eines Massenpunktes sein, um das Gravitationsfeld der Erde zu verlassen ?

Dabei handelt es sich um die Umkehrung der Aufgabenstellung B 2.5.
Die Fluchtgeschwindigkeit von der Erdoberfläche beträgt

Ein interplanetares Raumschiff (z.B. Flug Erde-Mars) muss diese Geschwindigkeit erreichen.