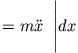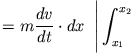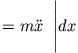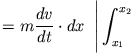2.1.2 Arbeit und Energie bei konstanter Kraft

Ausgangspunkt ist die Bewegungsgleichung, die wir über die Ortskoordinate integrieren werden

Für die rechte Seite (rhs) erhält man

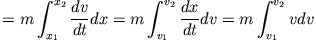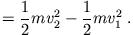Dabei ist 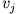die Geschwindigkeit des Massenpunktes am Ort . Die linke Seite (lhs) ergibt, da 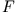konstant ist,

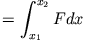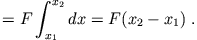Somit erhalten wir folgende Aussage

Bemerkungen

(i)

Die Einheit der Arbeit (Energie) in SI ist

(ii)

Die Umordnung der Terme in (2.3) ergibt

Man definiert 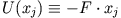als die potentielle Energie eines Massenpunktes am Ort . Damit gilt

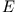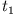
Die mechanische Gesamtenergie eines Masenpunktes bestehend aus seiner potentiellen Energie und seiner kinetischen Energie ist zu den Zeiten 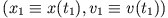und 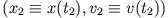identisch. D.h. die Energie 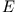ist eine Erhaltungsgröße bei konstanter Kraft.

(iii)

Im Falle der erdnahen Gravitation 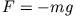ist die potentielle Energie nur davon abhängig, wie hoch man den Massenpunkt über Bodenniveau bringt, da die Gravitationskraft radial zum Mittelpunkt der Erde gerichtet ist. Sei also 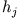die Höhe des Massenpunktes zur Zeit 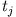bezogen auf die Erdoberfläche, so besitzt der Massenpunkt die potentielle Energie 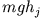und es gilt für die Energieerhaltung

B2.4 Senkrechter Wurf nach oben

Abbildung 2.5: Senkrechter Wurf

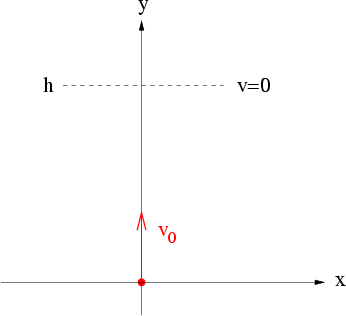Ein Massenpunkt wird mit der Anfangsgeschwindigkeit 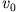senkrecht nach oben geworfen. Man berechne seine maximale Höhe.
Aus der Energieerhaltung folgt, dass die mechanische Gesamtenergie des Massenpunktes am Boden zur Zeit 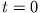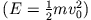identisch sein muss mit der Gesamtenergie, die er im höchsten Punkt (Umkehrpunkt) seiner Bewegung erreicht (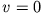, deshalb 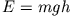). D. h.

Wir konnten diese Lösung so einfach erhalten, weil der Energiesatz bereits ein Integral der Bewegungsgleichung ist, also eine Teillösung der Differentialgleichung. Beachten Sie, wieviel aufwändiger die Berechnung der maximalen Höhe über das Weg-Zeit-Gesetz durchzuführen wäre!