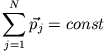1.3.3 Newtons Gesetze (moderne Formulierung)

Nachdem wir kinematische Größen für die Bewegung eines Massenpunktes definiert und über ein geeignetes Maßsystem skaliert haben, können wir jetzt Newtons Gesetze formulieren

(1)

Ein Körper ist in Ruhe oder bewegt sich mit konstanter Geschwindigkeit, wenn keine Kraft auf ihn wirkt

(2)

Die zeitliche Änderung des Impulses (der Impuls ist 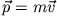) eines Körpers ist gleich der auf den Körper wirkenden Kraft

(3)

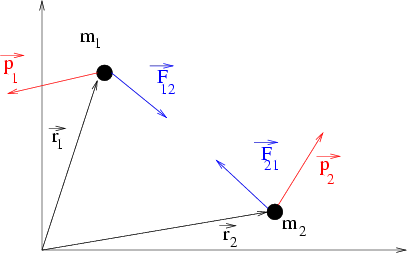
Zwei Körper üben aufeinander betragsmäßig gleiche aber entgegengesetzt gerichtete Kräfte aus (actio gleich reactio). Bezeichnet man mit 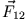die Kraft von Masse 2 auf Masse 1 und mit 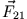die entsprechend umgekehrte Situation, so gilt

Abbildung 1.5: actio = reactio

Diese drei Gesetze sind ausreichend zum Verständnis der klassischen Mechanik: sie beschreiben Bewegungabläufe auf der Erde, im Sonnensystem oder die Dynamik von Galaxien. Allerdings werden wir später einschränkende Bedingungen formulieren. Vereinfacht ausgedrückt lauten die Einschränkungen: Newtons Gesetze gelten für Systeme, die sich deutlich langsamer bewegen als das Licht im Vakuum und makroskopisch sind.

Bemerkungen:

(i)

Newtons Synthese besteht in der Abstraktion, dass die Gesetzmäßigkeiten für die Bewegung von Körpern auf der Erde dieselben sind wie im Weltraum.

(ii)

Das erste Gesetz besagt, dass eine Bewegung mit konstanter Geschwindigkeit der natürliche Zustand eines kräftefreien Körpers ist. Da wir prinzipiell kein absolutes Bezugssystem festlegen können, erlaubt uns das erste Gesetz, jedes beliebige System, das sich mit konstanter Geschwindigkeit bewegt -Inertialsystem- zu wählen: jedes Inertialsystem ist gleichwertig zur Beschreibung physikalischer Vorgänge (Relativitätsprinzip).

(iii)

Aus dem zweiten Gesetz folgt für zeitlich konstante Massen

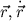Da in der Regel von und 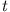abhängt, haben wir eine Bewegungsgleichung für ein klassisches System

Dabei handelt es sich um eine gewöhnliche Differentialgleichung 2. Ordnung zur Bestimmung von Ort 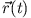und Impuls 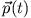eines Systems. Wir müssen die wirkenden Kräfte und den Anfangszustand des Systems kennen 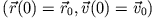, alles andere wird durch die Bewegungsgleichung eindeutig festgelegt.

(iv)

Eine Konsequenz des dritten Gesetzes ist die Impulserhaltung eines abgeschlossenen Systems von Massenpunkten. Darunter versteht man ein System, auf das keine äußeren Kräfte wirken. Für zwei Massenpunkte gilt für deren Summenimpuls

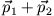
Die entsprechende Erweiterung für N Massenpunkte ist analog

Der Gesamtimpuls eines Systems von Massenpunkten ist zu allen Zeiten gleich und somit eine Erhaltungsgröße, wenn nur innere Kräfte zwischen den Massenpunkten und keine äußeren Kräfte auf das System einwirken.

(v)

.Was ist also eine Kraft ? Darauf gibt uns die Mechanik keine Antwort.
Wie erfahren wir eine Kraft ? Z.B. in Form von Newtons Gravitationsgesetz (Details später)

Es gilt für den fallenden Apfel (M: Masse der Erde, m: Masse des Apfels) wie auch für die Bewegung der Planeten (M: Masse der Sonne, m: z.B. Masse der Erde).
Was bewirkt die Kraft ? Nach dem zweiten Gesetz bewirkt sie eine Impulsänderung und somit eine beschleunigte Bewegung