1.6 Beispiele

B1.2: Berechnen Sie die Beschleunigung auf der Oberfläche der Erde unter der Voraussetzung, dass die Masse der Erde homogen und kugelförmig verteilt ist (R: Erdradius).

Mit 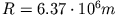und 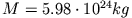ergibt sich

B1.3: Wie groß ist g auf der Mond-, Mars- oder Jupiter-Oberfläche ?

	R	M	g
Mond
Mars
Jupiter

Tablle 1.2 Zum Vergleich von Gravitationsbeschleunigungen

Während unser Gewicht (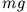) auf dem Mond nur ca. 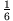des Gewichtes auf der Erde beträgt, würden wir auf dem Jupiter mit dem 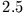fachen Gewicht hart geprüft.

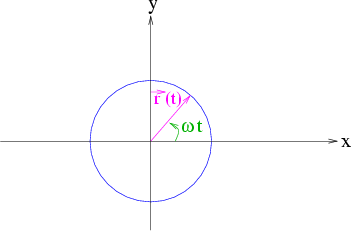
B1.4: Betrachten Sie einen Massenpunkt auf einer Kreisbahn mit Winkelgeschwindigkeit 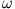. Der Ortsvektor des Massenpunktes lässt sich in Parameterdarstellung angeben

Berechnen Sie 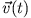und .

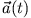Abbildung 1.8: Kreisbahn

Die Geschwindigkeit des Massenpunktes erhalten wir durch Differentiation des Ortsvektors nach der Zeit

Den Betrag der Geschwindigkeit erhalten wir nach Pythagoras aus der x- und y-Komponente

Die Richtung von 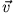steht immer senkrecht auf 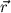, wie man mit Hilfe des Skalarprodukts nachweisen kann (zwei Vektoren stehen senkrecht aufeinander, wenn ihr Skalarprodukt verschwindet. Das Skalarprodukt von 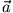und 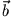berechnet sich nach der Regel

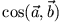ist der zwischen 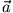und 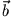eingeschlossene Winkel).
Damit ergibt sich

Für die Beschleunigung gilt

Die Beschleunigung auf einer Kreisbahn ist dem Ortsvektor entgegen- und auf das Kraftzentrum hin gerichtet.

B1.5: Ein Kommunikationssatellit bewege sich synchron zur Erde in der Äquatorebene. Wie weit muss der Satellit von der Erdoberfläche entfernt sein, damit er geostationär ist ?

Der Satellit bewegt sich auf einer Kreisbahn um die Erde. Die Bewegungsgleichung des Satelliten ist

Für die Kreisbahn haben wir im vorigen Beispiel gefunden

Kreisfrequenz 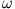und Umlaufzeit 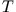sind durch 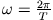verknüpft, so dass wir erhalten

(Beachten Sie, dass wir beiläufig das 3. Keplersche Gesetz erhalten haben

Somit ergibt sich bei einer Umlaufzeit 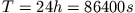(geostationär bedeutet, dass der Satellit immer über dem selben Punkt der Erdoberfläche ''steht'')

Dies ist der Abstand zum Erdmittelpunkt. Die Höhe des Satelliten bezogen auf die Erdoberfläche ist dann

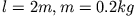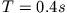B1.6: Ein Kind wirbelt ein Seil der Länge l an dessen Ende eine Masse m befestigt ist horizontal über seinem Kopf. Die Umlaufzeit der Masse betrage T Sekunden. Bestimmen Sie für und a) die Scheinkraft entlang des Seils und b) mit welcher Geschwindigkeit die Masse tangential wegfliegen würde, falls das Seil reißt.

Zu a)

Dazu im Vergleich die Gravitationskraft

Zu b) Für die Kreisbahn gilt 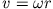und somit