Die Lösung des Gleichungssystems erfolgt am sichersten mit
der Cramerschen Regel:
Sei
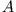 eine
eine 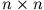 Matrix mit
Matrix mit
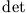
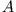
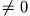 und
und
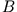
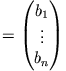 eine
einspaltige Matrix (Vektor), gilt für die Lösung
eine
einspaltige Matrix (Vektor), gilt für die Lösung
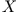
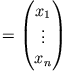 des Gleichungssystems
des Gleichungssystems
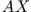

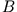 :
wenn
:
wenn
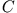
 diejenige Matrix ist,
die entsteht, wenn man in
diejenige Matrix ist,
die entsteht, wenn man in
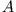 die i-te Spalte durch
die i-te Spalte durch
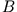 ersetzt.
Zur Klassifikation der möglichen Lösungen untersuchen wir
die Determinante der Matrix
ersetzt.
Zur Klassifikation der möglichen Lösungen untersuchen wir
die Determinante der Matrix
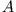 .
.
- a)
- Für
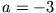 (eine der beiden Lösungen von
(eine der beiden Lösungen von
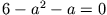 )
kann das Gleichungssystem zu einem Widerspruch geführt werden, indem die erste Gleichung mit 3
multipliziert und von der zweiten Gleichung abgezogen wird. Das widerspricht nun Gleichung 3,
folglich existiert gar keine Lösung.
)
kann das Gleichungssystem zu einem Widerspruch geführt werden, indem die erste Gleichung mit 3
multipliziert und von der zweiten Gleichung abgezogen wird. Das widerspricht nun Gleichung 3,
folglich existiert gar keine Lösung.
- b)
- Für
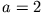 ist die zweite Gleichung offensichtlich die
Summe der ersten und dritten Gleichung und damit linear abhängig und das
Gleichungssystem ist unterbestimmt. Die beiden verbleibenden Gleichungen
ist die zweite Gleichung offensichtlich die
Summe der ersten und dritten Gleichung und damit linear abhängig und das
Gleichungssystem ist unterbestimmt. Die beiden verbleibenden Gleichungen
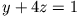 und
und
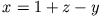 lassen
lassen 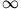 -viele Lösungen zu, da zu
jedem
-viele Lösungen zu, da zu
jedem 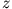 -Wert ein Wertepaar
-Wert ein Wertepaar 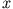 und
und 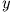 gefunden werden kann, das die Gleichungen erfüllt.
gefunden werden kann, das die Gleichungen erfüllt.
- c)
- Eine eindeutige Lösung existiert, falls
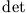
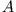
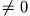 ist, also
für
ist, also
für 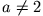 und
und 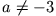 .
.
H.J. Lüdde, M. Keim
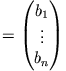 eine
einspaltige Matrix (Vektor), gilt für die Lösung
eine
einspaltige Matrix (Vektor), gilt für die Lösung
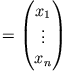 des Gleichungssystems
des Gleichungssystems