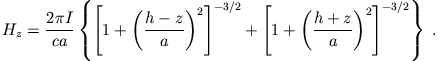Das Magnetfeld eines vom Strom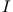 
durchflossenen Kreisringes (Radius 
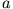) ist nach Biot-Savart gegeben durch:
Mit
und
findet man auf der z-Achse (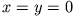
):
Ausgangspunkt zur Lösung der Aufgabe ist das obige Ergebnis, dass das Magnetfeld eines Stromkreises um die
z-Achse nur eine Komponente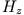 
auf dieser Achse besitzt, nämlich
wenn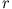 
den Abstand vom Mittelpunkt des Stromkreises bezeichnet (vorher 
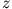). Am Punkt P der
Abbildung ist dieser Abstand 
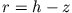für den oberen und 
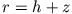für den unteren Ring.
Daher wird dort
Wir betrachten nun die Umgebung des Mittelpunktes und führen die folgenden Abkürzungen ein
Dann wird
Entwicklung nach Potenzen von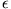 
bis einschließlich
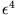ergibt mit
zunächst
Fügt man den entsprechenden zweiten Term der Gleichung für 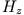hinzu, so fallen die
ungeraden Potenzen von 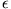heraus und die geraden treten zweimal auf. Das führt auf
Ein Optimum an Feldhomogenität in der Umgebung der Stelle
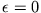erhalten wir offenbar, wenn der
Faktor von
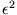verschwindet, also fü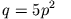r
 oder |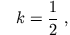
|
wenn also der Abstand der beiden Ringe voneinander (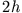
) gleich ihrem Radius 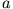wird. Das ist die
Helmholtzsche Bedingung. Der Faktor von
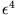wird in diesem Falle
so dass wir für die Feldstärke
erhalten.
Anmerkung: Eine genauere Untersuchung des Feldes zeigt, dass die radiale Komponente senkrecht
zur z-Achse proportional zur dritten Potenz des Abstandes wird. Für eine praktische Anwendung muss man
auch über die endlichen Abmessungen der Spulenkörper integrieren.
M.Keim, H.J. Lüdde
