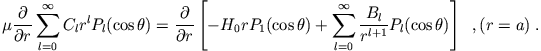5

Im ganzen Raum gilt

Diese Gleichungen sind mit der Randbedingung

zu lösen. Aus der ersten Gleichung folgt, dass 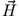die Darstellung

mit einem skalaren Potential 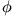besitzt. Innerhalb und außerhalb der Kugel (aber nicht auf dem Rand) gilt dann (nach der zweiten Gleichung)

Lösungsidee: Mache einen allgemeinen Ansatz für 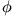und bestimme die auftretenden Koeffizienten durch die Randbedingung und die Anschlussbedingung der beiden Felder auf der Kugeloberfläche. Die allgemeinste Lösung von 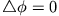, die am Ursprung nicht divergiert und rotationssymmetrisch bezüglich der z-Achse ist, lautet:

a)

Randbedingung für :

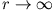Das bedeutet

Sortiert man diesen Ausdruck nach einzelnen 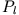, so lassen sich deren Koeffizienten (wegen der linearen Unabhängigkeit der 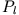) gleich Null setzen. Das führt auf

b)

Anschlussbedingung für die Normalkomponente des 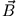-Feldes (Normalkomponente des Gradienten in Kugelkoordinaten: )

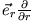Dies führt auf

Analoges Vorgehen zu a) führt auf die Gleichungen

c)

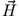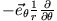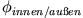Anschlussbedingung für die Tangentialkomponente des -Feldes (Tangentialkomponente des Gradienten in Kugelkoordinaten: - hat nur eine -Komponente, da nicht von 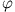abhängen)

Anders ausgedrückt gilt

Dabei ist 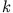eine beliebige Konstante, die nicht von 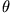abhängt. Einsetzen der Entwicklung für 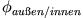liefert

was auf die Gleichungen

führt.

d)

Vergleiche die beiden Gleichungssysteme in b) und c). Es folgt

Also kann die Lösung in der Form

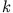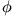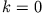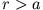geschrieben werden. Es wurde so gewählt, dass an der Kugeloberfläche stetig ist (). Das Magnetfeld für ist also eine Überlagerung eines konstanten Feldes 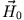und dem Magnetfeld eines magnetischen Dipols mit dem Dipolmoment