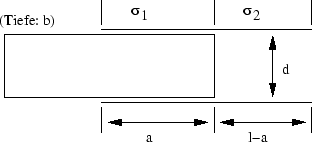
Bezeichnen wir das linke Stück der Länge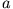 
mit 1, das rechte der Länge 
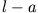mit 2, so wird
und die unveränderte Gesamtladung der Platten
Da jede Platte eine Äquipotentialfläche ist, muss die Potentialdifferenz zwischen beiden in 1 und 2 gleich sein,
also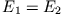 
und
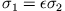. Setzen wir diese Beziehungen in die obigen ein und führen die
gesamte Fläche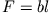 
ein, so erhalten wir
Die elektrische Feldstärke folgt zu
die Potentialdifferenz zu
und schließlich die Kapazität aus
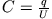zu
Schließlich können wir die Energie des Feldes aus
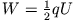entnehmen,
Alle Formeln gehen für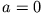 
(kein Dielektrikum) und 
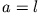(volles Dielektrikum) in die Ausdrücke des entsprechenden Faraday'schen
Grundversuches über.
M.Keim, H.J. Lüdde
