4

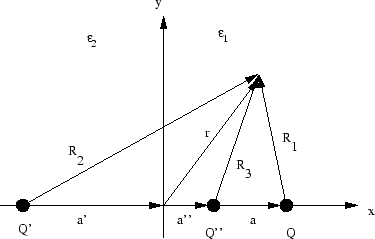
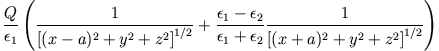Das Potential im Halbraum 1 wird durch 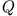und die Spiegelladung 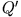bestimmt, das Potential im Halbraum 2 durch die Scheinladung 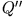. Ansatz: 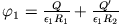; 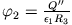Motivation: Man versucht die Potentiale in den beiden Halbräumen mit Scheinladungen so zu konstruieren, als enthielte der ganze Raum nur ein Dielektrikum 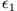bzw. .

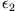Randbedingungen

1)

Das Potential an der Grenzfläche 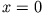muss stetig sein

Daraus folgt unmittelbar

2)

Da auf der Grenzfläche keine Flächenladungen existieren dürfen, muss wegen

auch die Ableitung die Bedingung

erfüllen. Somit folgt

Annahme: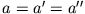
Lassen sich beide Bedingungsgleichungen unter dieser Annahme erfüllen, d.h. erfüllt unter dieser Annahme das Potential beide Randbedingungen, so ist die Annahme automatisch gerechtfertigt, denn die Lösung muss ja eindeutig sein.

aus 1)

aus 2)

Es ergibt sich also: