Der Strom erzeugt ein Magnetfeld in Richtung der z-Achse. Dies erzeugt nach dem Induktionsgesetz seinerseits ein elektrisches Ringfeld
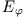 und damit eine Stromdichte
und damit eine Stromdichte
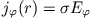 in dem Zylindermetall der Leitfähigkeit
in dem Zylindermetall der Leitfähigkeit 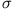 . Dieser Vorgang
wird beschrieben durch die Maxwell-Gleichungen
. Dieser Vorgang
wird beschrieben durch die Maxwell-Gleichungen
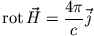 |
(1) |
und
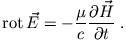 |
(2) |
In Gleichung (1) wurde dabei der Verschiebestrom
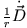 vernachlässigt. Das ist erlaubt, solange
vernachlässigt. Das ist erlaubt, solange
oder aber
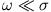 bleibt. Da die metallische Leitfähigkeit
bleibt. Da die metallische Leitfähigkeit 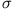 von der Größenordnung
von der Größenordnung 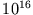
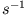 ist, wird diese
Beziehung gut erfüllt, solange
ist, wird diese
Beziehung gut erfüllt, solange 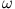 weit unterhalb von Röntgenfrequenzen bleibt.
Mit
weit unterhalb von Röntgenfrequenzen bleibt.
Mit
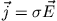 können wir in Gleichung (2)
können wir in Gleichung (2) 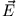 durch
durch 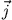 ersetzen:
ersetzen:
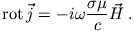 |
(3) |
Mit Hilfe von (1) folgt daraus durch Rotationsbildung
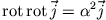 |
(4) |
mit der Abkürzung
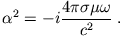 |
(5) |
Nach Lösung der Differentialgleichung (4) können wir dann aus Gleichung (3) das Magnetfeld
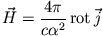 |
(6) |
entnehmen. Da  nur eine Komponente
nur eine Komponente
 besitzt, hat
besitzt, hat 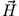 nur eine Komponente
nur eine Komponente 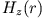 . Daher reduzieren sich die
Gleichungen (4) und (6) auf
. Daher reduzieren sich die
Gleichungen (4) und (6) auf
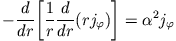 |
(7) |
und
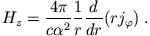 |
(8) |
In ausführlicher Schreibweise lautet Gleichung (7)
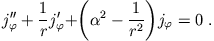 |
(9) |
Das ist eine Besselsche Differentialgleichung, deren bei 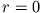 reguläre Lösung
reguläre Lösung
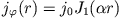 |
(10) |
ist. Daraus leiten wir mit Hilfe von Gleichung (8) für das Magnetfeld
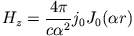 |
(11) |
ab. Die Konstante 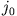 bestimmen wir aus der Forderung, dass an der Oberfläche
bestimmen wir aus der Forderung, dass an der Oberfläche 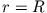 des Metallzylinders das Magnetfeld den Wert
des Metallzylinders das Magnetfeld den Wert
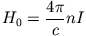 |
(12) |
haben muss. Vergleich von (11) bei 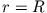 und (12) ergibt
und (12) ergibt
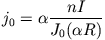 |
(13) |
und daher die Endformeln
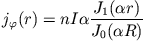 |
(14) |
und
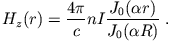 |
(15) |
Die Bessel-Funktionen haben nach (5) ein komplexes Argument,
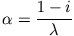 |
(16) |
mit der charakteristischen Länge
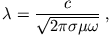 |
(17) |
die ähnlich auch in der Theorie des Skineffektes auftritt (beachte beim Vergleich mit (5):
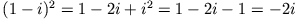 ).
Für
).
Für
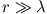 können wir asymptotische Darstellungen verwenden.
Eine entsprechende Rechnung ergibt für den Wirbelstrom
können wir asymptotische Darstellungen verwenden.
Eine entsprechende Rechnung ergibt für den Wirbelstrom
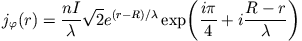 |
(18) |
und für das Magnetfeld
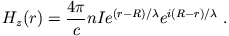 |
(19) |
Die Gleichungen (18) und (19) besagen, daß die Wirbelströme vorwiegend in einer Oberflächenschicht der Dicke 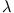 fließen und das
Magnetfeld aus dem Inneren in diese Oberflächenschicht verdrängen. Der Phasenfaktor
fließen und das
Magnetfeld aus dem Inneren in diese Oberflächenschicht verdrängen. Der Phasenfaktor
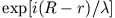 gekoppelt mit der
Zeitabhängigkeit von
gekoppelt mit der
Zeitabhängigkeit von 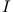 wie
wie
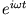 bedeutet, dass
bedeutet, dass 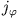 und
und 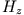 mit der Geschwindigkeit
mit der Geschwindigkeit
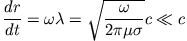 |
(20) |
ins Innere des Zylinders eindringen. Bei 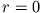 ist nach (14)
ist nach (14)
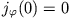 , aber das Magnetfeld behält einen endlichen, wenn auch
kleinen Wert.
, aber das Magnetfeld behält einen endlichen, wenn auch
kleinen Wert.
M.Keim, H.J. Lüdde