Mit der Zeitabhängigkeit der Felder
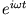erhält man aus den Maxwell-Gleichungen die Beziehungen:
Bildet man die Rotation der ersten beiden Gleichungen und berücksichtigt die unteren beiden Gleichungen, so erhält man die separierten
Wellengleichungen (
)
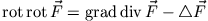Die längs des Rohres laufenden Wellen hängen von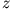 
wie
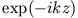ab. Damit lauten die zu lösenden Gleichungen in kartesischen
Koordinaten
- a)
- TE-Wellen (
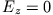), zu lösen ist (
):
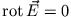Die Randbedingungen in kartesischen Koordinaten sind:
Die Lösungen der Wellengleichung für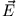 
lauten daher
mit
Die Grenzfrequenz ist somit
Die magnetische Feldstärke folgt nun aus
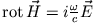zu
Das Magnetfeld erfüllt die Randbedingungen
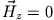, d.h.
- b)
- TM-Wellen (
):
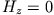Da 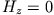beginnt man die Rechnung mit 
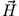. Der Lösungsweg verläuft ansonsten parallel. Man erhält
und aus
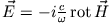
M.Keim, H.J. Lüdde
für
und
und
