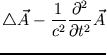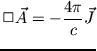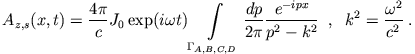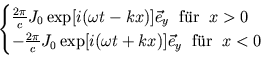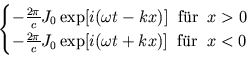7

Die Felder 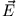und 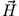kann man aus den Potentialen ( 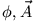) berechnen, die den Wellengleichungen (d'Alembert-Operator: )

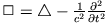genügen, mit

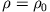folgt aus (Kontinuitätsgleichung). Die allgemeine Lösung der Wellengleichung hat die Form

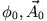( ) sind Lösungen der homogenen Wellengleichung und ( 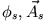) spezielle Lösungen der inhomogenen Wellengleichung. Für die angegebene Stromdichte existiert nur die z-Komponente von 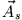, die durch die Translationsinvarianz in der y-z-Ebene lediglich von der x-Koordinate und von der Zeit abhängt

Ansatz:

Mit der Fourierdarstellung der 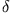-Funktion

liefert dies

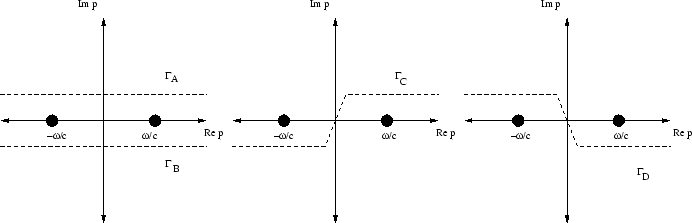
Die Funktion 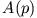hat Pole bei 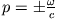. Bei der Ausführung des Fourierintegrals sind diese durch Deformation des Integrationsweges geeignet zu umgehen. Das Integral

kann durch Anwendung des Residuensatzes berechnet werden, wofür die Kontur aber noch zu schließen ist. Entsprechend dem Verhalten der Exponentialfunktion ist die Kontur für 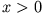in der unteren Halbebene bzw. für 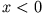in der oberen Halbebene zu schließen (vergleiche mit der Diskussion der zeitabhängigen Greensfunktion).

Man erhält

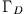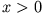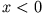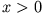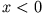und entsprechendes für . Lösung A bzw. B beschreibt eine stehende Welle für bzw. , Lösung C beschreibt eine Welle, die sich für und von der Wand wegbewegt. Die Lösung für 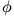erhält man analog. Die Felder erhält man aus ()

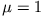Setzt man 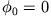und 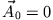, so erhält man z.B. im Falle C