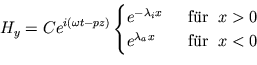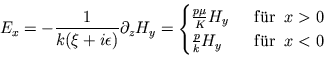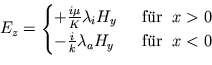Wir setzen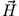 
und 
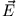proportional zu
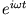an; dann lauten die beiden Ausgangsgleichungen
(mit
,
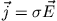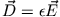und
)
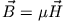Mit den Abkürzungen
dann entsprechend
Das Kabel, dessen Oberfläche die y-z-Ebene ist, soll in z-Richtung von einem hochfrequenten Wechselstrom durchflossen werden.
Das Feld zerfällt in ein TM-System mit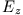 
, 
, 
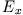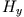und ein TE-System mit 
, 
, 
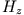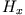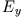. Die Ausgangsgleichungen
lauten in kartesischen Komponenten
und
Wegen des Verschwindens aller Ableitungen nach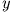 
zerfallen diese Gleichungen in das TM-System
und das TE-System
Wir verfolgen nur das TM-System weiter. Hier gestatten die Gleichungen (1) und (2) die Berechnung der elektrischen Feldkomponenten aus 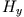. Setzt man
sie in (3) ein, so entsteht für 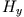die Differentialgleichung
 |
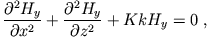(4) |
in der
bedeuten. Gleichung (4) gilt in dieser Form für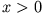 
, also im Inneren des Leiters. Außerhalb, für 
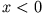, ist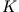 
in (4) durch 
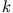zu
ersetzen. Wir suchen nun Lösungen von (4) , die für
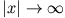verschwinden und bei 
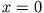stetig sind. Diese Lösungen lauten
mit
Damit die in z-Richtung fortschreitende Welle gedämpft ist, muss außerdem
Im |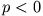
|
werden. Die aus (1) und (3) folgenden Komponenten der elektrischen Feldstärke werden jetzt
 |
|
|
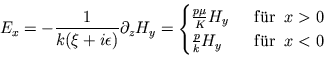(5) |
und
 |
|
|
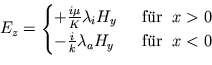(6) |
Die Stromdichte senkrecht zur Oberfläche ist
im Inneren, während außerhalb nur der Verschiebungsstrom
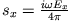existiert. Mit den Werten von (5) mit stetigem
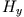bei 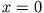sieht man sofort, dass dort beide Größen übereinstimmen, der Strom also stetig durch die Oberfläche hindurchtritt. Die
Stetigkeit der Tangentialkomponente 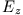führt nach (6) auf
woraus mit den Definitionen für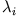 
und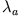 
folgt.
M.Keim, H.J. Lüdde
