Wie in der vorhergehenden Aufgabe können wir die Differentialgleichung
mit
für die Wirbelstromdichte 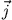 und die Formel
und die Formel
für das magnetische Feld zugrundelegen.
Bei dieser Anordnung der beiden Leiter erzeugen die in z-Richtung fließenden Ströme 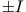 ohne Metallblock das homogene
Magnetfeld
ohne Metallblock das homogene
Magnetfeld
in x-Richtung in dem Bereich
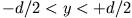 zwischen den beiden Blättern der Breite
zwischen den beiden Blättern der Breite 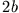 . Dieses magnetische Wechselfeld erzeugt nach dem
Induktionsgesetz ein elektrisches Feld
. Dieses magnetische Wechselfeld erzeugt nach dem
Induktionsgesetz ein elektrisches Feld 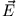 , das den Wirbelstrom der Dichte
, das den Wirbelstrom der Dichte
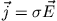 hervorruft. Wie in der vorigen
Aufgabe hat
hervorruft. Wie in der vorigen
Aufgabe hat 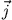 die Richtung der primären Ströme (dort
die Richtung der primären Ströme (dort 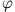 , hier
, hier 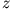 ) und sowohl
) und sowohl 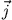 als auch
als auch 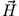 hängen vom Abstand
von den Leitern ab (dort
hängen vom Abstand
von den Leitern ab (dort 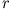 , hier
, hier 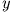 ). Wir erhalten daher ein Magnetfeld
). Wir erhalten daher ein Magnetfeld 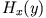 und eine Stromdichte
und eine Stromdichte 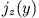 . Dann vereinfacht sich
die obige Gleichung für
. Dann vereinfacht sich
die obige Gleichung für 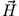 zu
zu
und die Differentialgleichung entsprechend zu
Die Lösung
führt auf
Sie erfüllt die Randbedingung
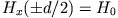 , wenn
, wenn
gesetzt wird. Damit können wir die Lösung in der Form
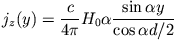 |
(1) |
und
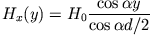 |
(2) |
aufschreiben. Hier ist noch der komplexe Parameter 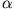 verwendet. Zerlegen wir ihn in Real- und Imaginärteil, so wird
verwendet. Zerlegen wir ihn in Real- und Imaginärteil, so wird
Setzen wir wie in der vorhergehenden Aufgabe wieder
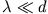 voraus, so fließen die Wirbelströme vorwiegend in einer dünnen Oberflächenschicht der
Dicke
voraus, so fließen die Wirbelströme vorwiegend in einer dünnen Oberflächenschicht der
Dicke 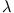 , in der auf der Seite positiver
, in der auf der Seite positiver 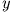
wird. Die Gleichungen (1) und (2) können daher für 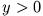 genähert
genähert
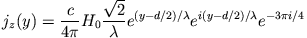 |
(3) |
und
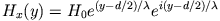 |
(4) |
geschrieben werden. Entsprechendes gilt für negative 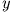 : Nach Gleichung (1) hat
: Nach Gleichung (1) hat 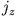 dort das entgegengesetzte, und nach (2)
dort das entgegengesetzte, und nach (2)
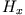 das gleiche Vorzeichen. Beachten wir, dass
das gleiche Vorzeichen. Beachten wir, dass 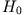 wie
wie 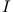 proportional zu
proportional zu
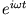 ist, so enthalten beide Formeln
einen Phasenfaktor
ist, so enthalten beide Formeln
einen Phasenfaktor
Das bedeutet eine Eindringgeschwindigkeit der Felder ins Innere des Metallblocks, die
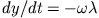 ist, wie in Gleichung (20)
der vorherigen Aufgabe.
ist, wie in Gleichung (20)
der vorherigen Aufgabe.
M.Keim, H.J. Lüdde