Die Lösung
beschreibt stationäre Quellen des elektromagnetischen Feldes, nämlich stationäre Raumladungen als Quellen elektrostatischer Felder und stationäre Ströme als Quellen magnetostatischer Felder.
5.1 Elektrostatische Felder
Die Feldgleichungen der Elektrostatik lauten für isotrope, lineare Medien (
)
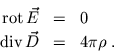
Sie lassen sich zu einer Potentialgleichung, der Poisson Gleichung
zusammenfassen, die unter gegebenen Dirichlet oder Neumann Randbedingungen zu lösen ist.
Je nach Aufgabenstellung ergeben sich verschiedene Lösungsmuster
zur Bestimmung elektrostatischer Felder:
- Das Feld eines Systems von Punktladungen:
Wegen des Superpositionsprinzips können wir das Feld als Überlagerung von Coulombfeldern schreiben
- Keine Raumladungen im betrachteten Volumen V:
Das Feld ergibt sich ausschließlich aus den Randbedingungen, d.h. aus der Vorgabe von Potential (Dirichlet) oder Feld (Neumann) auf der geschlossenen Grenzfläche, die das endliche Lösungsvolumen umschließt. In diesem Volumen löst man die Laplace Gleichung
in Koordinaten, die der Geometrie der Randbedingung angepasst sind.
Lösungsschritte:
- Separationsansatz
- Fundamentalsystem der resultierenden gewöhnlichen Differentialgleichungen (i.a. Spezielle Funktionen)
- Fundamentalsystem der Laplace Gleichung (allgemeine Lösung)
- Bestimmung der Koeffizienten durch Einsetzen der Randbedingungen.
- Raumladungen vorhanden:
- Keine endlichen Grenzflächen im Volumen:
Die allgemeine Lösung der Poisson Gleichung lautet
Berechnung des Integrals in Multipolentwicklung, d.h. Entwicklung der Green Funktion
in den der Symmetrie der
Ladungsverteilung 
angepassten Koordinaten.
- Endliche Grenzflächen im Volumen:
Die allgemeine Lösung der Poisson Gleichung erhält man mit Hilfe von Green Funktionen entsprechend Dirichlet'schen oder Neumann'schen Randbedingungen.(i) Dirichlet'sche Randbedingung: Vorgabe des Potentials
auf der Randfläche 
:
Typische Randbedingung für leitende Oberflächen: in diesem Fall ist das Potential auf der Oberfläche konstant und kann vor das Integral gezogen werden!(ii) Neumann'sche Randbedingung: Vorgabe der Normalkomponente des Feldes
auf der
Randfläche. Nach dem Gauß'schen Gesetz ist dies äquivalent zur
Vorgabe der entsprechenden Oberflächenladung
: Größe der Randfläche,
: über die
Randfläche gemitteltes Potential.
- Keine endlichen Grenzflächen im Volumen:
5.2 Magnetostatische Felder
Die Feldgleichungen der Magnetostatik lauten
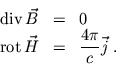
Man kann sie mit Hilfe der Materialgleichung
auf verschiedenen Wegen lösen.
- Dia- und Paramagnetika:
Für lineare, isotrope Medien sind
- und 
Felder
zueinander proportional, d.h.
. Man unterscheidet
Diamagnetika (
) von Paramagnetika (
).
- Vektorpotential für allgemeine Probleme:
Mit
erhält man in Coulombeichung
(
)
Die Vektor Poisson Gleichung wird komponentenweise gelöst analog zu entsprechenden Problemen der Elektrostatik. - Magnetisches Skalarpotential für
:
Da
, existiert ein magnetisches Skalarpotential, so dass
. Mit
erhält man eine Laplace Gleichung für das magnetische Skalarpotential.
- Vektorpotential für allgemeine Probleme:
- Harte Ferromagnetika:
Bei einem harten Ferromagnetikum geht man davon aus, dass die Magnetisierung
unabhängig vom äußeren Magnetfeld ist.
- Vektorpotential für allgemeine Probleme:
In Coulombeichung erhält man für die Vektor Poisson Gleichung
mit dem Magnetisierungsstrom
Die allgemeine Lösung der Poisson Gleichung ist in diesem Fall
Die Felder erhält man aus
- Magnetisches Skalarpotential für :
Bei Abwesenheit wahrer Ströme ist die Poisson Gleichung für das magnetische Skalarpotential
zu lösen. Die allgemeine Lösung ist
Die Felder erhält man aus
- Vektorpotential für allgemeine Probleme:
H.J. Lüdde