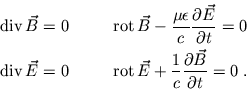
Dabei hat man zusätzlich angenommen, dass das Medium ein idealer Isolator ist (
). D.h. man verliert keine Feldenergie in Form von Joul'scher Wärme:
Die zu den Maxwell Gleichungen korrespondierende Welle wird also ungedämpft
durch das Medium bleiben. Die vier Maxwell Gleichungen lassen sich wieder zu zwei
Wellengleichungen kombinieren
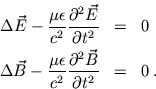
Die homogenen Wellengleichungen für die Felder sind äquivalent zu den Maxwell Gleichungen und entsprechen der allgemeinen Form
die wir bereits für die Potentiale kennen gelernt haben. Die Ausbreitungsgeschwindigkeit
ist typisch für das Medium
wobei das Verhältnis der Ausbreitungsgeschwindigkeiten in Vakuum und Medium als Brechungsindex
interpretiert wird.
Eine Lösung der Wellengleichung ist die ebene Welle
unter der Voraussetzung, dass Wellenzahl und Frequenz die Dispersionsrelation
erfüllen. Man nennt ein Medium dispersionsfrei, wenn
und damit 
unabhängig
von der Frequenz 
sind. Die allgemeine Lösung der Wellengleichung
ist ein Wellenpaket der Form
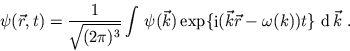
Jetzt erkennt man auch, was der Begriff Dispersion bedeutet: Jede ebene Wellenkomponente besitzt ihre eigene Geschwindigkeit
. Ist diese Geschwindigkeit
frequenzabhängig, d.h. liegt ein dispergierendes Medium vor, so breiten sich die
einzelnen Fourierkomponenten unterschiedlich schnell aus und es muss zu einem
Auseinanderlaufen (dispergieren) des Wellenpaketes kommen.
Eine monochromatische elektromagnetische Welle wird in den beiden Feldkomponenten
und 
durch eine ebene Welle bestimmt
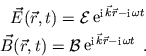
Die Eigenschaften der Amplituden erhält man aus den 'Divergenzgleichungen': sie legen die Geometrie des elektromagnetischen Feldes fest
D.h. E- und B- Feld stehen senkrecht auf der Ausbreitungsrichtung
als
Konsequenz der Quellenfreiheit des Mediums: die elektromagnetischen Wellen sind
also Transversalwellen. Die 'Rotationsgleichungen' liefern einen zusätzlichen
Zusammenhang zwischen den Feldamplituden
d.h. die Feldamplituden stehen ebenfalls senkrecht aufeinander. Solange der Brechungsindex und damit der Wellenvektor
reell sind, besitzen
die Feldamplituden die gleiche Phase. Definiert man die zueinander senkrechten
Vektoren
, kann man diese Eigenschaften
zusammenfassen zu
Dieser Spezialfall entspricht einer monochromatischen linear polarisierten Welle. Drehen sich die Feldamplituden, so spricht man von einer zirkular polarisierten Welle.
H.J. Lüdde