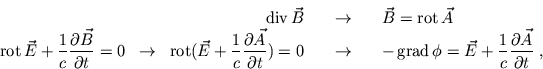
deren Dynamik man aus den inhomogenen Maxwell Gleichungen bestimmt. Für lineare, isotrope Medien erhält man aus dem Coulomb Gesetz
und aus Amperes Gesetz
Da das Vektorpotential nur bis auf Divergenzen festgelegt ist, wählt man die Lorentzeichung
um eine Entkopplung der Potential Gleichungen zu erhalten
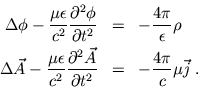
Sie sind äquivalent zu den Maxwell Gleichungen für lineare, isotrope Medien.
Man kann die allgemeine Lösung der inhomogenen Wellengleichung mit Hilfe von
zeitabhängigen Green Funktionen bestimmen. Sei 
die gesuchte Lösung der
Wellengleichung
bezüglich eines beliebigen Quellterms und
die Green
Funktion, die über die Wellengleichung
definiert ist. Durch Einsetzen kann man überprüfen, dass eine Klasse von Green Funktionen durch
gegeben ist, wobei
die Dispersionsrelation des Mediums bedeutet, in dem
sich die elektromagnetische Welle ausbreitet. Für den Fall eines dispersionsfreien
Mediums gilt
unabhängig von der Frequenz und
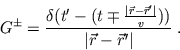
Die allgemeine Lösung ist dann
worin
die Lösung der homogenen Wellengleichung
ist.
ist die physikalisch realisierbare Lösung (
heißt retardierte
Green Funktion), denn sie entspricht dem Kausalprinzip. Ist 
die Zeit, zu der die
Quelle aktiv ist und 
die Zeit, zu der ein Beobachter am Ort 
die 'Konsequenzen'
(Welle) misst, so gilt mit
Demnach kann man die Lösung etwas expliziter schreiben
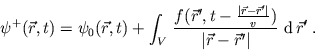
Um zunächst ein paar elementare Ausbreitungsphänomene zu betrachten, wollen wir von einem räumlich lokalen Sender (Quellterm) ausgehen. Weit entfernt von der Quelle 'sieht' man dann nur noch die Ausbreitung der elektromagnetischen Welle als Lösung der homogenen Wellengleichung
unter den gegebenen Anfangs- und Randbedingungen.
H.J. Lüdde