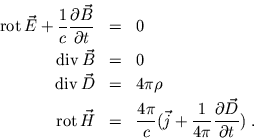
Die Aussagen der beiden homogenen Maxwell Gleichungen legen die Struktur der Felder fest. D.h. (i) man beobachtet keine magnetischen Monopole - das Magnetfeld ist frei von Divergenzen - und (ii) elektrische Wirbelfelder können nur durch zeitlich veränderliche Magnetfelder induziert werden. Elektrostatische Felder sind aufgrund des Zentralkraftcharakters der Coulomb Kraft wirbelfrei.
Die inhomogenen Maxwell Gleichungen initialisieren das elektromagnetische Feld durch
die Feldquellen 
(wahre Ladung), 
(Strom) und
(Verschiebestrom).
Die Einführung des Verschiebestromes durch Maxwell, als Konsequenz der zeitlichen
Änderung des elektrischen Feldes, erlaubt auch im ansonsten quellfreien Raum die
Ausbreitung eines elektromagnetischen Feldes.
Die Maxwell Gleichungen sind nicht lösbar, solange man keine Informationen
über Materialeigenschaften des Mediums besitzt. Die Material Gleichungen
verknüpfen 
und 
bzw 
und 
Felder
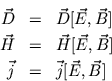
und besitzen i.a. eine komplizierte Funktionalstruktur. Die Material Gleichungen reflektieren die makroskopische Phänomenologie der mikroskopischen Eigenschaften des Mediums, wie z.B. elektrische und magnetische Polarisierbarkeiten oder Ohm'sche Leitfähigkeit. Diese Materialeigenschaften lassen sich nur atomistisch verstehen, also auf der Ebene der Quantentheorie. Für den einfachsten Fall linearer Medien hat man
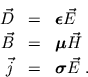
Die Proportionalitätsfaktoren sind i.a. Tensoren, welche die dielektrischen, magnetischen und Ohm'schen Eigenschaften des Mediums beschreiben. Für den Fall isotroper Medien sind
Skalare. I.a. sind die Materialeigenschaften orts- und
zeitabhängig, bzw ihre Fouriertransformierten
abhängig von Frequenz und Wellenlänge einer einfallenden elektromagnetischen Welle.
Als Konsequenz der Maxwell Gleichungen ergeben sich die Grenzbedingungen der Felder
beim Übergang zwischen verschiedenen Medien:
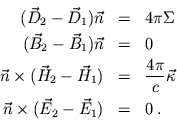
Es bedeuten:
Oberflächenladung und Oberflächenstrom auf der
Grenzfläche zwischen den Medien. Das Verhalten der Normal- bzw Tangentialkomponenten der
Felder ist z.B. verantwortlich für Phänomene der geometrischen Optik (Brechungsgesetze).
H.J. Lüdde