Die Bestimmung der Entfernungen von Himmelsobjekten ist nahezu unmöglich. Fast, aber nicht völlig. Astronomen haben eine große Vielfalt von Techniken entwickelt, von denen hier 26 beschrieben werden. Auf die Bestimmung der Astronomischen Einheit (AE, Maßeinheit für die Größenordnung des Sonnensystems) wird hier nicht eingegangen. Hier geht es nur um Entfernungen außerhalb des Sonnensystems.
Diese Methode verdient das A, denn sie ist der
"Gold"-Standard für astronomische Entfernungen. Sie
basiert auf der Messung zweier Winkel und der dazwischenliegenden
Seite eines Dreiecks, das durch 1. den Stern, 2. die Erde auf der
einen Seite ihrer Umlaufbahn um die Sonne und
3. die Erde sechs Monate später auf der anderen Seite ihres Orbits
gebildet wird. 
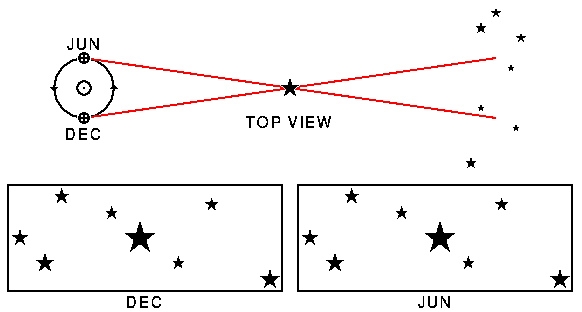
Der obere Teil des obigen Diagramms zeigt die Erde zu zwei verschiedenen Zeiten und das Dreieck, das durch einen nahen Stern und diese zwei Positionen der Erde gebildet wird. Der untere Teil zeigt zwei Bilder dieses nahen Sterns vor dem Hintergrund entfernterer Sterne von den beiden Punkten des Erdorbits aus gesehen. Wenn man durch Schielen die beiden Bilder übereinander projiziert, sieht man entweder in 3-D den nahen Stern vor dem Hintergrund oder man bekommt Kopfschmerzen.
Die Parallaxe eines Sterns ist die Hälfte des Winkels am Stern in obigem Diagramm. Damit ist die Parallaxe gleich dem Winkel am Stern in einem Erde-Sonne-Stern-Dreieck. Da dieser Winkel immer sehr klein ist, bildet der Parallaxenwinkel gemessen in Bogenmaß eine sehr gute Näherung für den Sinus oder den Tangens des Winkels. Somit ist die Entfernung zu einem Stern
D[in cm] = [Entfernung Erde-Sonne in cm]/[Parallaxe in Bogenmaß]
Astronomen nennen die Entfernung Erde-Sonne gewöhnlich 1 Astronomische Einheit mit 1 AE = 1.5E13cm und messen kleine Winkel in Bogensekunden (1.5E13 ist computeresisch für 15000000000000). 1 in Bogenmaß entspricht 648000/pi Bogensekunden. Wenn wir diese Einheiten benutzen, kommen wir zu einer Einheit für die Entfernung von [648000/pi] AE = 3.085678E18 cm = 3.26 Lichtjahre = 1 parsec (= 1 pc). Ein Stern mit einer Parallaxe von 1 Bogensekunde hat die Entfernung von 1 parsec. Kein bekannter Stern hat eine so große Parallaxe. Proxima Centauri hat eine Parallaxe von 0.76" (Anführungszeichen sind das Symbol für Bogensekunden).
Nicht viele Sterne sind nah genug, daß ihre trigonometrische
Parallaxe meßbar wäre. Bei Mitgliedern eines stabilen
Sternhaufens, dessen räumliche Ausdehnung sich nicht ändert,
zum Beispiel bei den Pleiaden,
können die scheinbaren Bewegungen der Sterne des Haufens zur
Bestimmung der Entfernung des Haufens dienen. 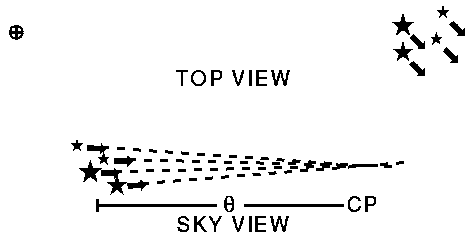
Der obere Teil des obigen Diagramms zeigt die räumliche Bewegung eines Sternhaufens. Beachte, daß die Geschwindigkeitsvektoren parallel sind, sodaß der Haufen weder expandiert noch schrumpft. Wenn wir die Bewegung der Sterne vor dem Hintergrund des Himmels sehen, scheinen sie sich aufgrund perspektivischer Effekte einander anzunähern. Der Winkel zum Konvergenzpunkt heißt hier Theta. Wenn der Haufen sich auf uns zu bewegt, liegt der Konvergenzpunkt hinter dem Haufen, doch dann gibt es einen zweiten Konvergenzpunkt auf der anderen Seite des Himmels, welchen wir benutzen. Über die Eigenbewegung der Sterne vor dem Himmel messen wir Theta und seine Änderungsrate d(Theta)/dt. Zudem benötigen wir die Radialgeschwindigkeit VR des Haufens, die wir mit einem Spektrographen dank des Dopplereffektes messen können. Die Querbewegung des Haufens (VT) kann man mittels VT/VR = tan(Theta) errechnen. Die Entfernung des Sternhaufens beträgt dann
D[in cm] = VT[in cm/s]/[d(theta)/dt]
D[in pc] = (VR/4.74 km/s)*tan(theta)/{d(theta)/dt[in
"/Jahr]}
Die Konstante 4.74 km/s ist eine AE/Jahr. Da ein Zeitintervall von 100 Jahren zur Verfügung steht, um d(Theta)/dt zu messen, sind genaue Entfernungsmessungen naher Sternhaufen möglich. Diese Methode ergibt auf die Hyaden angewendet eine Entfernung von 45.53 +/- 2.64 pc. Der Durchschnittswert der von Hipparcos gemessenen Parallaxen für die Hyadenmitglieder ergibt eine Entfernung von 46.34 +/- 0.27 pc (Perryman et al.).
Eine andere Methode erlaubt die Messung der mittleren Entfernung
einer Gruppe von Sternen, wenn sie alle etwa den gleichen Abstand von
der Erde haben. 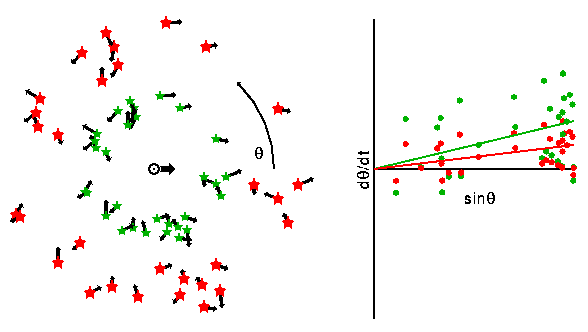
Das obige Diagramm zeigt eine solche Sternengruppe, allerdings mit zwei möglichen Durchschnittsentfernungen. Die grünen Sterne weisen eine geringere mittlere Distanz auf, während die roten Sterne im Mittel weiter entfernt sind. Aufgrund der mittleren Bewegungsgeschwindigkeit des Sonnensystems von 20 km/s relativ zum Durchschnitt der nahgelegenen Sterne stellt man eine mittlere Eigenbewegung der Sterne fest, weg von dem Punkt, auf den sich das Sonnensystem zubewegt. Diesen Punkt nennt man Apex. Sei der Winkel zum Apex hin Theta. Dann wird die Eigenbewegung d(Theta)/dt eine zu sin(Theta) proportionale mittlere Komponente aufweisen, hier verdeutlicht durch die Linien im Graphen (rechts) von d(Theta)/dt gegen sin(Theta). Sei die Steigung dieser Linien my. Dann beträgt die durchschnittliche Entfernung der Sterne
D[in cm] = V(Sonne)[in cm/s]/(my [in Bogenmaß/s]) D[in pc] = 4.16/(my [in "/Jahr])
wobei die Konstante 4.16 die Bewegung des Sonnensystems in AE/Jahr repräsentiert.
Wenn die Radialgeschwindigkeit (VR; derjenige Anteil der Bewegung eines Sterns relativ zur Erde, der genau von der Erde wegweist) der Sterne bekannt ist, kann die Streuung ihrer Eigenbewegungen zur Bestimmung ihrer mittleren Entfernung benutzt werden. Es ist
(Streuung von VR)[in cm/s] D[in cm] = ---------------------------------------- (Streuung von d(theta)/dt)[in Bogenmaß/s]
Das Muster der differentiellen Rotation in unserer Galaxie kann zur Bestimmung der Entfernung einer Quelle benutzt werden, wenn deren Radialgeschwindigkeit bekannt ist.
Die Entfernung zu einem sich ausdehnenden Objekt wie einem Supernova-Rest (zum Beispiel Tycho) kann durch Messung bestimmt werden:
Die Entfernung wird dann so berechnet:
D = VR/d(Theta)/dt mit Theta in Bogenmaß
Ein systematischer Fehler ist dann möglich, wenn die Geschwindigkeit des Materials hinter der Schockwelle geringer ist als die Geschwindigkeit der Schockwelle. In Supernovaresten in der adiabatischen Phase ist das in der Tat der Fall, nämlich VR = 0.75 V(Schockwelle), sodaß die berechnete Entfernung um 25% zu niedrig liegen kann.
Der zentrale elliptische ring um SN1987A in der großen Magellanschen Wolke scheint durch einen kreisförmigen geneigten Ring um den Vorgänger verursacht zu sein. Als der Puls ultravioletten Lichtes von der Supernova den Ring erreichte, leuchtete dieser in ultravioletten Emissionslinien auf, welche durch den International Ultraviolet Explorer (IUE) beobachtet wurden. Der Zeitpunkt des ersten Auftretens dieser Linien, t1, und der Zeitpunkt, als die Linien vom letzten Teil des Rings erglühten, t2, waren beide deutlich in der UV-Lichtkurve des IUE zu erkennen. Wenn t0 der Zeitpunkt des ersten Erscheinens der Supernova ist, beträgt die zusätzliche Zeit für den Weg des Lichts zur Vorder- und Rückseite des Rings:
t1 - t0 = R(1 - sin(i))/c t2 - t0 = R(1 + sin(i))/c
wobei R den Radius des Rings in cm repräsentiert. Damit ist
R = c(t1-t0 + t2-t0)/2
Als das HST (Hubble Space Telescope) in Betrieb genommen wurde, nahm es ein Bild vom SN1987A auf und maß den Beobachtungswinkel des Ringes (Theta). Die Entfernung des Objekt ergibt sich durch den Quotienten:
D = R/Theta mit Theta in Bogenmaß
Auf die große Magellansche Wolke mithilfe von SN1987A angewendet erhält man D = 47 +/- 1 kpc (Gould 1995, ApJ, 452, 189). Diese Methode ist im Grunde die Expansions-Methode angewendet auf die Hülle der Supernova-Strahlung, die sich mit Lichtgeschwindigkeit ausbreitet. Sie kann natürlich auch auf andere bekannte Geometrien angewendet werden.
Wenn die Umlaufbahn eines Begleiters sowohl visuell alsauch
spektroskopisch beobachtbar ist, sind auch die scheinbare und die
tatsächliche Abmessung der Umlaufbahn bekannt. Der Quotient
ergibt die Entfernung.

Die Farben entsprechen etwa Oberflächentemperaturen von 5000, 6000 und 7000 K. Die Farbunterschiede sind relativ gering, doch die Oberflächenhelligkeit variiert stark: in der Tat wurde die Oberflächenhelligkeit hier noch auf die Hälfte reduziert um den kühlen Stern überhaupt sichtbar werden zu lassen. Indem er den Blauanteil des Sternlichts gegenüber seinem Gelb-Grün-Anteil mißt, mißt der Astronom die B-V-Farbe des Sterns. Die Bestimmung des Blauanteil/Visuellanteil-Quotienten kann zur Schätzung der Oberflächenhelligkeit SB eines Sterns verwendet werden. Da der visuelle Strahlungsfluß ebenfalls gemessen wird, ist der Beobachtungswinkel Theta des Sterns bekannt, nämlich theta = sqrt[Strahlungsfluß/(pi*SB)]. Wenn auch der tatsächliche Radius R bestimmt werden kann, beträgt die Entfernung
D = R/Theta mit Theta in Bogenmaß
Die Baade-Wesselink-Methode wird bei pulsierenden Sternen angewendet. Über die Farb- und Strahlungsfluß-Kurven findet man das Verhältnis der Radien zu verschiedenen Zeiten:
sqrt[Strahlungsfluß(t2)/SB(Farbe(t2)] R(t2)/R(t1) = ------------------------------------- sqrt[Strahlungsfluß(t1)/SB(Farbe(t1)]
Dann wird mithilfe aller Spektren des Sterns während einer vollen Pulsationsperiode seine Radialgeschwindigkeit Vr(t) bestimmt. Wenn man weiß, wie schnell die Oberfläche des Sterns sich bewegt, erhält man R(t2)-R(t1) indem man Geschwindigkeit*Zeit während des Zeitintervalls zwischen t1 und t2 addiert. Wenn man nun sowohl den Quotienten der Radien R(t2)/R(t1) von Strahlungsfluß und Farben her kennt und die Differenz der Radien R(t2)-R(t1) durch die Spektroskopie, hat man zwei Gleichungen mit zwei Unbekannten, die man leicht nach den Radien auflösen kann. Über Radius und Beobachtungswinkel erhält man die Entfernung mit D = R/Theta.
Bei einem spektroskopischen Doppellinien-Begleiter findet man die scheinbare Größe der Umlaufbahn a*sin(i) durch die Amplitude der Radialgeschwindigkeit und die Periodendauer. Bei einem verdeckenden Begleiter werden die relativen Radien der Sterne R1/a und R2/a und die Neigung der Umlaufbahn i durch Analyse der Form der Verdeckungs-Lichtkurven ermittelt. Über die mithilfe des beobachteten Strahlungsflusses und der Farben erhaltenen Oberflächenhelligkeit können die Beobachtungswinkel der Sterne geschätzt werden. R1 ergibt sich aus i, a*sin(i) und R1/a; und mit Theta1 bestimmt man die Entfernung.
Die Baade-Wesselink-Methode kann auch auf expandierende Sterne
angewendet werden: die Änderungen des Radius müssen nicht
periodisch sein. Sie wurde bereits auf Typ II-Supernovae
angewendet. Das sind massive Sterne mit wasserstoffreicher Hülle,
die explodiert, wenn der Kern zu einem Neutronenstern kollabiert. Sie
kann auch bei Typ Ia-Supernovae zur Anwendung kommen, doch diese
Objekte haben in ihrem Spektrum keine Wasserstoff-Linien. Da das
Oberflächenhelligkeit/Farbe-Gesetz mithilfe von normalen
wasserstoffreichen Sternen geeicht wird, wird die EP-Methode
normalerweise bei wasserstoffreichen Supernovae vom Typ II
verwendet. Die Typ II SN1987A in der großen Magellanschen Wolke
diente zur Eichung dieses Entfernungs-Indikators.
D = sqrt[Helligkeit/(4*pi*Strahlungsfluß)]
Als man Ende des 19. und Anfang des 20. Jahrhunderts begann die Entfernungen zu nahen Sternen mit Hilfe der trigonometrischen Parallaxe zu bestimmen, wurde auch die Untersuchung der Helligkeit von Sternen möglich. Einar Hertzsprung und Henry Norris Russel trugen die Sterne in einen Graphen mit den Achsen Helligkeit und Temperatur ein. Die meisten Sterne kamen dabei auf einer schmalen Spur zu liegen, die man Hauptreihe nannte, in jenem Diagramm, welches man nach ihren Erfindern H-R-Diagramm benannte. Oft wird heute die absolute Größe anstelle der Helligkeit gebraucht und der Spektraltyp oder die Farbe anstelle der Temperatur.
Wenn man eine Sterngruppe betrachtet, bilden die scheinbaren Größen und Farben der Sterne eine Spur, die parallel zur Hauptreihe ist. Durch korrekte Wahl der Entfernung konvertieren die scheinbaren Größen in absolute Größen, die genau auf der Standard-Hauptreihe liegen.
Wenn das Spektrum eines Sterns sorgfältig beobachtet wird, kann man neben der chemischen Zusammensetzung der Atmosphäre des Sterns noch zwei weitere Parameter bestimmen. Der erste ist die Oberflächentemperatur des Sterns, welche den Spektraltyp des Sterns mittels der Buchstaben OBAFGKM von den heißesten bis zu den kühlsten bestimmt. Die heißen O-Sterne zeigen Linien ionisierten Heliums, die B-Sterne neutrales Helium, die A-Sterne haben starke Wasserstofflinien, die F- und G-Sterne verschiedene Metall-Linien und die kältesten K- und M-Sterne weisen molekulare Bänder auf. Die Spektralklassen sind weiter aufgeteilt durch eine Ziffer, so ist z.B. die Sonne ein G2-Stern.
Der zweite Parameter, der ermittelt werden kann, ist die Oberflächen-Schwerkraft des Sterns. Je höher die Oberflächen-Schwerkraft, desto höher der Atmosphärendruck. Hoher Druck führt zur Verbreiterung der Linien und reduziert das Ausmaß der Ionisation in der Atmosphäre. Die Oberflächen-Gravitation wird durch eine römische Ziffer von I bis V gekennzeichnet, wobei die I die niedrigste und die V die höchste ist (die Klasse VI gilt für weiße Zwerge, die separat klassifiziert werden). Sterne mit hoher Oberflächengravitation (Klasse V) werden Zwerge genannt, während die Sterne mit mittlerer Schwerkraft (Klasse III) Riesen heißen und Sterne mit geringer Schwerkraft (Klasse I) Superriesen. Die Anwendung der Oberflächen-Schwerkraft zur Bestimmung der Helligkeit eines Sterns beruht auf drei Beziehungen:
L = 4*pi*sigma*T4*R2 L = A*Mb Masse-Helligkeits-Gesetz mit b = 3-4 g = G*M/R2
Sind die Temperatur über den Spektraltyp und die Oberflächengravitation über die Helligkeitsklasse ermittelt, können durch diese Gleichungen die Masse und die Helligkeit bestimmt werden. Wenn Helligkeit und Strahlungsfluß bekannt sind, folgt die Entfernung als Umkehrung des Quadrat-Gesetzes.
Eine Warnung zu dieser Methode: sie funktioniert nur bei normalen
Sternen und jedes betrachtete einzelne Objekt könnte unnormal
sein. Der Hauptreihen-Vergleich in einem Sternhaufen ist viel
verläßlicher, da die normalen Sterne in einer
größeren Anzahl von Sternen leichter zu finden sind.
RR Lyrae-Sterne sind pulsierende Sterne wie die Cepheiden, aber von geringer Masse und mit kurzen Perioden (unter einem Tag). Man findet sie in Kugelhaufen und sie scheinen alle dieselbe Helligkeit zu haben. Da die Massen von RR Lyrae-Sternen als Massen von Sternen bestimmt werden, die die Hauptreihe verlassen, könnte diese konstante Helligkeit durch die Altersähnlichkeit innerhalb von Kugelhaufen hervorgerufen werden.
Cepheiden-Veränderliche sind pulsierende Sterne, die nach dem
hellsten Vertreter ihrer Klasse, Delta Cephei, benannt wurden. Diese
Sterne pulsieren, da die Zonen ionisierten Wasserstoffs und Heliums
nahe ihrer Oberfläche liegen. Das stabilisiert mehr oder weniger
die Temperatur des Veränderlichen und produziert einen
Instabilitäts-Streifen im H-R-Diagramm. 
Das obige Diagramm zeigt die Phasen des Sterns, wo er
größer und kühler, dann kleiner und heißer
ist. Cepheiden sind am hellsten, wenn sie am heißesten sind,
nämlich nahe ihrer Minimalgröße. Da alle Cepheiden
ungefähr dieselbe Temperatur haben, bestimmt die Größe
eines Cepheiden ihre Helligkeit. Ein größeres pulsierendes
Objekt hat natürlich eine längere Pulsationsperiode als ein
kleineres desselben Typs. Damit gibt es eine
Perioden-Helligkeit-Relation für Cepheiden. Wenn die Perioden
zweier Cepheiden sich um einen Faktor von zwei unterscheiden, ist der
"langsamere" Cepheide etwa 2.5mal so hell wie der
schnellere. Da die Periode eines Veränderlichen leicht gemessen
werden kann, bieten Cepheiden sich an, die Entfernungen zu Galaxien zu
bestimmen. Weiterhin sind Cepheiden ziemlich hell, sodaß sie
sogar in Galaxien bis hin zum Virgo-Haufen, zum Beispiel im M100 gesehen
werden können. Das einzige Problem mit den Cepheiden ist die
Eichung der Perioden-Helligkeit-Relation, die nur indirekt über
Cepheiden in der Magellanschen Wolke und in Sternhaufen
durchgeführt werden kann, deren Entfernung durch
Hauptreihen-Vergleich bestimmt wird. Zudem hat man zu beachten,
daß die Eichung durch das Vorkommen von Metallen in den
Cepheiden beeinflußt werden kann, welches in der großen
Magellanschen Wolke viel geringer ist als in hellen Spiralgalaxien wie
M100.
Planetarische Nebel sind Sterne, die die Stadien des roten Riesen und des asymptotischen Riesen hinter sich gelassen und ihre Restwasserstoff-Hülle abgestossen haben, welche einen ionisierten Nebel um einen sehr heißen und kleinen Zentralstern herum bildet. Sie senden starke Lichtstrahlung im Bereich der 501nm-Linie des doppelt ionisierten Sauerstoffs (O III) aus, welche sie leicht auffindbar macht. Die hellsten planetarischen Nebel scheinen in vielen Galaxien die gleiche Helligkeit zu haben, sodaß ihr Strahlungsfluß als Entfernungs-Indikator verwendet werden kann. Dies Methode hängt zusammen mit der Oberflächenhelligkeitsfluktuations-Methode, welche bei den asymptotischen Riesen funktioniert, bevor sie ihre Hülle abgestoßen haben.
Wenn eine Galaxie sehr nahe ist, können einzelne Sterne aufgelöst werden. Die Helligkeit dieser Sterne kann zur Schätzung der Entfernung der Galaxie verwendet werden. Oft nimmt man an, daß es eine feste obere Grenze für die Helligkeit von Sternen gibt, doch das scheint eine ungenaue Annahme zu sein. Trotzdem kann, sofern eine große Population heller Sterne untersucht wird, eine vernünftige Entfernungsschätzung möglich sein.
Heiße und helle Sterne ionisieren das Wasserstoffgas um sie herum und erzeugen eine H II-Region wie den Orion Nebel. Der Durchmesser der größten H II-Regionen in Galaxien gilt als Standard-Maß, das zur Bestimmung von Entfernungen benutzt werden kann. Allerdings scheint auch diese Annahme ungenau zu sein.
Wenn eine Galaxie zu fern ist um noch einzelne Sterne auflösen zu können, kann man die Entfernung immer noch über statistische Fluktuationen in der Anzahl der Sterne pro Pixel schätzen. Bei einer nahen Galaxie mögen 100 Sterne in jedes Pixel eines Fotos projiziert werden, während entferntere Galaxien größere Zahlen als 1000 aufweisen dürften. Die nahe Galaxie dürfte +/- 10% Fluktuation in der Oberflächenhelligkeit (1/sqrt(N)) zeigen, während die entferntere bei 3% Fluktuation liegen könnte. Eine Grafik [75 kB] zur Illustration zeigt eine nahe Zwerg-Galaxie und eine Riesengalaxie in einer Entfernung, in der ihr gesamter Strahlungsfluß der gleiche wie der der nahen Zwergin ist. Beachte, daß die entfernte Riesengalaxie ein viel unschärferes Bild zeigt als die nahe Zwergin.
Supernovae vom Typ Ia sind die Explosionen weißer Zwerge in
Doppelsystemen. Materieraub von einem Begleiter hebt die Masse
über das Maximum für stabile weiße Zwerge, das Chandrasekhar-Limit.
Der weiße Zwerg beginnt dann zu kollabieren, doch die
Kompression enzündet ein explosives Kohlenstoff-Brennen, das zur
völligen Vernichtung des Sterns führt. Die ausgesandte
Strahlung bezieht ihre Energie primär aus dem Zerfall
radioaktiven Nickels und Kobalts, die bei der Explosion erzeugt
werden. Die Spitzenhelligkeit korreliert in der Lichtkurve mit der
Zerfallsrate. Nach Anwendung dieser Korrektur kann die relative
Helligkeit einer SN vom Typ Ia innerhalb von 20% Genauigkeit bestimmt
werden. Einige SN Ia haben in genügend nahen Galaxien
stattgefunden, sodaß mit dem Hubble Space Telescope die
absoluten Entfernungen und Helligkeiten mithilfe von
Cepheiden-Veränderlichen bestimmt werden können. Dies
führte zu einer der genauesten Bestimmungen der
Hubble-Konstante.
Die Rotationsgeschwindigkeit einer Spiralgalaxis ist ein Indikator ihrer Helligkeit. Die Relation lautet annähernd
L = Const * V(rot)4
Da die Rotationsgeschwindigkeit einer Spiralgalaxis mit einem
optischen Spektrographen oder einem Radioteleskop gemessen werden
kann, kann die Helligkeit bestimmt werden. Kombiniert mit dem
gemessenen Strahlungsfluß
ergibt diese Helligkeit die Entfernung. Das Diagramm unten zeigt zwei Galaxien:
eine Riesenspirale und eine Zwergspirale, doch die kleine Galaxie ist
näher zur Erde, womit die beiden den gleichen Beobachtungswinkel
am Himmel aufweisen und die gleiche scheinbare Helligkeit. 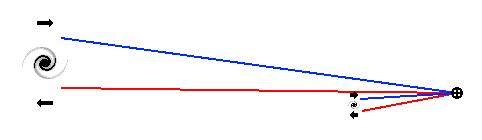
Dafür hat die entfernte Galaxie eine höhere Rotationsgeschwindigkeit, sodaß der Unterschied zwischen der rotverschobenen und der blauverschobenen Seite der entfernten Riesengalaxis höher ausfällt. Auf diese Weise kann die relative Entfernung der zwei Galaxien ermittelt werden.
Die Geschwindigkeitsverteilung der Sterne sigma(v) in einer elliptischen Galaxie ist ein Indikator ihrer Helligkeit. Die Beziehung lautet annähernd
L = Const * sigma(v)4
Da die Geschwindigkeitsverteilung in einer elliptischen Galaxie mit einem optischen Spektrographen gemessen werden kann, kann auch die Helligkeit bestimmt werden. Zusammen mit dem gemessenen Strahlungfluß ergibt dies die Entfernung.
Die hellsten Galaxien in einem Galaxienhaufen
werden als Standardkerzen benutzt. Diese Annahme leidet unter
denselben Schwierigkeiten, welche die Methode der hellsten Sterne und
der größten H II-Regionen plagen: üppige Haufen mit
vielen Galaxien werden wahrscheinlich eher einen Vertreter der
hellsten Galaxien beherbergen, auch wenn diese sehr selten sind,
während sie in kleineren Haufen häufiger ganz fehlen
könnten.
Wenn ein Quasar durch eine Gravitationslinse
betrachtet wird, sind mehrere Bilder zu sehen, wie im folgenden
Diagramm gezeigt. 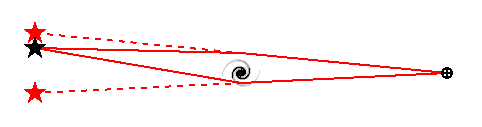
Der Weg des Lichts vom Quasar zu uns, das diese Bilder liefert, hat unterschiedliche Längen, die sich annähernd durch D*[cos(theta1)-cos(theta2)] unterscheiden, wobei Theta der Beugungswinkel und D die Entfernung vom Quasar ist. Da Quasare zeitlich veränderliche Quellen sind, können wir die Weglängen-Differenz messen, indem wir auf zeitverschobene Veränderungen in den mehrfachen Bildern warten. Ende 1996 konnte diese Zeitverschiebung in zwei Quasaren gemessen werden: im originalen double QSO 0957+061, mit dem Ergebnis von Ho = [63 +/- 12] km/s/Mpc, und in PG1115+080 mit einem Resultat von Ho = 42 km/s/Mpc. Eine andere Analyse derselben Daten liefert Ho = [60 +/- 17] km/s/Mpc.
Heißes Gas in Galaxienhaufen verzerrt das Spektrum des
kosmischen Mikrowellenhintergrundes. Das folgende Diagramm zeigt ein
Beispiel für diesen Prozess. Die heißen Elektronen in dem
Galaxienhaufen streuen einen kleinen Teil der Photonen des kosmischen
Mikrowellenhintergrundes und ersetzen sie durch Photonen von etwas
höherer Energie. 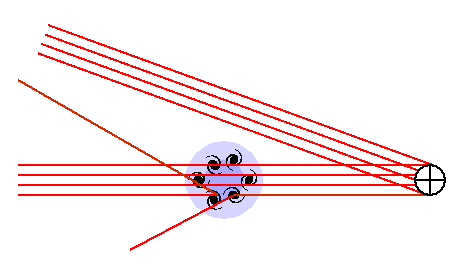
Der Unterschied zwischen dem KMWH betrachtet durch den Galaxienhaufen und dem unmodifizierten KMWH anderswo am Himmel kann gemessen werden. Allerdings werden lediglich etwa 1% der Photonen auf ihrem Weg durch den Galaxienhaufen durch die Elektronen des heißen ionisierten Gases gestreut und die Energie dieser Photonen wird durchschnittlich nur um etwa 2% erhöht. Das führt zu einer Verringerung von Photonen niedriger Energie von ungefähr 0.01*0.02 = 0.0002 or 0.02%, was sich als Verringerung der Temperaturstrahlung um 500 microKelvin zeigt. Bei hohen Frequenzen (höher als ca. 218GHz) scheint der Galaxienhaufen dafür heller als der Hintergrund. Dieser Effekt ist proportional zu 1. der Dichte der Elektronen, 2. der Ausdehnung des Galaxienhaufens in Sichtlinie und 3. der Elektronentemperatur. Der Parameter, der diese Faktoren zusammenfasst, heißt der Kompaneets-y-Parameter, mit y = tau*(kT/mc2). Tau ist die optische Tiefe bzw. der Anteil der gestreuten Photonen, während (kT/mc2) die Elektronentemperatur in Einheiten der Restmasse des Elektrons ist.
Die Röntgen-Strahlung IX vom heißen Gas im Galaxienhaufen ist proportional zu 1. dem Quadrat der Dichte der Elektronen, 2. der Ausdehnung des Haufens in Sichtlinie und hängt 3. von der Elektronentemperatur und der Röngtenstrahlungs-Frequenz ab. Ergebnis ist der Quotient
y2/IX = CONST * (Dicke in Sichtlinie) * f(T)
Wenn wir annehmen, daß die Ausdehnung in Sichtlinie gleich dem Durchmesser des Galaxienhaufens ist, können wir über den scheinbaren Durchmesser (Beobachtungswinkel) die Entfernung berechnen.
Diese Technik ist sehr schwierig. Jahre harter Arbeit durch
Pioniere wie Mark Birkinshaw lieferten nur wenige
Entfernungs-Resultate und Werte für Ho, die zum
unteren Ende hin tendieren. Jüngste Arbeiten an dicht
gebündelten Radio-Interferometern bei 30 GHz ergaben präzise
Messungen der Radio-"Helligkeits"-Verringerung für 18
Galaxienhaufen, aber nur 3 von diesen verfügen über
adäquate Röntgenstrahlungs-Daten.
Die Dopplerverschiebung ist die
Rotverschiebung eines entfernten Objektes und unser bester Indikator
für ihre Entfernung. Aber wir müssen die Hubble-Konstante
kennen.
Doch halt, das war nicht alles! Verteilungsmessungen von Pulsaren und interstellare Auslöschung nehmen mit der Entfernung entlang einer gegebenen Sichtlinie zu und können so zur Entfernungsmessung verwendet werden. Die Helligkeitsfunktion von Kugelhaufen kann zur Schätzung der Entfernung von Galaxien mithilfe der beobachteten Helligkeit ihrer Kugelsternhaufen dienen.
© 1997-1998 Edward L. Wright. Last modified 4-Mar-1998
Übersetzung A.V. Aug.1998 ohne Gewähr