Das Doppelpendel mit Reibung

>    m1:=1:
m2:=1:
l1:=1:
l2:=1:
g:=9.81:
beta:=0.02:

DR:=beta*(l1/2/m1*q1_t^2+l2/2/m2*q2_t^2);
T:=1/2*m1*l1^2*q1_t^2 + 1/2*m2*(l1^2*q1_t^2 + l2^2*q2_t^2 + 2*l1*l2*q1_t*q2_t*cos(q1-q2));
V:=m1*g*(l1+l2-l1*cos(q1)) + m2*g*(l1+l2-(l1*cos(q1) + l2*cos(q2)));
L:=T-V;

DR := .1000000000e-1*q1_t^2+.1000000000e-1*q2_t^2

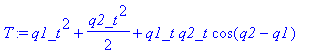
T := q1_t^2+1/2*q2_t^2+q1_t*q2_t*cos(q2-q1)

V := 39.24-19.62*cos(q1)-9.81*cos(q2)

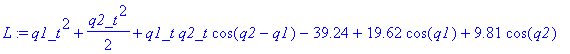
L := q1_t^2+1/2*q2_t^2+q1_t*q2_t*cos(q2-q1)-39.24+19.62*cos(q1)+9.81*cos(q2)

>    EulerLagr1:=diff(subs({q1=q1(t),q1_t=diff(q1(t),t),q2=q2(t),q2_t=diff(q2(t),t)},diff(L,q1_t)),t) - subs({q1=q1(t),q1_t=diff(q1(t),t),q2=q2(t),q2_t=diff(q2(t),t)},diff(L,q1))=
-subs({q1=q1(t),q1_t=diff(q1(t),t),q2=q2(t),q2_t=diff(q2(t),t)},diff(DR,q1_t));
EulerLagr2:=diff(subs({q1=q1(t),q1_t=diff(q1(t),t),q2=q2(t),q2_t=diff(q2(t),t)},diff(L,q2_t)),t) - subs({q1=q1(t),q1_t=diff(q1(t),t),q2=q2(t),q2_t=diff(q2(t),t)},diff(L,q2))=
-subs({q1=q1(t),q1_t=diff(q1(t),t),q2=q2(t),q2_t=diff(q2(t),t)},diff(DR,q2_t));

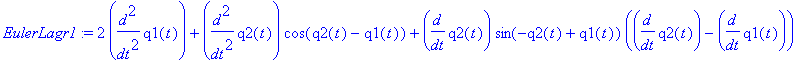
EulerLagr1 := 2*diff(q1(t),`$`(t,2))+diff(q2(t),`$`(t,2))*cos(q2(t)-q1(t))+diff(q2(t),t)*sin(-q2(t)+q1(t))*(diff(q2(t),t)-diff(q1(t),t))-diff(q1(t),t)*diff(q2(t),t)*sin(q2(t)-q1(t))+19.62*sin(q1(t)) = ...
EulerLagr1 := 2*diff(q1(t),`$`(t,2))+diff(q2(t),`$`(t,2))*cos(q2(t)-q1(t))+diff(q2(t),t)*sin(-q2(t)+q1(t))*(diff(q2(t),t)-diff(q1(t),t))-diff(q1(t),t)*diff(q2(t),t)*sin(q2(t)-q1(t))+19.62*sin(q1(t)) = ...

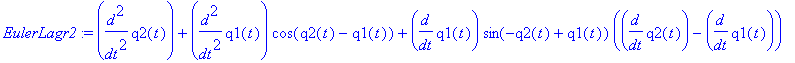
EulerLagr2 := diff(q2(t),`$`(t,2))+diff(q1(t),`$`(t,2))*cos(q2(t)-q1(t))+diff(q1(t),t)*sin(-q2(t)+q1(t))*(diff(q2(t),t)-diff(q1(t),t))+diff(q1(t),t)*diff(q2(t),t)*sin(q2(t)-q1(t))+9.81*sin(q2(t)) = -.2...
EulerLagr2 := diff(q2(t),`$`(t,2))+diff(q1(t),`$`(t,2))*cos(q2(t)-q1(t))+diff(q1(t),t)*sin(-q2(t)+q1(t))*(diff(q2(t),t)-diff(q1(t),t))+diff(q1(t),t)*diff(q2(t),t)*sin(q2(t)-q1(t))+9.81*sin(q2(t)) = -.2...

>    A_q1:=Pi:
A_v1:=-1:
A_q2:=Pi/2:
A_v2:=0:

A:=dsolve({EulerLagr1,EulerLagr2,q1(0)=A_q1,D(q1)(0)=A_v1,q2(0)=A_q2,D(q2)(0)=A_v2},[q1(t),q2(t)],type=numeric,output=listprocedure);

A := [t = proc (t) local res, data, solnproc; option `Copyright (c) 1993 by the University of Waterloo. All rights reserved.`; data := module () local Data; export Get, Set; end module; solnproc := dat...
A := [t = proc (t) local res, data, solnproc; option `Copyright (c) 1993 by the University of Waterloo. All rights reserved.`; data := module () local Data; export Get, Set; end module; solnproc := dat...

>    with(plots):
with(plottools): 

Warning, the previous binding of the name arrow has been removed and it now has an assigned value

>    tend:=30:                                       P1:=odeplot(A,[t,q1(t)],0..tend,color=black):
P2:=odeplot(A,[t,q2(t)],0..tend,color=blue):
display(P1,P2);

[Maple Plot]

>    q_1:= eval(q1(t),A):
q_2:= eval(q2(t),A):
y1:=t->-l1*cos(q_1(t)):
y2:=t->-l2*cos(q_2(t))-l1*cos(q_1(t)):
x1:=t->l1*sin(q_1(t)):
x2:=t->l2*sin(q_2(t))+l1*sin(q_1(t)):



plot({x1(t),x2(t)},t=0..3):

>    frames:=200;
for i from 0 by 1 to frames do

Masse1[i]:=display(disk([x1(i*tend/frames),y1(i*tend/frames)], 0.1, color=red)):
Masse2[i]:=display(disk([x2(i*tend/frames),y2(i*tend/frames)], 0.1, color=blue)):
Seil1[i]:=curve([[0,0],[x1(i*tend/frames),y1(i*tend/frames)]],color=black,thickness=2):
Seil2[i]:=curve([[x1(i*tend/frames),y1(i*tend/frames)],[x2(i*tend/frames),y2(i*tend/frames)]],color=black,thickness=2):

Ani[i] := display( {Masse1[i],Masse2[i],Seil1[i],Seil2[i]}, axes=normal);
od:

frames := 200

>    display([seq(Ani[i],i=0..frames)],insequence=true,scaling=constrained);

[Maple Plot]

>   

>   

>