Musterlösung zum Übungsblatt Nr. 8
Musterlösung zur Aufgabe 1 (10 Punkte)
Das folgende C++ Programm beinhaltet die Klasse 'class Integral' und die inline-Methode 'inline double Integral::f(double x){ ... }'. In der 'int main(){ ...}' Funktion werden vier Integral-Objekte mittels Konstruktor-Aufruf erzeugt, wobei diese Integral-Instanzen sich in der Anzahl der Teilintervalle $ts$ unterscheiden.
// Musterlösung der Aufgabe 1 des Übungsblattes Nr.8 /* Die Klasse Integral berechnet das bestimmte Integral * einer Funktion f(x) in den Grenzen [a,b] * mittels einer stückweise numerischen Integration (ts Teilintervalle) * und benutzt in jedem der Teilintervalle die N=4 Integrationsregel */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) //Definition der Klasse 'Integral' class Integral{ // Private Instanzvariablen (Daten-Member) der Klasse double a; // Untergrenze des bestimmten Integrals double b; // Obergrenze des bestimmten Integrals unsigned ts; // Anzahl der Teilintervalle (wurde zuvor mit der Variable ts bezeichnet) // Oeffentliche Konstruktoren und Member-Funktionen der Klasse public: // Konstruktor mit drei Argumenten und Standardinitialisierungen Integral(double set_a = 0, double set_b = 1, unsigned set_ts = 10) : a{set_a}, b{set_b}, ts{set_ts} {} // Member-Funktionen der Klasse double f(double x); // Deklaration der Member-Funktion f(x) (Definition findet ausserhalb der Klasse statt) double integrate() { // Member-Funktion der Klasse zur Berechnung des bestimmten Integrals double I_wert = 0; // Variable fuer den zu berechnenden Integralwert double h = (b-a)/(4*ts); // Deklaration des h-Wertes fuer die N=4 Integrationsregel double x_u; // x-Untergrenze der Teilintegration for(unsigned i = 0; i < ts; ++i){ // Schleifen Anfang ueber die einzelnen Teilintegrationen x_u = a + 4*i*h; // Setzen der neuen x-Untergrenze der nächsten Teilintegration I_wert += 2*h/45*(7*f(x_u) + 32*f(x_u+h) + 12*f(x_u+2*h) + 32*f(x_u+3*h) + 7*f(x_u+4*h)); // N=4 Regel } // Ende for-Schleife return I_wert; // Rueckgabe des berechnenden Integralwertes } // Ende der Member-Funktion integrate() }; inline double Integral::f(double x){ // Definition der Funktion f(x) als inline-Methode der Klasse Integral double wert; wert = 10 * exp(-x/5) * sin(3*x); // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } int main(){ // Hauptfunktion double I_analyt = - 4.7587485166819485; // Analytischer Wert des Integrals, mittels Jupyter-Sympy berechnet (Grenzen [a,b]=[1,2]) Integral I1 {1,2}; // Benutzt Integral(a,b) mit ts=10 (Standardwert) Integral I2 {1,2,50}; // Benutzt Integral(a,b,ts) mit ts=50 Integral I3 {1,2,100}; // Benutzt Integral(a,b,ts) mit ts=100 Integral I4 {1,2,1000000}; // Benutzt Integral(a,b,ts) mit ts=1000000 double result_I1 = I1.integrate(); // Berechne den Wert des Integrals mit ts=10 double result_I2 = I2.integrate(); // Berechne den Wert des Integrals mit ts=50 double result_I3 = I3.integrate(); // Berechne den Wert des Integrals mit ts=100 double result_I4 = I4.integrate(); // Berechne den Wert des Integrals mit ts=1000000 // Terminalausgabe printf("I1 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 10) \n", result_I1, result_I1 - I_analyt); printf("I2 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 50) \n", result_I2, result_I2 - I_analyt); printf("I3 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 100) \n", result_I3, result_I3 - I_analyt); printf("I4 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 1 Million) \n", result_I4, result_I4 - I_analyt); printf("Analytisch I = %20.14f\n", I_analyt); }
Führt man das Programm A8_1.cpp aus, so erhält man die folgende Terminalausgabe (siehe erste, obere Ausgabe):
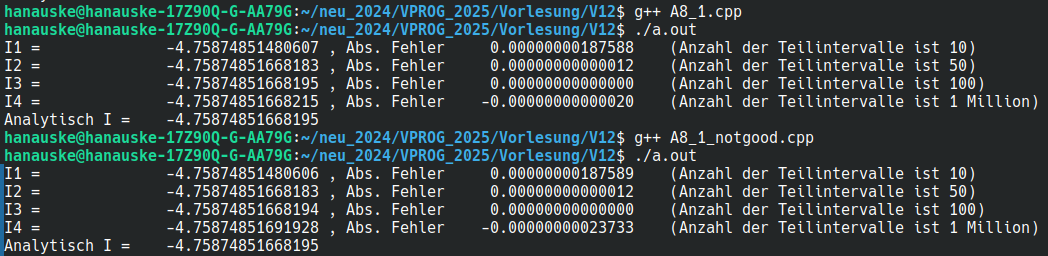
Man erkennt, dass der absolute Fehler in der approximativen Berechnung des Integralwertes , zunächst, mit steigender Anzahl der Teilintervalle (steigendem Wert von $ts$) kleiner wird. Bei $ts=100$ ist der berechnete Wert auf 14 Nachkommastellen genau! Erhöht man die Anzahl der Teilintervalle jedoch immer weiter, so steigt der Fehler, bei der Berechnung mit sehr hohen Werten von $ts$, jedoch wieder an. Bei $ts=1000000$ ist der berechnete Wert nur noch auf 12 Nachkommastellen genau! Der Grund hierfür liegt in einer kumulativen Erzeugung von Rundungsfehlern innerhalb der for-Schleife der Klasse. Der Programmierer ist somit in der Exaktheit seiner numerischen Berechnungen beschränkt. Das Gewicht solcher Rundungsfehler kann sich bei einer unvorteilhaften Inkrementierung von Gleitkommazahlen erhöhen.
In dem unteren C++ Programm wurde z.B. die Art und Weise, wie sich die Teiluntergrenze $x_u$ innerhalb der for-Schleife erhöht verändert. Führt man das Programm A8_1_notgood.cpp aus, so erhält man die oben dargestellt Terminalausgabe (siehe zweite, untere Ausgabe). Bei $ts=1000000$ ist der berechnete Wert nur noch auf 9 Nachkommastellen genau, da durch die Anweisung 'x_u = x_u + 4*h;' in jedem neuen Teilintervall der Rundungsfehler, von den zuvor berechneten, mit aufaddiert wird.
// Musterlösung der Aufgabe 1 des Übungsblattes Nr.8 /* Die Klasse Integral berechnet das bestimmte Integral * einer Funktion f(x) in den Grenzen [a,b] * mittels einer stückweise numerischen Integration (ts Teilintervalle) * und benutzt in jedem der Teilintervalle die N=4 Integrationsregel * * In dieser Version wurde eine unvorteilhafte Implementierung der Erhoehung von x_u benutzt */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) //Definition der Klasse 'Integral' class Integral{ // Private Instanzvariablen (Daten-Member) der Klasse double a; // Untergrenze des bestimmten Integrals double b; // Obergrenze des bestimmten Integrals unsigned ts; // Anzahl der Teilintervalle (wurde zuvor mit der Variable ts bezeichnet) // Oeffentliche Konstruktoren und Member-Funktionen der Klasse public: // Konstruktor mit drei Argumenten und Standardinitialisierungen Integral(double set_a = 0, double set_b = 1, unsigned set_ts = 10) : a{set_a}, b{set_b}, ts{set_ts} {} // Member-Funktionen der Klasse double f(double x); // Deklaration der Member-Funktion f(x) (Definition findet ausserhalb der Klasse statt) double integrate() { // Member-Funktion der Klasse zur Berechnung des bestimmten Integrals double I_wert = 0; // Variable fuer den zu berechnenden Integralwert double h = (b-a)/(4*ts); // Deklaration des h-Wertes fuer die N=4 Integrationsregel double x_u = a - 4*h; // x-Untergrenze der Teilintegration for(unsigned i = 0; i < ts; ++i){ // Schleifen Anfang ueber die einzelnen Teilintegrationen x_u = x_u + 4*h; // Setzen der neuen x-Untergrenze der nächsten Teilintegration: nicht gut!, besser : // x_u = a + 4*i*h; // Setzen der neuen x-Untergrenze der nächsten Teilintegration I_wert += 2*h/45*(7*f(x_u) + 32*f(x_u+h) + 12*f(x_u+2*h) + 32*f(x_u+3*h) + 7*f(x_u+4*h)); // N=4 Regel } // Ende for-Schleife return I_wert; // Rueckgabe des berechnenden Integralwertes } // Ende der Member-Funktion integrate() }; inline double Integral::f(double x){ // Definition der Funktion f(x) als inline-Methode der Klasse Integral double wert; wert = 10 * exp(-x/5) * sin(3*x); // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } int main(){ // Hauptfunktion double I_analyt = - 4.7587485166819485; // Analytischer Wert des Integrals, mittels Jupyter-Sympy berechnet (Grenzen [a,b]=[1,2]) Integral I1 {1,2}; // Benutzt Integral(a,b) mit ts=10 (Standardwert) Integral I2 {1,2,50}; // Benutzt Integral(a,b,ts) mit ts=50 Integral I3 {1,2,100}; // Benutzt Integral(a,b,ts) mit ts=100 Integral I4 {1,2,1000000}; // Benutzt Integral(a,b,ts) mit ts=1000000 double result_I1 = I1.integrate(); // Berechne den Wert des Integrals mit ts=10 double result_I2 = I2.integrate(); // Berechne den Wert des Integrals mit ts=50 double result_I3 = I3.integrate(); // Berechne den Wert des Integrals mit ts=100 double result_I4 = I4.integrate(); // Berechne den Wert des Integrals mit ts=1000000 // Terminalausgabe printf("I1 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 10) \n", result_I1, result_I1 - I_analyt); printf("I2 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 50) \n", result_I2, result_I2 - I_analyt); printf("I3 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 100) \n", result_I3, result_I3 - I_analyt); printf("I4 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 1 Million) \n", result_I4, result_I4 - I_analyt); printf("Analytisch I = %20.14f\n", I_analyt); }
Den Algorithmus der Integration hätte man wohl besser in einer normalen C++ Funktion implementiert, da das Deklarieren der Integral-Instanzen und die erst danach folgende Integralberechnung ein wenig umständlich ist.
Musterlösung zur Aufgabe 2 (10 Punkte)
Das folgende C++ Programm zeigt die Umformulierung des C++-Programms Mandelbrot.cpp mittels einer C++-Klasse.
/* Musterlösung der Aufgabe 2 des Übungsblattes Nr.8 * Erstellung einer Klasse zur Berechnung der Mandelbrot-Menge * Ausgabe zum Plotten mit Python mittels: "./a.out > Mandelbrot_class.dat" */ #include <iostream> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <vector> // Sequenzieller Container vector<Type> der Standardbibliothek #include <complex> // Standardbibliothek fuer komplexwertige Zahlen using namespace std; // Benutze den Namensraum std class Mandelbrot { // Private Instanzvariablen const double x_min; // Realteil Minimum const double x_max; // Realteil Maximum const double y_min; // Imaginärteil Minimum const double y_max; // Imaginärteil Maximum const int iter_max; // Maximale Anzahl an Iterationen const int N; // Anzahl der Punkte pro Intervall vector<vector<int>> output; // Deklaration eine int Vektor-Matrix zum speichern der Loesungen // Private Member-Funktion (berechnet die Anzahl der Iterationen bis |z|>2 für einen komplexwertigen Punkt c) // Falls immer |z|<=2, dann iter=iter_max int computeIterations(complex<double> c) { complex<double> z(0, 0); // Definition des Anfangswertes der komplexwertigen Folge int iter = 0; // Iterationen, die benoetigt werden bis |z|>2 while (abs(z) <= 2.0 && iter < iter_max) { // while-Schleife ueber die einzelnen Folgenwerte z = z * z + c; // Bildungsgesetz der komplexwertigen Folge iter++; // Benoetigte Iteration + 1 } // Ende while-Schleife return iter; // Rückgabe der Anzahl der Iterationen } // Ende Private Member-Funktion public: // Öffentlicher Konstruktor mit Standardargumenten zur Initialisierung der Instanzvariablen Mandelbrot(double set_x_min = -1.9, double set_x_max = 0.5, double set_y_min = -1.2, double set_y_max = 1.2, int set_iter_max = 100, int set_N = 1000) : x_min(set_x_min), x_max(set_x_max), y_min(set_y_min), y_max(set_y_max), iter_max(set_iter_max), N(set_N) { // Dimensionen der output-Matrix werden festgelegt um Index-Zugriff zu ermöglichen, Null-Matrix output.resize(N, std::vector<int>(N, 0)); } // Öffentliche Member-Funktion (berechnet die Mandelbrot-Menge) void calculate() { const double h_x = (x_max - x_min) / N; // Abstand zwischen den aequidistanten Punkten des x-Intervalls const double h_y = (y_max - y_min) / N; // Abstand zwischen den aequidistanten Punkten des y-Intervalls for (int k = 0; k < N; ++k) { // for-Schleife ueber die Punkte des x-Intervalls for (int l = 0; l < N; ++l) { // for-Schleife ueber die Punkte des y-Intervalls complex<double> c(x_min + k * h_x, y_min + l * h_y); // Definition der komplexen Zahl c = x +i*y output[k][l] = computeIterations(c); // Berechnung der Anzahl der Iterationen für einen Punkt c } // Ende for-Schleife y-Intervalls } // Ende for-Schleife x-Intervalls } // Ende der Methode calculate() // Öffentliche Member-Funktion (Ausgabe der Loesungswerte mittels einer bereichsbasierten for-Schleife) void printOutput() const { for (const auto& output_k : output) { for (const int wert : output_k) { cout << wert << " "; } cout << endl; } } }; int main() { // Mandelbrot mandelbrot; // Instanz der Klasse mit Standardwerten (Apfelmännchen) // Mandelbrot mandelbrot(-0.8, -0.775, 0.13, 0.155, 500, 2000); // Verwendung des Konstruktors (Bereich im Tal der Seepferdchen) Mandelbrot mandelbrot(-0.74675, -0.74575, 0.098, 0.0991, 1000, 2000); // Verwendung des Konstruktors (Seepferdchenschwanz) mandelbrot.calculate(); // Mandelbrot-Menge berechnen mandelbrot.printOutput(); // Ergebnisse ausgeben }
Innerhalb der Klasse 'Mandelbrot' werden zunächst die privaten Instanzvariablen der Klasse deklariert, wobei die Initialisierung dieser Variablen später im Konstruktor vollzogen wird. Die Integer-Vektor-Matrix 'vector<vector<int>> output; ', die zum Speichern der gesamten Iterationswerte, ab welchen Werten eine Divergenz der Folge auftritt, benutzt wird, ist ebenfalls im privaten Bereich der Klasse deklariert. Der Übersichtlichkeit halber ist dort auch eine private Member-Funktion 'int computeIterations(complex<double> c)' definiert, die diese Anzahl der Iterationen für einen komplexwertigen Punkt $c \in ℂ$ berechnet.
Im öffentlichen Bereich der Klasse wird zunächst der Konstruktor definiert. Innerhalb der Argumentenliste des Konstruktors werden die privaten Instanzvariablen der Klasse initialisiert, sodass der Benutzer in einfacher Weise den gewünschten Zahlenraum der komplexen Zahlen $c = x +i \cdot y \in ℂ$ der Mandelbrot-Menge auswählen kann. Diese Initialisierung erfolgt hierbei speziell mit den Werten, die den gesamten Bereich der Mandelbrot-Menge darstellen (Re(c)$=x \in [-1.9,0.5]$ und Im(c)$=y \in [-1.2,1.2]$) und bilden somit das Mandelbrot-Apfelmännchen ab. Wird vom Hauptprogramm aus, mittels des Standard-Konstruktors (Mandelbrot mandelbrot) eine Instanz der Klasse erzeugt, dann werden diese Werte automatisch initialisiert. Im Anweisungsblock des Konstruktors wird zusätzlich noch die Dimension der output-Matrix festgelegt und die Matrix mit Nullen initialisiert. Dies ist effizienter und ermöglicht einen späteren Index-Zugriff auf die einzelnen Elemente. Im öffentlichen Bereich der Klasse wird danach die Member-Funktion 'void calculate()' definiert, die die Mandelbrot-Menge berechnet, indem sie den Raum der komplexen Zahlen $c = x +i \cdot y \in ℂ$ in $N \cdot N = 1000 \cdot 1000$ Gitterpunkte untergliedert und für jeden dieser Punkte prüft, ob die Folge divergiert. Am Ende der Klasse wird dann noch die öffentliche Member-Funktion 'void printOutput() const' definiert, die die berechneten Werte mittels einer bereichsbasierten for-Schleife im Terminal ausgibt.
In der Hauptfunktion des Programms wurden zunächst die im Unterpunkt C++ Container und die vector Klasse der Standardbibliothek dargestellten Ergebnissen überprüft (siehe die ersten beiden auskommentierten Zeilen in der Hauptfunktion). Mittels des Konstruktors 'Mandelbrot mandelbrot(-0.74675, -0.74575, 0.098, 0.0991, 1000, 2000);' wurde dann in den vorgegebenen Bereich der Mandelbrot-Menge (Re(c)$=x \in [-0.74675, -0.74575]$ und Im(c)$=y \in [0.098, 0.0991]$) fokussiert und eine hohe Auflösung benutzt ( int set_iter_max = 1000, int set_N = 2000). Diese Mandelbrot-Menge wurde dann berechnet (mandelbrot.calculate(); ) und ausgegeben (mandelbrot.printOutput(); ).
Die berechneten Daten wurden in die Datei 'Mandelbrot_class.dat' umgeleitet und mittels des folgenden Python-Skripts geplottet, wobei eine andere Farbwahl (plt.cm.copper) gewählt wurde.
# Python Programm zum Plotten der berechneten Daten von (Mandelbrot_class.cpp) import matplotlib.pyplot as plt # Python Bibliothek zum Plotten (siehe https://matplotlib.org/ ) import matplotlib import numpy as np # Python Bibliothek fuer Mathematisches (siehe https://numpy.org/ ) # Festlegung einiger Bildparameter params = { 'figure.figsize' : [12,8], 'axes.titlesize' : 14, 'axes.labelsize' : 16, 'xtick.labelsize' : 14 , 'ytick.labelsize' : 14 } matplotlib.rcParams.update(params) data = np.genfromtxt("./Mandelbrot_class.dat") # Einlesen der berechneten Daten von Mandelbrot_class.cpp # Bereich der komplexen Zahlen der Mandelbrotmenge x_min, x_max, y_min, y_max = -0.74675, -0.74575, 0.098, 0.0991 plt.imshow(data, extent=[y_min, y_max, x_max, x_min], cmap=plt.cm.copper) # Plotten der Daten # Farbskala, Titel und Labels plt.colorbar(label='Iterationen') plt.title('Mandelbrotmenge (Seepferdchenschwanz)') plt.ylabel('x=Re(c)') plt.xlabel('y=Im(c)') # Speichern der Abbildung als Bild plt.savefig("Mandelbrot_class.png", dpi=200,bbox_inches="tight",pad_inches=0.05,format="png") plt.show() # Zusaetzliches Darstellen der Abbildung in einem separaten Fenster
Die folgenden Abbildungen wurde mittels der Programme Mandelbrot_class.cpp und Mandelbrot_class.py angefertigt.
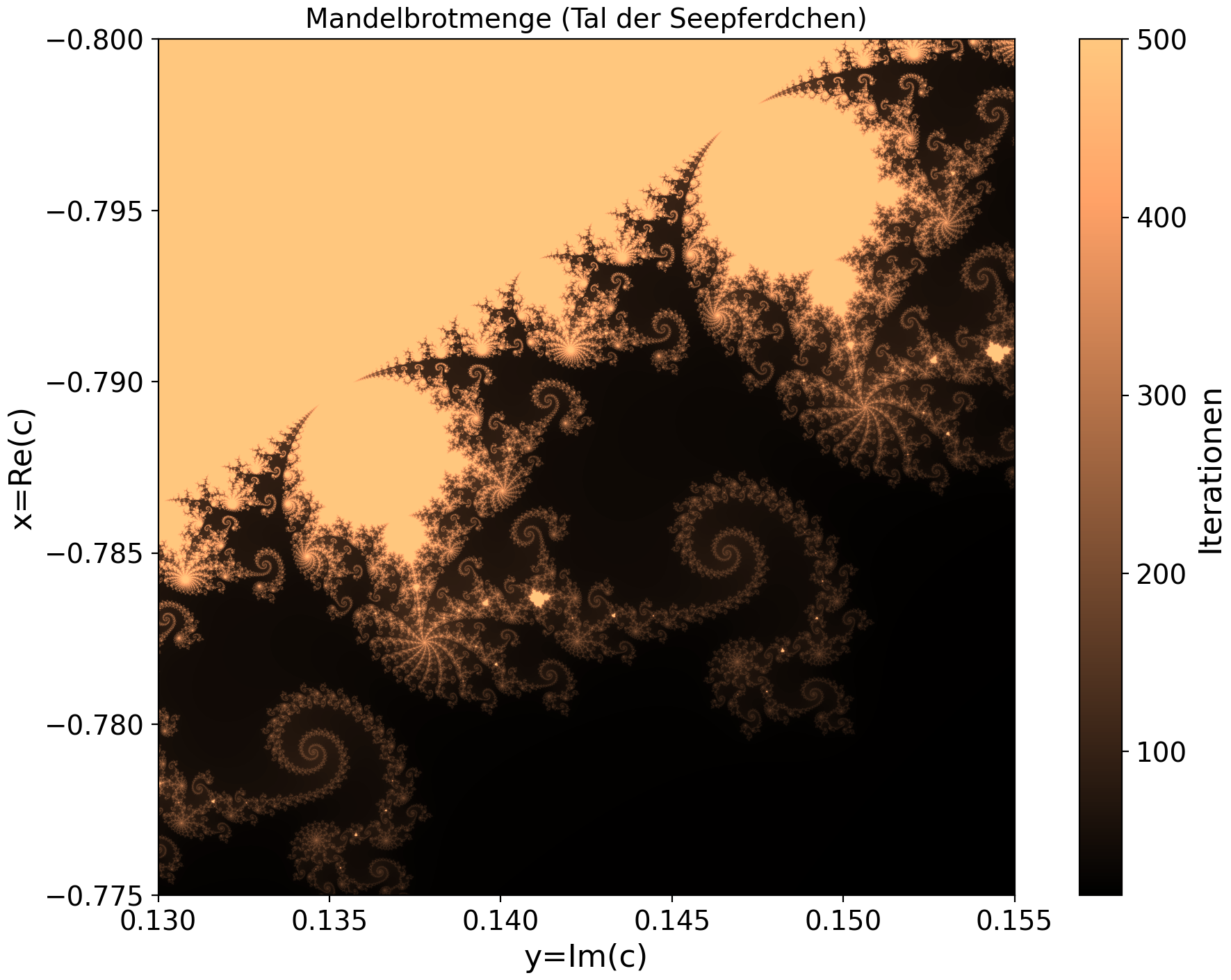
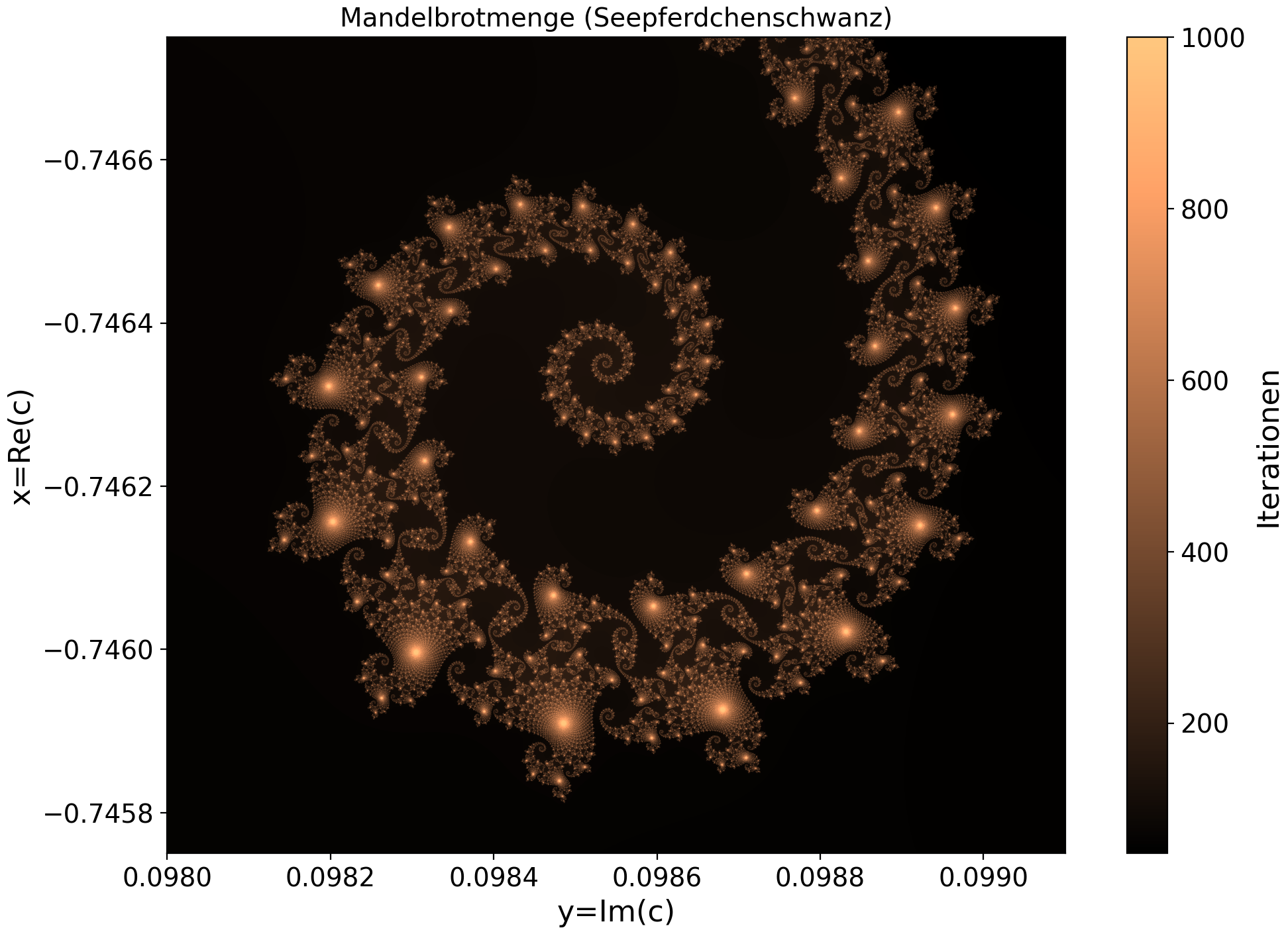
Die linke untere Abbildung zeigt den Bereich des 'Seepferdchentals', welches bereits im Unterpunkt C++ Container und die vector Klasse der Standardbibliothek in einer anderen Colormap dargestellt wurde. Die rechte untere Abbildung fokussiert in den vorgegebenen Bereich (Re(c)$=x \in [-0.74675, -0.74575]$ und Im(c)$=y \in [0.098, 0.0991]$) und zeigt die filigrane Struktur eines 'Seepferdchenschwanzes'.