Musterlösung zum Übungsblatt Nr. 5
Musterlösung zur Aufgabe 1 (7.5 Punkte)
Das folgende C++ Programm basiert auf dem Programm Lagrange_Polynom_1.cpp. Der Kern-Algorithmus des Programms wurde jedoch in eine Funktion "void Lagrange_Poly( ... )" ausgelagert.
// Musterlösung der Aufgabe 1 des Übungsblattes Nr.5 /* Die Berechnung des Lagrange Polynoms wurde in die * Funktion Lagrange_Poly( ... ) ausgelagert */ #include <iostream> // Ein- und Ausgabebibliothek double f(double x){ // Deklaration und Definition der Funktion f(x) die approximiert werden soll double wert; wert = 1.0/x; // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } // Ende der Funktion f(x) void Lagrange_Poly(double* points, unsigned int N_points, double a, double b, unsigned int N_xp, double* xp, double* fp, double* Pfp){ double dx = (b - a)/N_xp; // Abstand dx zwischen den aequidistanten Punkten des x-Intervalls double x; // Aktueller x-Wert double Lk; // Deklaration einer Variable, die fuer Zwischenrechnungen benoetigt wird for(unsigned int j = 0; j <= N_xp; ++j){ // For-Schleife die ueber die einzelnen Punkte des x-Intervalls geht x = a + j*dx; // Aktueller x-Wert xp[j]=x; // Eintrag des aktuellen x-Wertes in das x-Array fp[j]=f(x); // Eintrag des aktuellen f(x)-Wertes in das f(x)-Array Pfp[j]=0; // Initialisierung des j-ten Polynom-Arrays mit 0 (Wert beim Anfang der Summenbildung) for(unsigned int k = 0; k < N_points; ++k){ // For-Schleife der Summation in der Lagrange Polynom Methode Lk=1; // Initialisierung der Produktvariable Lk mit 1 for(unsigned int i = 0; i < N_points; ++i){ // For-Schleife der Produktbildung in der Lagrange Polynom Methode if(i != k){ // Die Produktbildung soll nur fuer (i ungleich k) erfolgen Lk = Lk * (x - points[i])/(points[k] - points[i]); // Berechnung der Lk-Werte in der Lagrange Polynom Methode } // Ende if-Bedingung } // Ende for-Schleife der Produktbildung Pfp[j] = Pfp[j] + f(points[k])*Lk; // Kern-Gleichung in der Lagrange Polynom Methode } // Ende for-Schleife der Summenbildung } // Ende der for-Schleife ueber die einzelnen Punkte des x-Intervalls } // Ende der Funktion f(x) int main(){ // Hauptfunktion double points[] = { 2, 2.5, 4 }; // Deklaration und Initialisierung der Stützstellen als double-Array constexpr unsigned int N_points = sizeof(points)/sizeof(points[0]);// Anzahl der Punkte die zur Approximation verwendet werden double a=0.5; // Untergrenze des x-Intervalls in dem die Ergebnisse ausgegeben werden sollen double b=6; // Obergrenze des x-Intervalls in dem die Ergebnisse ausgegeben werden sollen constexpr unsigned int N_xp=300; // Anzahl der Punkte in die das x-Intervall aufgeteilt wird double xp[N_xp+1]; // Deklaration der x-Ausgabe-Punkte als double-Array double fp[N_xp+1]; // Deklaration der f(x)-Ausgabe-Punkte als double-Array double Pfp[N_xp+1]; // Deklaration der Ausgabe-Punkte des approximierten Polynoms als double-Array printf("# x-Werte der %3d Stuetzstellen-Punkte: \n", N_points); // Beschreibung der ausgegebenen Groessen for(unsigned int k = 0; k < N_points; ++k){ // For-Schleife der Ausgabe der Stuetzstellen x-Werte printf("%10.5f",points[k]); // Ausgabe der Stuetzpunkte } // Ende for-Schleife der Ausgabe printf("\n"); // Zeilenumbruch printf("# 0: Index j \n# 1: x-Wert \n# 2: f(x)-Wert \n"); // Beschreibung der ausgegebenen Groessen printf("# 3: Approximierter Wert des Lagrange Polynoms P(x) \n"); // Beschreibung der ausgegebenen Groessen printf("# 4: Fehler zum wirklichen Wert f(x)-P(x) \n"); // Beschreibung der ausgegebenen Groessen Lagrange_Poly(points,N_points,a,b,N_xp,xp,fp,Pfp); // Berechnung der Wertetabelle des Lagrange Polynoms for(unsigned int j = 0; j <= N_xp; ++j){ // For-Schleife der separaten Ausgabe der berechneten Werte printf("%3d %14.10f %14.10f %14.10f %14.10f \n",j, xp[j], fp[j], Pfp[j], (fp[j] - Pfp[j])); // Ausgabe der berechneten Werte } // Ende for-Schleife der Ausgabe } // Ende der Hauptfunktion
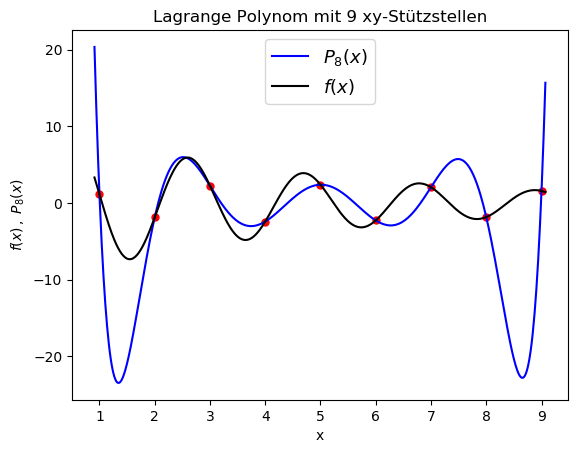
Die ersten fünf Einträge in der Argumentenliste der Funktion werden bei ihrem Aufruf initialisiert und die darauf folgenden drei Argumente stellen die Zeiger auf die im Hauptprogramm deklarierten Arrays double xp[N_xp+1], double fp[N_xp+1] und double Pfp[N_xp+1] dar. Es wurde das Programm mit den Vorgaben ($f(x)=1/x$ und $\vec{x}=\left( 2, 2.5, 4 \right)$) getestet und das im Terminal ausgegebene Ergebnis entsprach exakt den zuvor berechneten Werten. Nun wurde das Lagrange Polynom vom Grade $n=8$ im Teilintervall $[a,b]=[0.91,9.07]$ mit $f(x) = 10 \, e^{-x/5} \cdot \hbox{sin}(3 \, x)$ und $\vec{x}=\left( 1,2,3,4,5,6,7,8,9 \right)$ berechnet (siehe A5_1a.cpp). Die nebenstehende Abbildung visualisiert die Ergebnisse des Programms (das zugehörige Python Skript findet man unter PythonPlot_A5_1.py).
Musterlösung zur Aufgabe 2 (7.5 Punkte)
Der unten abgebildete C++ Quelltext stellt die Musterlösung zur Aufgabe 2 dar. Die ersten 40 Zahlenwerte der Fibonacci-Folge wurden in einem eindimensionalen C++ Array gespeichert, das am Anfang des Programms zunächst deklariert wurde 'unsigned int f[N];'. Danach wurden die ersten beiden Folgenglieder mit '1' initialisiert. Die eigentliche Implementierung des rekursiv definierten Bildungsgesetzes der Fibonacci-Folge wurde dann mittels der Indexschreibweise innerhalb der for-Schleife realisiert:
$f_n = f_{n-1} + f_{n-2} \, \Rightarrow \quad$ f[n] = f[n-1] + f[n-2];
Das Verhältnis zweier aufeinanderfolgender Zahlen der Fibonacci-Folge ($\frac{f_n}{f_{n-1}}$), welches im Grenzwert $\lim \limits_{n \to \infty}$ gegen die irrationale Zahl des Goldenen Schnitts $\Phi \approx 1.618033988749894848204586834$ konvergiert, wurde mittels des folgenden Ausdrucks im Terminal ausgegeben: (double)(f[n])/f[n-1]
Man erkennt hierbei deutlich, das die mathematische Formulierung und die C++ Array-Indexschreibweise deutliche Ähnlichkeiten besitzt.
/* Musterlösung der Aufgabe 2 des Übungsblattes Nr.5 * Fibonacci-Folge mittels eines eindimensionalen Arrays * und Vergleich mit der irrationalen Zahl des Goldenen Schnitts */ #include <iostream> // Ein- und Ausgabebibliothek int main(){ // Hauptfunktion constexpr unsigned int N = 40; // Deklaration und Initialisierung des maximalen Folgengliedes unsigned long f[N]; // Deklaration der Fibonacci-Zahlen als ein eindimensionales Array f[0] = 1; // Initialisierung des 0.ten Folgengliedes f[1] = 1; // Initialisierung des 1.ten Folgengliedes printf("# 0: Folgenindex n \n# 1: Fibonacci Zahl \n# 2: Goldener Schnitt \n"); // Beschreibung der ausgegebenen Groessen printf("%4i %12li \n",0,f[0]); // Ausgabe des 0. Folgengliedes printf("%4i %12li \n",1,f[1]); // Ausgabe des 1. Folgengliedes for(unsigned int n=2; n<N; ++n){ // Schleifen Anfang f[n] = f[n-1] + f[n-2]; // Rekursives Bildungsgesetz der Fibonacci-Folge printf("%4i %12li %20.17Lf \n",n, f[n], (long double)(f[n])/f[n-1]); // Ausgabe der berechneten Groessen } // Ende der Schleife printf("# Approximierte irrationale Zahl des Goldenen Schnitts: %20.17Lf \n", (long double)(f[N-1])/f[N-2]); printf("# Wirklicher Zahlenwert des Goldenen Schnitts : %20.17Lf \n", 1.618033988749894848204586834L); }
Musterlösung zur Aufgabe 3 (6 Punkte)
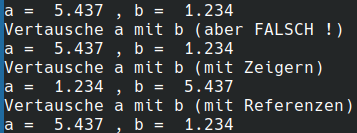
Im unten dargestellten C++ Programm wurden drei Tausch-Funktionen definiert, wobei nur zwei von diesen eine wirkliche Vertauschung der Zahlenwerte von a und b realisieren. Die Terminalausgabe des Programms ist in der Abbildung rechts zu sehen. Die Funktion "void Tausche_ab_FALSCH(double a, double b){ ... }" ist ein FALSCHER Versuch einer Tauschfunktion! Die Funktion benutzt in der Argumentenliste direkt die double-Variablen double a und double b (Methode Call-by-Value). Der Gültigkeitsbereich dieser lokalen Variablen ist jedoch lediglich auf den 'Block von Anweisungen' der Funktion beschränkt und kann deshalb die Werte der Variablen a und b der main()-Funktion nicht verändern bzw. austauschen. Die Funktion "void Tausche_ab_p(double* pa, double* pb){ ... }" benutzt hingegen die Zeiger auf a und auf b in der Argumentenliste und kann somit die Werte vertauschen (Methode Call-by-Pointer). Im Programm wurde zunächst die ursprünglichen initialisierten Werte der Variablen a und b ausgegeben, danach die falsche Tauschfunktion aufgerufen und erneut die aktuellen Werte von a und b im Terminal ausgegeben. Dann wurde die "richtige" Tauschfunktion (Tausche_ab_p) ausgeführt und erneut der Wert der Variablen ausgegeben. In der dritten Tausch-Funktion verwenden wir schließlich die Methode Call-by-Reference und vertauschen dadurch die Werte wieder zurück zu ihren ursprunglich initialisierten Werten.
// Musterlösung der Aufgabe 3 des Übungsblattes Nr.5 #include <iostream> // Ein- und Ausgabebibliothek // Tauschfunktion mit Argumentenliste von Zeigern auf a und b void Tausche_ab_p(double* pa, double* pb){ printf("Vertausche a mit b (mit Zeigern)\n"); double tmp = *(pa); // Speichert den Wert von a *(pa) = *(pb); // Schreibt den Wert von b in a *(pb) = tmp; // Schreibt den alten Wert von a in b } // Tauschfunktion mit Argumentenliste von Referenzen auf a und b void Tausche_ab_r(double& ra, double& rb){ printf("Vertausche a mit b (mit Referenzen)\n"); double tmp = ra; // Speichert den Wert von a ra = rb; // Schreibt den Wert von b in a rb = tmp; // Schreibt den alten Wert von a in b } // Tauschfunktion mit Argumentenliste von double Variablen a und b // Problem: a und b sind lokale Variablen, die ihren Gueltigkeitsbereich // nur innerhalb des Anweisungsblockes der Funktion hat void Tausche_ab_FALSCH(double a, double b){ printf("Vertausche a mit b (aber FALSCH !) \n"); double tmp = a; // Speichert den Wert von a a = b; // Schreibt den Wert von b in a b = tmp; // Schreibt den alten Wert von a in b } int main(){ // Hauptfunktion double a = 5.437; // Definition a double b = 1.234; // Definition b printf("a = %6.3f , b = %6.3f \n", a,b); Tausche_ab_FALSCH(a,b); // führe falsche Tauschfunktion aus printf("a = %6.3f , b = %6.3f \n", a,b); Tausche_ab_p(&a,&b); // führe richtige Tauschfunktion aus (mit Zeigern) printf("a = %6.3f , b = %6.3f \n", a,b); Tausche_ab_r(a,b); // führe richtige Tauschfunktion aus (mit Referenzen) printf("a = %6.3f , b = %6.3f \n", a,b); }