Musterlösung zum Übungsblatt Nr. 4
Musterlösung zur Aufgabe 1 (7.5 Punkte)
Die Berechnung des Schnittpunktes der Funktion $g(x)=x^3$ mit der Funktion $h(x)=$ln$(x)+5$ ist gleichbedeutend mit der Nullstellensuche der Funktion $f(x) := h(x) - g(x) = $ ln$(x) + 5 - x^3$. Das folgende C++ Programm stellt eine Musterlösung zur Aufgabe 1 dar:
// Musterlösung der Aufgabe 1 des Übungsblattes Nr.4 /* Methode der Bisektion (Intervallhalbierungsverfahren) * Berechnung des Schnittpunktes der Funktionen g(x)=x^3 und h(x)=ln(x)+5 im Intervall [0.25,2.5] * entspricht einer Nullstellensuche der Funktion f(x)=ln(x)+5-x^3 * Ausgabe zum Plotten (Gnuplot oder Python) mittels: "./a.out > A4_1.dat" */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) double f (double x) { // Deklaration und Definition der Funktion f(x) double wert; // Lokale double-Variable (nur im Bereich der Funktion gültig) wert = log(x) + 5 - pow(x,3); // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } // Ende der Funktion f(x) int main(){ // Hauptfunktion int i; // Deklaration des Laufindex als ganze Zahl double a = 0.25; // Untergrenze des Intervalls [a,b] in dem f(x)=0 gelten soll double b = 2.5; // Obergrenze des Intervalls [a,b] in dem f(x)=0 gelten soll const int N = 10; // Anzahl der Iterationen im Intervallhalbierungsverfahren double p, fp; // Deklaration der Variablen des approximierten x- und f(x)-Wertes der Nullstelle double fa=f(a); // Deklaration und Initialisierung des Funktionswertes f(a) an der Untergrenze const double Loes = 1.7729093296693715; // Wirklicher Wert des Schnittpunktes printf("# 0: Index i der Iteration \n# 1: Approximierter Wert der Nullstelle p_i \n"); // Beschreibung der ausgegebenen Groessen printf("# 2: Funktionswert f(p_i) \n# 3: Relativer Fehler zum wirklichen Wert |(p-p_i)/p| \n"); // Beschreibung der ausgegebenen Groessen printf("# 4: Untergrenze a \n# 5: Obergrenze b \n"); // Beschreibung der ausgegebenen Groessen for(i=0; i<=N; ++i){ // Schleifen Anfang p = a + (b-a)/2; // Festlegung des x-Wertes in der Mitte des Intervalls [a,b] (x=p) fp = f(p); // Berechnung des f(p)-Wertes in der Mitte des Intervalls [a,b] printf("%3d %14.10f %14.10f %14.10f %14.10f %14.10f \n",i, p, fp, fabs((Loes-p)/Loes), a, b); // Ausgabe der berechneten Werte if( fa*fp > 0 ){ // Falls der berechnete Wert f(p) das gleiche Vorzeichen hat wie f(a), dann ... a = p; // ... setze die Untergrenze auf a=p und ... fa = fp; // ... lege den neuen Funktionswert an der Untergrenze fest: f(a)=f(p) } else if( fa*fp < 0 ){ // Falls der berechnete Wert f(p) ein unterschiedliches Vorzeichen hat wie f(a), dann ... b = p; // ... setze die Obergrenze auf b=p } else{ // Falls durch der berechnete Funktionswert gerade Null ist (f(p)=0 -> f(a)*f(p)=0), dann ... i = N; // ... beende das Bisektion-Verfahren vorzeitig } // else Ende } // Ende der for-Schleife des Bisektion-Verfahres }
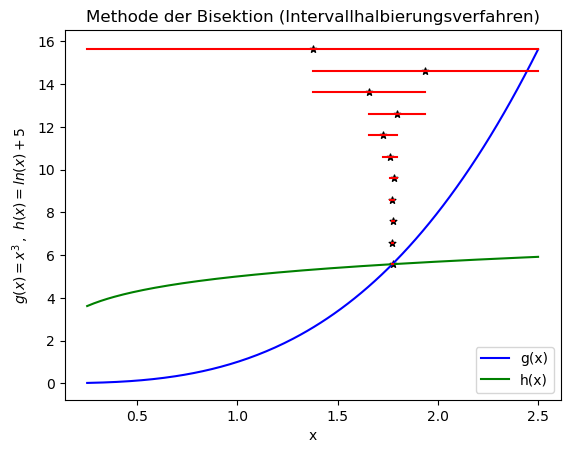
Das initiale Intervall $[0.25,2.5]$ wird mittels der Methode der Bisektion in jedem Iterationsschritt halbiert und die untere rechte Abbildung zeigt die Terminalausgabe des ausgeführten Programms.
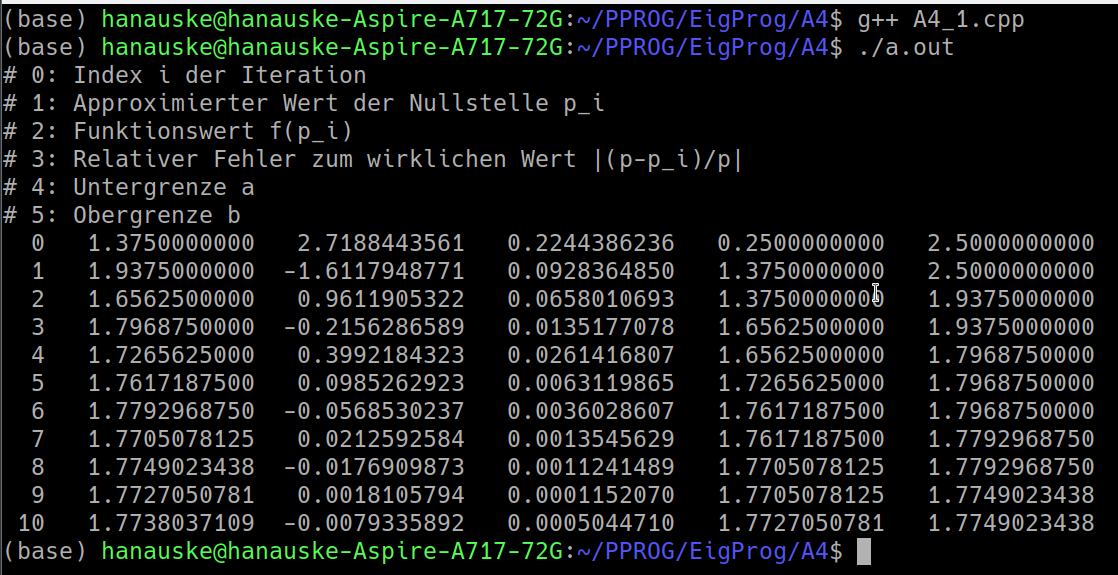
Man erkennt schon hier, dass der approximierte Wert der Nullstelle der Funktion $f(x)$ nach 10 Iterationen gut mit dem Literaturwert des x-Wertes des Schnittpunktes ($x = 1.7729093296693715...$) übereinstimmt. Die nebenstehende linke Abbildung verdeutlicht den Algorithmus der Intervallhalbierung in unserem Beispiel. Die Abbildung wurde mittels des unten angegebenen Python-Skriptes erstellt, wobei zunächst die Terminalausgabe des C++ Programms in eine Datei umgeleitet wurde (' ./a.out > A4_1.dat ').
# Python Programm zum Plotten der berechneten Daten von (A4_1.cpp) import matplotlib.pyplot as plt # Python Bibliothek zum Plotten (siehe https://matplotlib.org/ ) import numpy as np # Python Bibliothek fuer Mathematisches (siehe https://numpy.org/ ) data = np.genfromtxt("./A4_1.dat") # Einlesen der berechneten Daten von A4_1.cpp plt.title(r'Methode der Bisektion (Intervallhalbierungsverfahren)') # Titel der Abbildung plt.ylabel(r'$g(x)=x^3 \, , \,\, h(x)=ln(x)+5$') # Beschriftung y-Achse plt.xlabel('x') # Beschriftung x-Achse x_interval=np.linspace(data[0,4], data[0,5], 200) # x-Intervall [a,b] als Liste von 200 Zahlen plt.plot(x_interval,x_interval**3, color="blue", label="g(x)") # Plotten der Funktion f(x) im Intervall [a,b] plt.plot(x_interval,np.log(x_interval)+5, color="green", label="h(x)") # Plotten der Funktion f(x) im Intervall [a,b] y_interval=np.linspace(x_interval[-1]**3, data[-1,1]**3, int(data[-1,0])+1) # y-Bereich zum Veranschaulichen der unterschiedlichen Intervalle for i in data[:,0]: # Schleife um die einzelnen Resultate der Nullstelle Bisektion zu plotten index=int(i) # Umwandlung des Laufindex in eine Integer Zahl plt.plot([data[index,4],data[index,5]],[y_interval[index],y_interval[index]], color="red") # Plotten des i-ten Intervalls plt.scatter(data[index,1],y_interval[index], marker='*', color="black", s=25) # Plotten des i-ten p-Wertes plt.legend(frameon=True, loc="lower right",fontsize=10) # Anordnung der Legende plt.savefig("A4_1.png", bbox_inches="tight") # Speichern der Abbildung als Bild plt.show() # Zusaetzliches Darstellen der Abbildung in einem separaten Fenster
Musterlösung zur Aufgabe 2 (7.5 Punkte)
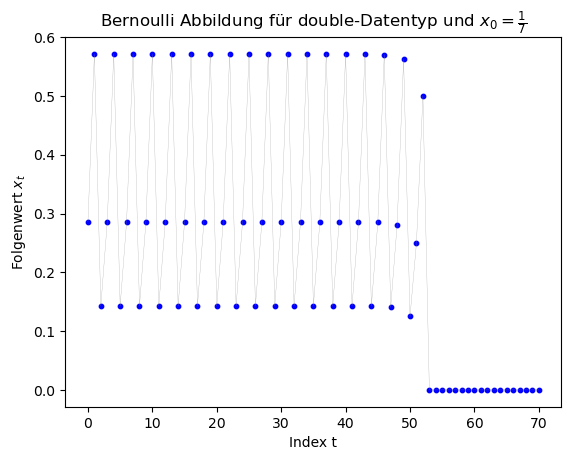
Das folgende C++ Programm stellt eine Musterlösung zur Aufgabe 2 dar, wobei ein double-Datentyp verwendet und die Folge mit $x_0 = \frac{1}{7}$ initialisiert wurde.
// Musterloesung der Aufgabe 2 des Uebungsblattes Nr.4 /* Die Bernoulli Abbildung, numerische Fehler schaukeln sich auf * Ausgabe zum Plotten (Gnuplot oder Python) mittels: "./a.out > Bernoulli.dat" */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) int main(){ // Hauptfunktion const unsigned int N = 70; // Definition der Anzahl Folgenglieder double x = 1.0/7.0; // Definition des Folgenwertes als double Zahl x in [0,1) // Initialisierung auch mit 1.0/3.0, 1.0/11.0, 1.0/101.0 und pow(2,-20) // Definition auch als float-Datentyp: float x = 1.0/7.0; printf("# 0: Folgenindex t \n# 1: Wert der Folge x_t \n"); // Beschreibung der ausgegebenen Groessen for(int t=0; t<=N; ++t){ // for-Schleife ueber die Folgenwerte if( x < 0.5 ){ // Falls x in [0,0.5) , dann ... x = 2.0*x; // ... multipliziere mit 2 } else{ // sonst (x in [0.5,1) , dann ... x = 2.0*x -1.0; // ... multipliziere mit 2 und ziehe 1 ab } // else Ende printf("%4i %20.15f \n",t, x); // Ausgabe des Folgenindex und des Folgenwertes } // Ende der for-Schleife } // Ende Hauptfunktion
Zum Visualisieren der Daten wurde das folgende Python-Skript verwendet:
# Python Programm zum Plotten der berechneten Daten von (Bernoulli.cpp) import matplotlib.pyplot as plt # Python Bibliothek zum Plotten (siehe https://matplotlib.org/ ) import numpy as np # Python Bibliothek fuer Mathematisches (siehe https://numpy.org/ ) data = np.genfromtxt("./Bernoulli.dat") # Einlesen der berechneten Daten von Bernoulli.cpp plt.title(r'Bernoulli Abbildung für $x_0=\frac{1}{7}$') # Titel der Abbildung plt.ylabel(r'Folgenwert $x_t$') # Beschriftung y-Achse plt.xlabel('Index t') # Beschriftung x-Achse plt.plot(data[:,0],data[:,1], color="grey", linewidth=0.2, alpha=0.7) # Plotten der Daten plt.scatter(data[:,0],data[:,1],c="blue", s=10) # Plotten der Daten plt.savefig("Bernoulli.png", bbox_inches="tight") # Speichern der Abbildung als Bild plt.show() # Zusaetzliches Darstellen der Abbildung in einem separaten Fenster
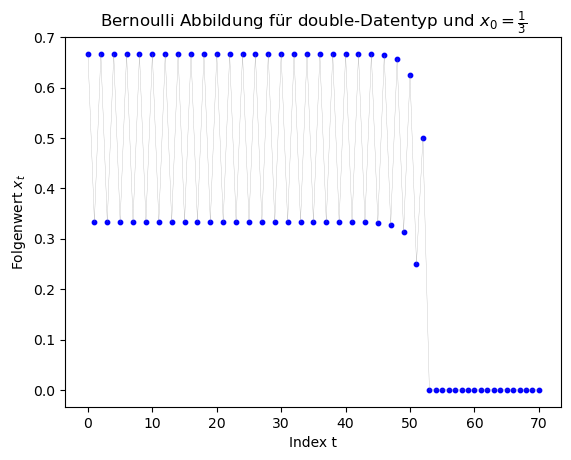
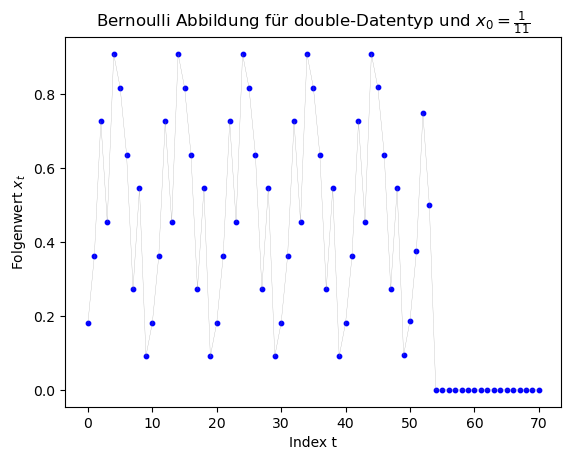
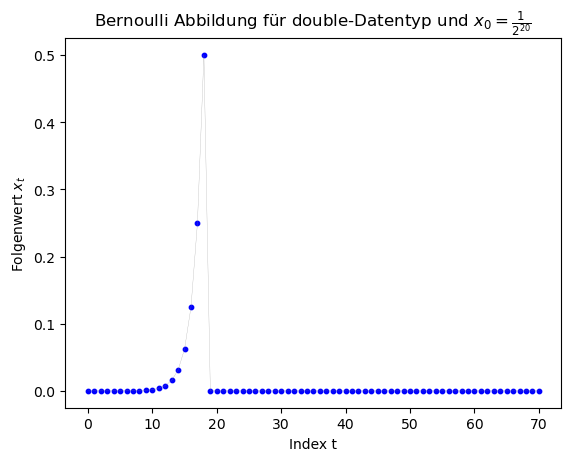
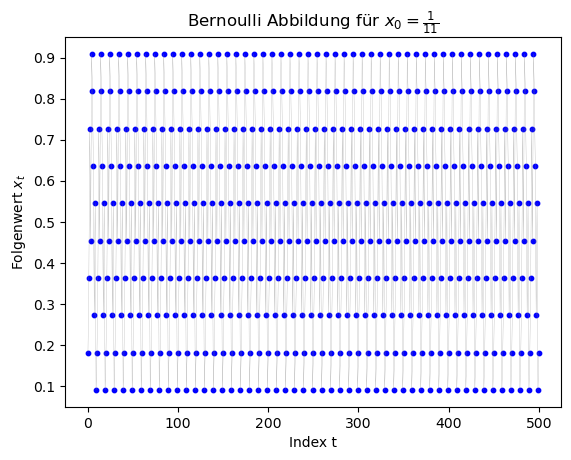
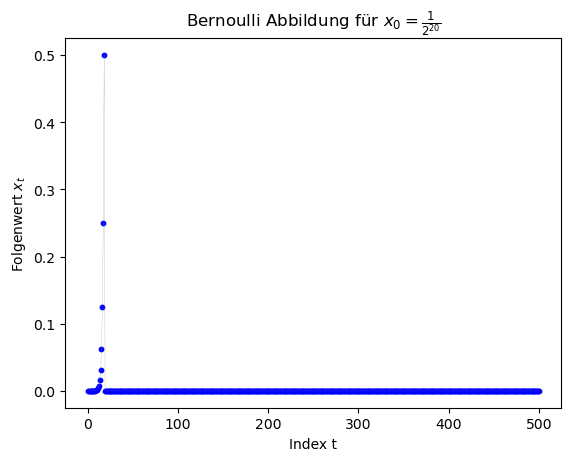
Die folgenden Grafiken zeigen die Ergebnisse des double-Datentyp mit den Startwerten $x_0 \in \{ \frac{1}{3}, \frac{1}{7}, \frac{1}{11}, \frac{1}{2^{20}} \}$.
Die weiteren Grafiken zeigen die entsprechenden Ergebnisse des float-Datentyps.
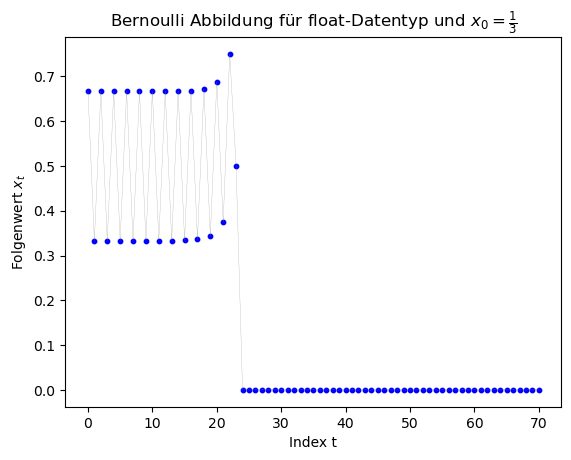
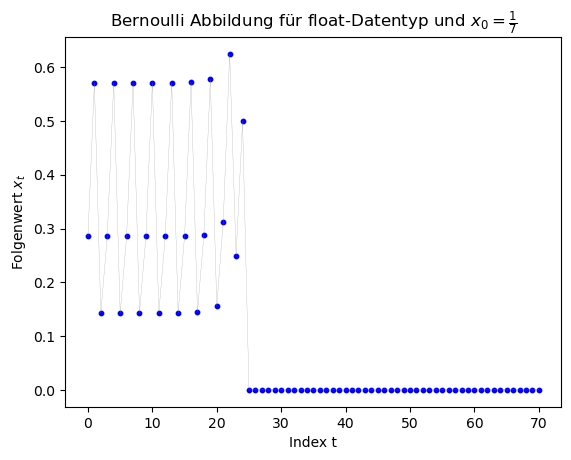
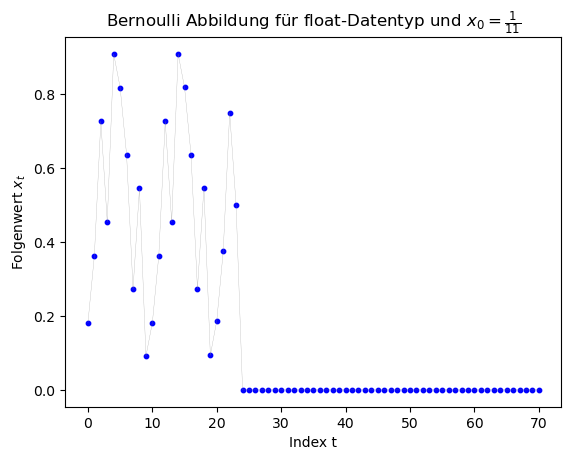
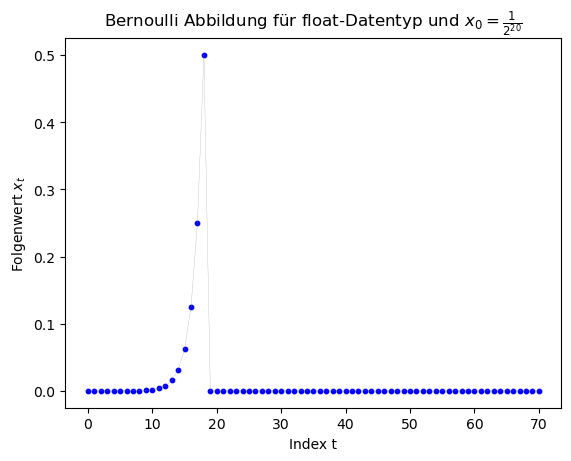
Betrachtet man sich die Grafiken, so erkennt man, dass (abgesehen von den Berechnungen mit $x_0 = \frac{1}{2^{20}} $ die Ergebnisse ab einem gewissen Folgenindex falsch sind, da für $x_0 \in \{ \frac{1}{3}, \frac{1}{7}, \frac{1}{11} \}$ die Folge periodische Lösungen hätte liefern sollen. Die Folge hätte z.B. für $x_0 = \frac{1}{7}$ die Werte $x_1 = \frac{2}{7}$, $x_2 = \frac{4}{7}$, $x_3 = \frac{1}{7}$, ... liefern sollen. Am Anfang stimmen die Werte auch, dann aber schaukeln sich die numerischen Fehler immer weiter auf und die Periodizität geht verlohren. Für den double-Datentyp geschiet dies bei ca. $t \approx 50$ und bei dem float-Datentyp schon bei ca. $t \approx 25$.
Da diese Rundungsfehler aufgrund der Computerarithmetik bei jeder Computerberechnung mit reellen Zahlen auftritt, muss man die mathematische Beschreibung der Bernoulli Abbildung in die natürliche Zahlenmenge überführen. \[ \begin{equation} x_{t+1} = \frac{m_{t+1}}{n} = \left\{ \begin{array}[c]{cl} 2 x_t = \frac{2 m_{t}}{n} \quad &\forall \,\, 2 m_t < n\\ 2 x_t - 1 = \frac{2 m_{t}}{n} - 1 = \frac{2 m_{t} -n }{n} \quad &\forall \,\, 2 m_t \geq n \end{array} \right. \qquad \quad \forall \,\, t \in ℕ \,\, \hbox{und} \,\, m_0 \in \{0,1,2,... \}\, , \,\, n \in \{1,2,... \} \, , \,\, m_0 < n \end{equation} \] Das folgende C++ Programm stellt die Implementierung dieser mathematischen Umformulierung der Bernoulli Abbildung dar.
// Musterloesung der Aufgabe 2 des Uebungsblattes Nr.4 /* Die Bernoulli Abbildung, Folgenwert wird als Bruch definiert, numerische Fehler schaukeln sich nicht mehr auf * Ausgabe zum Plotten (Gnuplot oder Python) mittels: "./a.out > Bernoulli.dat" */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) int main(){ // Hauptfunktion const unsigned int N = 500; // Definition der Anzahl Folgenglieder unsigned int m = 1; // Definition des Zaelers des Folgenwertes m = {0,1,2,3,...} unsigned int n = 7; // Definition des Nenners des Folgenwertes n = {1,2,3,...}, m < n printf("# 0: Folgenindex t \n# 1: Wert der Folge x_t \n"); // Beschreibung der ausgegebenen Groessen for(int t=0; t<=N; ++t){ // for-Schleife ueber die Folgenwerte if( 2*m < n ){ // Falls x=m/n in [0,0.5) , dann ... m = 2*m; // ... multipliziere mit 2 } else{ // sonst (x=m/n in [0.5,1) , dann ... m = 2*m - n; // ... multipliziere mit 2 und ziehe 1 ab } // else Ende printf("%4i %20.15f \n",t, double(m)/n); // Ausgabe des approximierten Wertes } // Ende der for-Schleife } // Ende Hauptfunktion
Die folgenden Grafiken zeigen die nun richtigen Ergebnisse des Programms, wobei jeweils 500 Folgenglieder berechnet wurden.
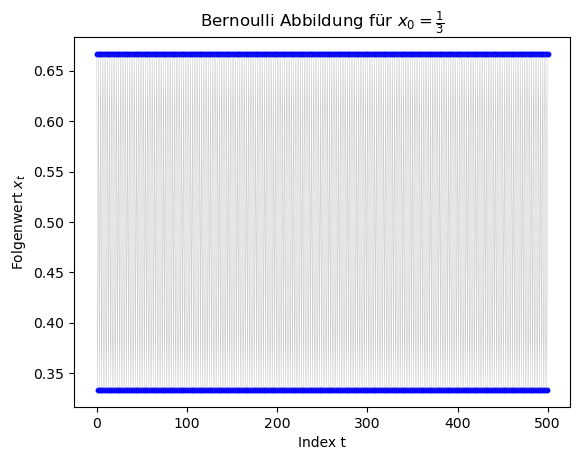
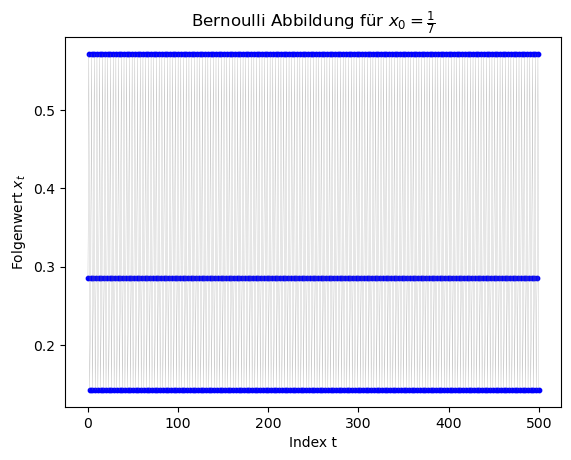
Musterlösung zur Aufgabe 3 (5 Punkte)
Die folgenden Ausdrücke wurden mittels eines C++ Programms berechnet.
\[
\begin{equation}
\prod_{k=1}^{11} k^2 \quad,\quad \sum_{k=0}^{20} \sum_{i=0\\i \neq k}^{10} \frac{k + i^3}{\left( k - i \right)^2} \quad,\quad \hbox{Bestimmen Sie N}\quad:\quad \sum_{k=0}^{N} \sum_{i=0\\i \neq k}^{250} \left( k + i^2 \right) = 672013120
\end{equation}
\]
Die Lösungen der ersten und dritten Aufgabe können hierbei nur ganzzahlige Werte annehmen, sodass lediglich die Lösung der zweiten Aufgabe auf 15 Stellen genau und die der ersten und dritten Aufgabe als Integerzahlen ausgegeben wurden.
Im Folgenden wird das entsprechende C++ Programm dargestellt:
// Musterlösung der Aufgabe 3 des Übungsblattes Nr.4 #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) int main(){ // Hauptfunktion int k, i; // Deklaration der Summenindexe long A_1 = 1; // Deklaration der long Variable für Aufgabe 3.1 und Initialisierung double A_2 = 0; // Deklaration der double Variable für Aufgabe 3.2 und Initialisierung long A_3 = 0; // Deklaration der long Variable für Aufgabe 3.3 und Initialisierung for(k=1; k<=11; ++k){ // Schleifen Anfang A_1 = A_1 * k*k; // Produkt 1 } // Schleifen Ende for(k=0; k<=20; ++k){ // Schleifen Anfang der 1.Summe for(i=0; i<=10; ++i){ // Schleifen Anfang der 2.Summe if( i != k ){ // if-Anweisung Anfang A_2 = A_2 + (k + pow(i,3))/pow(k - i,2); //Innerer, math. Teil der Doppelsumme } // if-Anweisung Ende } // Schleifen Ende der 2.Summe } // Schleifen Ende der 1.Summe k=0; while( A_3 != 672013120 ){ // Schleifen Anfang 1.Summe, mit Abbruchbedingung for(i=0; i<=250; ++i){ // Schleifen Anfang der 2.Summe if( i != k ){ // if-Anweisung Anfang A_3 = A_3 + (k + i*i); //Innerer, math. Teil der Doppelsumme } // if-Anweisung Ende } // Schleifen Ende der 2.Summe ++k; // Erhöhung von k um eins wegen while-Schleife } // Schleifen Ende der 1.Summe // Terminal Ausgabe auf 15 Nachkommastellen printf("%-24s %-24s %-24s \n","Aufgabe 3.1","Aufgabe 3.2","Aufgabe 3.3, N="); printf("%-24li %-24.15f %-24i \n",A_1,A_2,k-1); }
Das obere Programm produziert die folgende Terminalausgabe:
