Musterlösung zum Übungsblatt Nr. 2
Musterlösung zur Aufgabe 1 (10 Punkte)
Das folgende C++ Programm stellt eine Musterlösung zur Aufgabe 1 dar:
// Musterlösung der Aufgabe 1 des Übungsblattes Nr.2, Version a (ohne M_El) #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <limits> // In dieser Bibliothek ist das Template std::numeric_limits enthalten using namespace std; // Benutze den Namensraum std int main(){ // Hauptfunktion float e_approx_1; // Deklaration der float Variable für den approximierten Wert der Zahl e double e_approx_2; // Deklaration der double Variable für den approximierten Wert der Zahl e unsigned long n = 10000; // Deklaration der langen ganzen Zahl Variable n und Initialisierung e_approx_1 = pow(1+1.0/n,n); // Berechnung des Folgengliedes bei gewähltem n und Übergabe des Wertes an die float Variable e_approx_2 = pow(1+1.0/n,n); // Berechnung des Folgengliedes bei gewähltem n und Übergabe des Wertes an die double Variable const long double MY_E = 2.71828182845904523536L; // Definition der long double Konstanten des "wirklichen Wertes" von e // Terminal Ausgabe printf("Die Approximationen der Eulerschen Zahl e, unter Verwendung von n = %li, lauten: \n",n); printf("%24s %24s \n","float-Approximation","double-Approximation"); printf("%24.20f %24.20f \n",e_approx_1, e_approx_2); // Terminal Ausgabe der appr. Werte für e printf("%24s %24s \n","Fehler float","Fehler double"); printf("%24.20Lf %24.20Lf \n",MY_E - e_approx_1, MY_E - e_approx_2); // Terminal Ausgabe der Fehler printf("%24.16Le %24.16Le \n\n",MY_E - e_approx_1, MY_E - e_approx_2); // Fehler in exponentieller Schreibweise // Neuer, größerer Wert von n, neue Berechnung, Terminal Ausgabe n = 1.0e+8; //Entspricht n=10^8 e_approx_1 = pow(1+1.0/n,n); e_approx_2 = pow(1+1.0/n,n); // Terminal Ausgabe printf("Die Approximationen der Eulerschen Zahl e, unter Verwendung von n = %li, lauten: \n",n); printf("%24s %24s \n","float-Approximation","double-Approximation"); printf("%24.20f %24.20f \n",e_approx_1, e_approx_2); // Terminal Ausgabe der appr. Werte für e printf("%24s %24s \n","Fehler float","Fehler double"); printf("%24.20Lf %24.20Lf \n",MY_E - e_approx_1, MY_E - e_approx_2); // Terminal Ausgabe der Fehler printf("%24.16Le %24.16Le \n\n",MY_E - e_approx_1, MY_E - e_approx_2); // Fehler in exponentieller Schreibweise /* Neuer, größerer Wert von n, neue Berechnung, Terminal Ausgabe * Das Maschinen-Epsilon eines Gleitkommazahlen-Typs stellt die Differenz zwischen 1 und dem kleinsten darstellbaren Wert größer als 1 dar. * Da innerhalb der Folge (1+1/n)^n bei sehr großem n eine Zahl zu 1 addiert wird, die kleiner als das Maschinen-Epsilon ist, markiert * die ganze Zahl 1/epsilon die Zahl, bei der wohl die beste Approximation vorliegt */ n = 1.0/numeric_limits<double>::epsilon(); e_approx_1 = pow(1+1.0/n,n); e_approx_2 = pow(1+1.0/n,n); // Terminal Ausgabe printf("Die Approximationen der Eulerschen Zahl e, unter Verwendung von n = %li, lauten: \n",n); printf("%24s %24s \n","float-Approximation","double-Approximation"); printf("%24.20f %24.20f \n",e_approx_1, e_approx_2); // Terminal Ausgabe der appr. Werte für e printf("%24s %24s \n","Fehler float","Fehler double"); printf("%24.20Lf %24.20Lf \n",MY_E - e_approx_1, MY_E - e_approx_2); // Terminal Ausgabe der Fehler printf("%24.16Le %24.16Le \n",MY_E - e_approx_1, MY_E - e_approx_2); // Fehler in exponentieller Schreibweise }
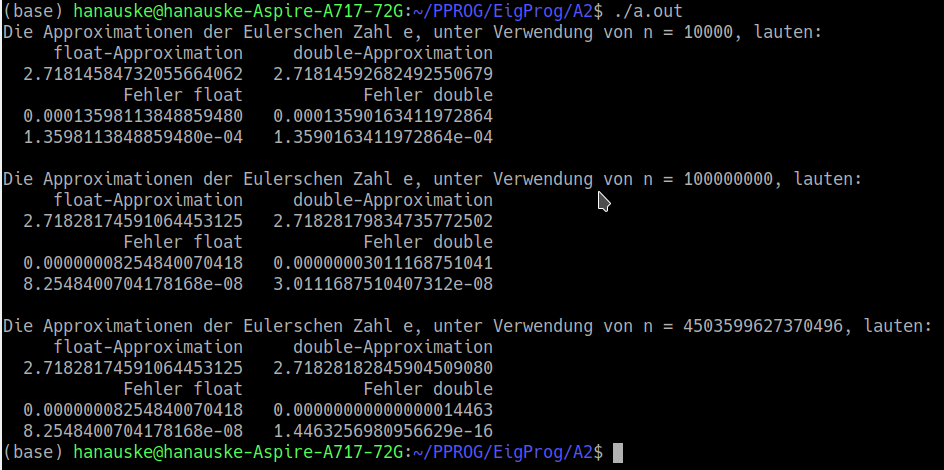
Zunächst werden die nötigen Bibliotheken eingebunden, wobei man <iostream> für die Ausgabe, <cmath> für mathematische Definitionen (z.B. den Wert der Eulerschen Zahl e) und <limits> für definierte numerische Grenzwerte (näheres siehe später) benötigt. Die darauf folgende Zeile ( using namespace std; ) benötigt man nicht für die Ausgabe, sondern das später, in <limits> enthaltene Template "numeric_limits" ist ein Teil des Namensraums "std". Danach werden die zwei reellwertige Variablen der Datentypen float und double deklariert, die die zwei approximierten Werte der Eulerschen Zahl $e$ darstellen sollen ("e_approx_1" und "e_approx_2"). Dann wird die lange natürliche Zahl $n$ deklariert und gleichzeitig mit dem Wert $10000$ initialisiert. Den zwei reellwertigen Variablen wird dann der Zahlenwert der Folge $\left( 1 + \frac{1}{n} \right)^n$ zugewiesen und die berechneten Werte werden in einer formatierten Ausgabe auf 20 Nachkommastellen genau ausgegeben. Zusätzlich wird auch der Fehler (${\cal F} = e - e_{approx}$) in normaler Kommaschreibweise und exponentieller Schreibweise ausgegeben. Dann wird der Wert von n auf $n = 10^8$ erhöht und die neu berechneten Werte werden wieder ausgegeben. Man erkennt (siehe später in der Terminalausgabe des ausgeführten Programms), dass die approximierten Werte der Eulerschen Zahl bei diesem erhöhten $n$ besser werden und der Fehler kleiner wird.
Wie genau kann man die Zahl $e$ mittels der definierten double-Variablen bestimmen? Man könnte nun denken, dass man einfach die größt mögliche Zahl für $n$ benutzt, da sich ja der exakte Wert von e im Limes $\lim \limits_{n \to \infty}$ ergibt. Die größt mögliche long Zahl beträgt $n_{max}:=9223372036854775807$, jedoch setzt man diese für $n$ ein und berechnet die approximierten Werte für e, erhält man keine sinnvollen Ergebnisse (man erhält als approximierte Werte nicht e, sondern 1). Dies liegt daran, dass innerhalb der Folge $a_n = \left( 1 + \frac{1}{n} \right)^n$ bei sehr großem $n$ eine Zahl zu 1 addiert wird, die kleiner als das Maschinen-Epsilon $\epsilon_M$ des double-Typs ist. Das Maschinen-Epsilon $\epsilon_M$ eines Gleitkommazahlen-Typs stellt die Differenz zwischen 1 und dem kleinsten darstellbaren Wert größer als 1 dar. Zwar ist der Zahlenwert $\frac{1}{n_{max}} = 1.08420217248550443401 \cdot 10^{-19}$ mittels einer double Variable ohne weiteres darstellbar (der kleinste Wert, der mit einer double-Variable darstellbar ist beträgt $2.22507385850720138309 \cdot 10^{-308}$), jedoch ist dieser kleiner als das Maschinen-Epsilon des double-Typs ($\epsilon_M=2.22044604925031308085 \cdot 10^{-16}$). Dies bewirkt nun, das der Ausdruck $\left( 1 + \frac{1}{n_{max}} \right)$ die Zahl 1 zurückgibt und die Potenz $1^{n_{max}}$ ändert daran auch nichts mehr. Nun versteht man, dass wohl die beste Approximation der Zahl e durch folgenden Ausdruck zu programmieren ist: $ \left( 1 + \epsilon_M \right)^\frac{1}{\epsilon_M}$. Die wohl beste natürliche Zahl ergibt sich somit durch den ganzzahligen Wert der Zahl $\frac{1}{\epsilon_M}$, was im nebenstehenden Programm durch die Zeile "n = 1.0/numeric_limits<double>::epsilon();" ausgedrückt wurde (der Wert für n berechnet sich zu $n=4503599627370495$). Kompiliert man das Programm und führt es im Terminal aus, so erhält man die links oben abgebildete Terminalausgabe.
Es sollte abschließend angemerkt werden, dass der berechnete Fehler nicht die Abweichung von der tatsächlichen Eulerschen Zahl e (ca. $2.7182818284590452353602874713526625...$) widerspiegelt, sondern die Differenz zwischen dem approximierten Wert und der selbst definierten long double-Konstanten MY_E (const long double MY_E = 2.71828182845904523536L;). Der wirklich in der Variable MY_E initialisierte Wert ist aufgrund der hardwareabhängigen Präzision von long double ein wenig anders ($2.71828182845904523543...$) und somit nur auf 18 Nachkommastellen genau. Hätte man hingegen den berechneten Fehler mittels der Differenz zwischen dem approximierten Wert und der schon vordefinierten double-Konstanten M_E berechnet, würde man bei der letzten Ausgabe eine Abweichung von exakt null erhalten, was fälschlicherweise suggeriert hätte, dass der Wert zu 100 Prozent genau ist. In der, auf den Rechnern des ITP installierten Compiler-Version g++, ist zusätzlich eine long double-Erweiterung von M_E verfügbar (M_El = 2.718281828459045235360287471352662498L). Diese Konstante M_El ist eine GNU-spezifische Erweiterung der verwendeten Compiler-Version und wird implizit über die Header-Datei <cmath> bereitgestellt, die intern <math.h> einbindet, wo M_E und M_El definiert sind. Das Programm A2_1.cpp benutzt diese long double-Konstante M_El anstatt der selbst definierten Konstante MY_E und gibt die gleichen Größen wie in der oberen Musterlösung aus. Aufgrund der hardwareabhängigen Präzision unterscheiden sich die Terminalausgaben der beiden Programme jedoch nicht voneinander. Benutzt man hingegen eine neue Compiler-Version mit einer Standard-Bibliothek C++20 oder höher, so kann man die <numbers>-Header-Datei verwenden, um einen long double-Wert von $e$ mittels 'numbers::e_v<long double>' zu definieren (siehe Programm A2_1b.cpp); dieser ist jedoch wieder nur 18 Nachkommastellen genau und unterscheidet sich effektiv somit nicht von M_El oder MY_E.
Musterlösung zur Aufgabe 2 (5 Punkte)
Das folgende C++ Programm berechnet die mathematischen Ausdrücke
und gibt sie dann auf 10 und 20 Stellen genau im Terminal mittels einer formatierten Ausgabe aus. Die Zahlenwerte wurden zunächst in sechs double-Variablen (doppelte Maschinengenauigkeit) gespeichert und danach mittels printf(..) ausgegeben.
// Musterloesung der Aufgabe 2 des Uebungsblattes Nr.2 #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) int main(){ // Hauptfunktion double A_1 = 64.0/128; // Deklaration der double Variable für Aufgabe 2.1 und Initialisierung double A_2 = 1.0/3; // Deklaration der double Variable für Aufgabe 2.2 und Initialisierung double A_3 = 2*M_PI/5; // Deklaration der double Variable für Aufgabe 2.3 und Initialisierung double A_4 = cos(M_PI/2); // Deklaration der double Variable für Aufgabe 2.4 und Initialisierung double A_5 = exp(pow(5.84,-12)); // Deklaration der double Variable für Aufgabe 2.5 und Initialisierung double A_6 = log(exp(1.1)); // Deklaration der double Variable für Aufgabe 2.6 und Initialisierung // Terminal Ausgabe auf 10 bzw. 20 Nachkommastellen printf("%-24s %-24s %-24s %-24s %-24s %-24s \n","Aufgabe 2.1","Aufgabe 2.2","Aufgabe 2.3","Aufgabe 2.4","Aufgabe 2.5","Aufgabe 2.6"); printf("%-24.10f %-24.10f %-24.10f %-24.10f %-24.10f %-24.10f \n",A_1,A_2,A_3,A_4,A_5,A_6); printf("%-24.20f %-24.20f %-24.20f %-24.20f %-24.20f %-24.20f \n",A_1,A_2,A_3,A_4,A_5,A_6); }
Kompiliert man das Programm und führt es im Terminal aus, so erhält man die unten abgebildete Terminalausgabe.

// Aufgabe 3 des Übungsblattes Nr.2 // Drei Fehler und viele unschöne Ausdrücke #include <iostream> #include <cmath> int main(){ int n; n = 0; double a = 0; a = pow(2,n); cout < a << endl; n = n + 1; a = pow(n,2); cout << a << endl; n = n + 1; a = pow(n,2); cout << a << endl; n = n + 1; a = pow(n,2); cout << a << endl; }
// Aufgabe 3 des Übungsblattes Nr.2 // Drei Fehler wurden korrigiert #include <iostream> #include <cmath> using namespace std; // 1. Fehler int main(){ int n; n = 0; double a = 0; a = pow(n,2); // 2. Fehler cout << a << endl; // 3. Fehler n = n + 1; a = pow(n,2); cout << a << endl; n = n + 1; a = pow(n,2); cout << a << endl; n = n + 1; a = pow(n,2); cout << a << endl; }
// Musterlösung: Aufgabe 3 des Übungsblattes Nr.2 #include <iostream> using namespace std; int main(){ unsigned int n =0; cout << n*n << endl; ++n; cout << n*n << endl; ++n; cout << n*n << endl; ++n; cout << n*n << endl; }
Musterlösung zur Aufgabe 3 (5 Punkte)
Das ursprüngliche fehlerhafte Programm (linke Abbildung) lässt sich nicht kompilieren. Der erste Fehler liegt darin, dass der Ausgabebefehl "cout" verwendet wurde, ohne zuvor kenntlich zu machen, dass dieser sich im Namensraum der Standardbibliothek "std" befindet. Der zweite Fehler liegt in einer falschen Verwendung der Potenzfunktion. "pow(2,n)" bedeutet $2^n$ und nicht $n^2$. Der dritte Fehler liegt bei der erstmaligen Verwendung des Befehls "cout" (ein Kleinerzeichen zu wenig). Das auf der rechten Seite dargestellte Programm stellt die fehlerkorrigierte Version dar, und dieses lässt sich nun kompilieren und liefert nach der Ausführung auch richtige Ergebnisse (die Zahlenwerte der Folge $(a_n)_{n \in ℕ}$ mit $a_n := n^2$ für $n \in [0,1,2,3]$ werden richtig ausgegeben). Das Programm ist jedoch immer noch an vielen Stellen umständlich und nicht optimal programmiert. So kann man z.B. die getrennte Deklaration und Initialisierung der Variable $n$ in einer Zeile schreiben und es ist wohl genauer diese Variable als unsigned int-Typ zu deklarieren, da sie keine negativen Werte annehmen kann. Bei einer Berechnung von $n^2$ ist es vielleicht nicht unbedingt notwendig die "pow()"-Funktion zu verwenden und man kann einfach "n*n" schreiben; dies ist aber sicherlich eine Geschmacksache. Die verwendeten Inkrementierungen der Zahl n (n = n + 1;) ist zwar nicht falsch, aber schöner ist sicherlich die Verwendung des Inkrementierungsoperators "++n;". Die untere linke Abbildung zeigt eine Version eines verbesserten Programms.