Musterlösung zum Übungsblatt Nr. 11
Musterlösung zur Aufgabe 1 (20 Punkte)
Im folgenden C++ Header File SchwingendeKette_Klasse.hpp ist die Subklasse 'Kette' von der abstrakten Klasse 'dsolve' abgeleitet. Mittels der Klasse 'Kette' lassen sich Simulationen einer schwingenden Kette bestehend aus einer beliebigen Anzahl von Perlen mit unterschiedlichen Massen erstellen.
/* Header-Datei * Die schwingende Kette mit beliebiger Anzahl von Perlen * ist ein Beispiel eines schwingenden, gekoppelten Massensystems aus dem Bereich der Mechanik * Berechnung der Lösung eines Systems von Differentialgleichungen * mittels Runge-Kutta Ordnung vier Methode * Verfahren zur Loesung der DGL ist in einer abstrakten Basisklasse ausgelagert * Berechnung der Lösung innerhalb einer Methode (Klassenfunktion) Runge-Kutta-Verfahren * Überschreibung der virtuellen Funktion der Bewegungsgleichungen in der abgeleiteten Klasse (Subklasse) Kette * Zeitentwicklung der fuer unterschiedliche t-Werte in [a,b] * Unterklasse Kette * Konstruktor: Kette(Fadenspannung T,Abständ zwischen Perlen a0, Massenvektor der Perlen, Anfangszeit a, Endzeit b, Anzahl der Punkte N, Anfangswerte alpha) */ #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <vector> // Vector-Container der Standardbibliothek using namespace std; // Benutze den Namensraum std // Abstrakte Basisklasse 'dsolve' class dsolve { public: // Daten-Member der Klasse double a; // Untergrenze des Zeit-Intervalls double b; // Obergrenze des Intervalls int N; // Anzahl der Punkte vector<double> alpha; // Anfangswerte vector<vector<double>> ym; // Lösungsmatrix vector<double> t; // Zeit-Vektor // Virtuelle Funktion dgls, wird an anderer Stelle definiert virtual vector<double> dgls(double t, vector<double> u_vec) = 0; // Konstruktor mit vier Argumenten (Initialisierung der Daten-Member) dsolve(double a_, double b_, int N_, vector<double> alpha_) :a(a_), b(b_), N(N_), alpha(alpha_) { t.push_back(a_); // Zum Zeit-Vektor die Anfangszeit eintragen ym.push_back(alpha_); // Zur Loesungs-Matrix die Anfangswerte eintragen } // Methode der Runge-Kutta-Methode void solve() { double h = (b - a)/N; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) int n = alpha.size(); // Anzahl der Anfangswerte bzw. DGL-Gleichungen (hier n=2) vector<double> k1(n),k2(n),k3(n),k4(n); // Deklaration der vier Runge-Kutta Parameter fuer jede Loesung vector<double> y(n); // Temporaerer Hilfsvektor for (int i = 0; i < N; ++i) { // for-Schleife ueber die einzelnen Punkte des t-Intervalls for (int j = 0; j < n; ++j) k1[j] = h * dgls(t[i], ym[i])[j]; // for-Schleife ueber die n Runge-Kutta k1-Parameter for (int j = 0; j < n; ++j) y[j] = ym[i][j] + k1[j] / 2; // Temporaerer Hilfsvektor for (int j = 0; j < n; ++j) k2[j] = h * dgls(t[i] + h / 2, y)[j]; // for-Schleife ueber die n Runge-Kutta k2-Parameter for (int j = 0; j < n; ++j) y[j] = ym[i][j] + k2[j] / 2; // Temporaerer Hilfsvektor for (int j = 0; j < n; ++j) k3[j] = h * dgls(t[i] + h / 2, y)[j]; // for-Schleife ueber die n Runge-Kutta k3-Parameter for (int j = 0; j < n; ++j) y[j] = ym[i][j] + k3[j]; // Temporaerer Hilfsvektor for (int j = 0; j < n; ++j) k4[j] = h * dgls(t[i] + h, y)[j]; // for-Schleife ueber die n Runge-Kutta k4-Parameter for (int j = 0; j < n; ++j) y[j] = ym[i][j] + (k1[j] + 2 * k2[j] + 2 * k3[j] + k4[j]) / 6; // Temporaerer Hilfsvektor ym.push_back(y); // Zum Loesungs-Vektor den neuen Wert eintragen t.push_back(a + (i + 1) * h); // Zum Zeit-Vektor die neue Zeit eintragen } // Ende for-Schleife ueber die einzelnen Punkte des t-Intervalls } // Ende des Methode 'solve()' }; // Ende der Klasse 'dsolve' // Sub-Klasse 'Kette' class Kette : public dsolve { public: double T; // Fadenspannung T double a0; // Aequidistante Abstaenden zwischen den Perlen vector<double> m; // Vektor der Massen der Perlen unsigned anz_p; // Anzahl der Perlen // Überschreibung der virtuellen Funktion dgls // Definition der Bewegungsgleichung der schwingenden Kette bestehend aus anz_p Perlen vector<double> dgls(double t, vector<double> u_vec){ vector<double> du_dt; // Die 2*anz_p DGLs erster Ordnung werden als Standard-Vektor definiert for(unsigned i=0; i < anz_p; ++i){ // Erster Block von anz_p DGLs erster Ordnung du_dt.push_back(u_vec[anz_p+i]); // ... } // ... du_dt.push_back(T/(m[0]*a0)*(u_vec[1] - 2*u_vec[0])); // Zweiter Block von anz_p DGLs erster Ordnung for(unsigned i=anz_p+1; i < 2*anz_p-1; ++i){ // ... mit Bewegungsgleichungen du_dt.push_back(T/(m[i-anz_p]*a0)*(u_vec[i-anz_p-1] - 2*u_vec[i-anz_p] + u_vec[i-anz_p+1])); } // ... du_dt.push_back(T/(m[anz_p-1]*a0)*(u_vec[anz_p-2]-2*u_vec[anz_p-1])); // ... return du_dt; // Rueckgabewert der DGLs als Standard-Vektor } // Ende: Definition der Bewegungsgleichung-Funktion // Konstruktor mit sieben Argumenten (Initialisierung der Instanzvariablen (T,a0,m), vier Argumente für dsolve) Kette(double T_ = 1.0, double a0_ = 1.0, vector<double> m_ = {1,1}, double a_ = 0, double b_ = 1, int N_ = 10, vector<double> alpha_ = {0.1,0,0,0}) : dsolve(a_, b_, N_, alpha_), T(T_), a0(a0_), m(m_) {anz_p = static_cast<unsigned>(m_.size());} // Methode der Ausgabe der Orte der Perlen am Stützpunkt i vector<double> r(size_t i) { vector<double> w(anz_p,0.0); if (i < t.size()) { for(unsigned j=0; j < anz_p; ++j){ w[j] = ym[i][j]; } } return w; } // Methode der Ausgabe der Geschwindigkeiten der Perlen am Stützpunkt i vector<double> v(size_t i) { vector<double> w(anz_p,0.0); if (i < t.size()) { for(unsigned j=0; j < anz_p; ++j){ w[j] = ym[i][j+anz_p]; } } return w; } }; // Ende der Unterklasse 'Kette'
Die eigentliche Instanzbildung des Objektes der Klasse 'Kette' und die konkrete Berechnung der Aufgabenteile wurde mittels der folgenden C++ Datei angefertigt. Es wurden sowohl die drei Eigenschwingungen einer Kette bestehend aus drei Perlen der Massen $m_1=1$, $m_2=2$ und $m_3=3$ berechnet und mit den entsprechenden Python-Simulationen verglichen, als auch ein System bestehend aus 10 Perlen unterschiedlicher Massen simuliert.
/* Die schwingende Kette mit beliebiger Anzahl von Perlen * ist ein Beispiel eines schwingenden, gekoppelten Massensystems aus dem Bereich der Mechanik * Berechnung der Lösung eines Systems von Differentialgleichungen * mittels Runge-Kutta Ordnung vier Methode * Verfahren zur Loesung der DGL ist in einer abstrakten Basisklasse ausgelagert * Berechnung der Lösung innerhalb einer Methode (Klassenfunktion) Runge-Kutta-Verfahren * Überschreibung der virtuellen Funktion der Bewegungsgleichungen in der abgeleiteten Klasse (Subklasse) Kette * Zeitentwicklung der fuer unterschiedliche t-Werte in [a,b] * Unterklasse Kette * Konstruktor: Kette(Fadenspannung T,Abständ zwischen Perlen a0, Massenvektor der Perlen, Anfangszeit a, Endzeit b, Anzahl der Punkte N, Anfangswerte alpha) * * Ausgabe zum Plotten mittels Python Jupyter Notebook A11_1.ipynb: "./a.out > Kette_3P_e1.dat */ #include "SchwingendeKette_Klasse.hpp" // Header-Datei der schwingenden Kette mit beliebiger Anzahl von Perlen #include <iostream> // Standard Input- und Output Bibliothek in C, z.B. printf(...) using namespace std; // Hauptfunktion int main(){ double T=1; // Fadenspannung T double a0=1; // Aequidistante Abstaenden zwischen den Perlen vector<double> m {1,2,3}; // Vektor der Massen der drei Perlen vector<double> u_init {1,1,-1,0,0,0}; // Anfangswerte (Orte und Geschwindigkeiten der drei Perlen); 1. Eigenschwingung // vector<double> u_init {7-2*sqrt(10),sqrt(10)-2,1,0,0,0}; // Anfangswerte 2. Eigenschwingung // vector<double> u_init {(7+2*sqrt(10))*0.1,-(sqrt(10)+2)*0.1,0.1,0,0,0}; // Anfangswerte 3. Eigenschwingung // vector<double> m {1,2,3,4,5,6,7,8,9,10}; // Vektor der Massen der 10 Perlen // vector<double> u_init {0,0,0,0,0,0,0,0,0,0,1,1.0/2,1.0/3,1.0/4,1.0/5,1.0/6,1.0/7,1.0/8,1.0/9,1.0/10}; // Anfangswerte 10 Perlen double a = 0; // Untergrenze des Zeit-Intervalls double b = 20; // Obergrenze des Intervalls int N = 100000; // Anzahl der Punkte Kette K_A = Kette(T,a0,m,a,b,N,u_init); // Konstruktor bilded eine Instanz der Klasse Kette Pendel K_A.solve(); // Methode des Runge-Kutta-Verfahrens ausführen printf("# 0: Index i \n# 1: t-Wert \n# 2:y_1 \n# 3:v_1 \n# 4:y_2 \n# 5:v_2 \n# 6:y_3 ... \n"); // Beschreibung der ausgegebenen Groessen for(size_t i=0; i < K_A.t.size(); ++i){ // for-Schleife über die Zeitgitterpunkte printf("%3ld %19.15f ",i,K_A.t[i]); // Ausgabe Index und Zeit for(unsigned j=0; j < K_A.anz_p; ++j){ // for-Schleife zur Terminalausgabe; anz_p-Perlen printf("%19.15f %19.15f ",K_A.r(i)[j],K_A.v(i)[j]); // Ausgabe y-Wert und Geschwindigkeit der Perle j } // Ende der for-Schleife; anz_p-Perlen printf("\n"); // Neue Zeile } // Ende der for-Schleife; Zeitgitterpunkte } // Ende der Hauptfunktion
Berechnung und Darstellung der Eigenschwingungen einer Kette bestehend aus drei Perlen
In dem Jupyter Notebook A11_1.ipynb (View Notebook, Download Notebook) wurden die Eigenschwingungen analytisch berechnet und die Ergebnisse der C++ und Python Simulationen sind auch dort ausführlich dargestellt. Die erstellten Simulationsergebnisse des C++ Programms sind in der folgenden '.zip'-Datei zusammengefasst Kette-C++.zip. Es folgen die Animationen der Simulationen der drei Eigenschwingungen.
Die rechte untere Abbildung vergleicht die Ergebnisse der C++ und Python Simulationen, für die dritte Eigenschwingung (Abbildung links unten), miteinander.
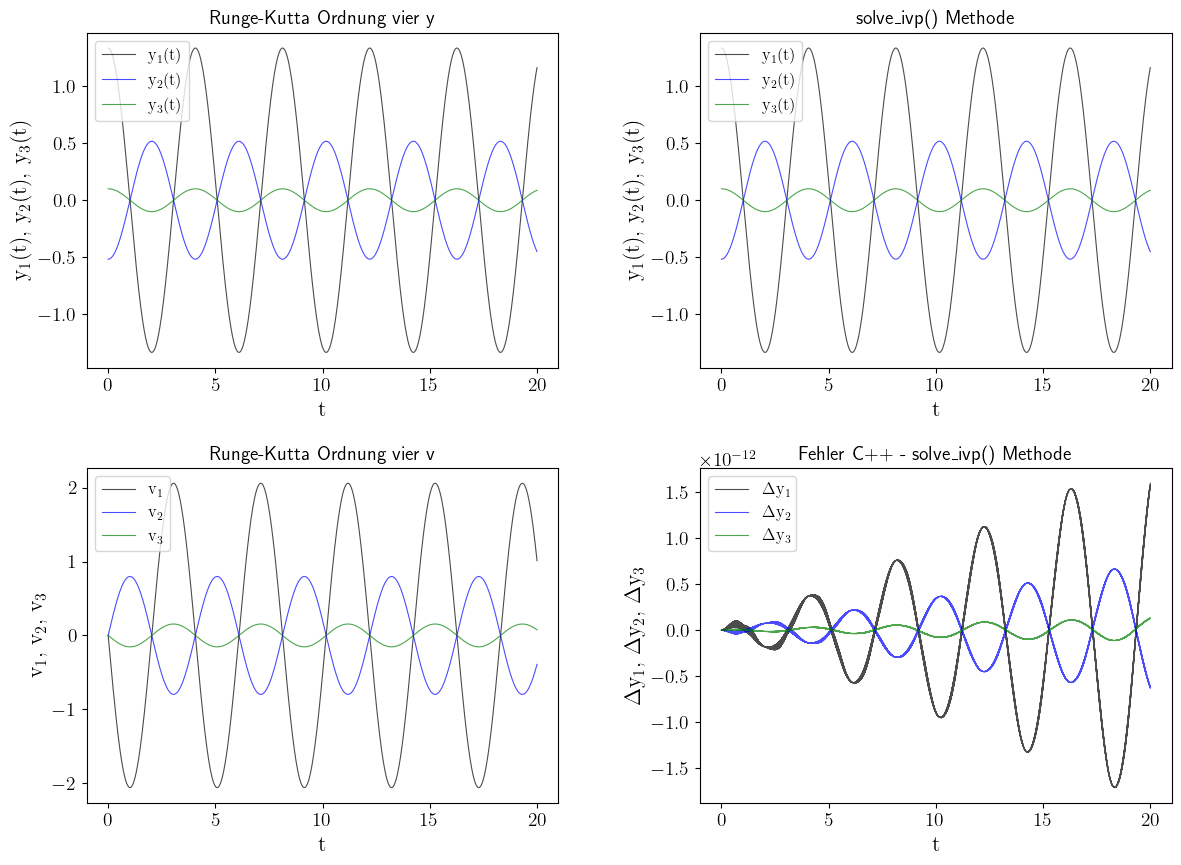
Zusammengefasst kann man sagen, dass die Python und C++ Simulationen mit drei Perlen sehr gut miteinander übereinstimmen.
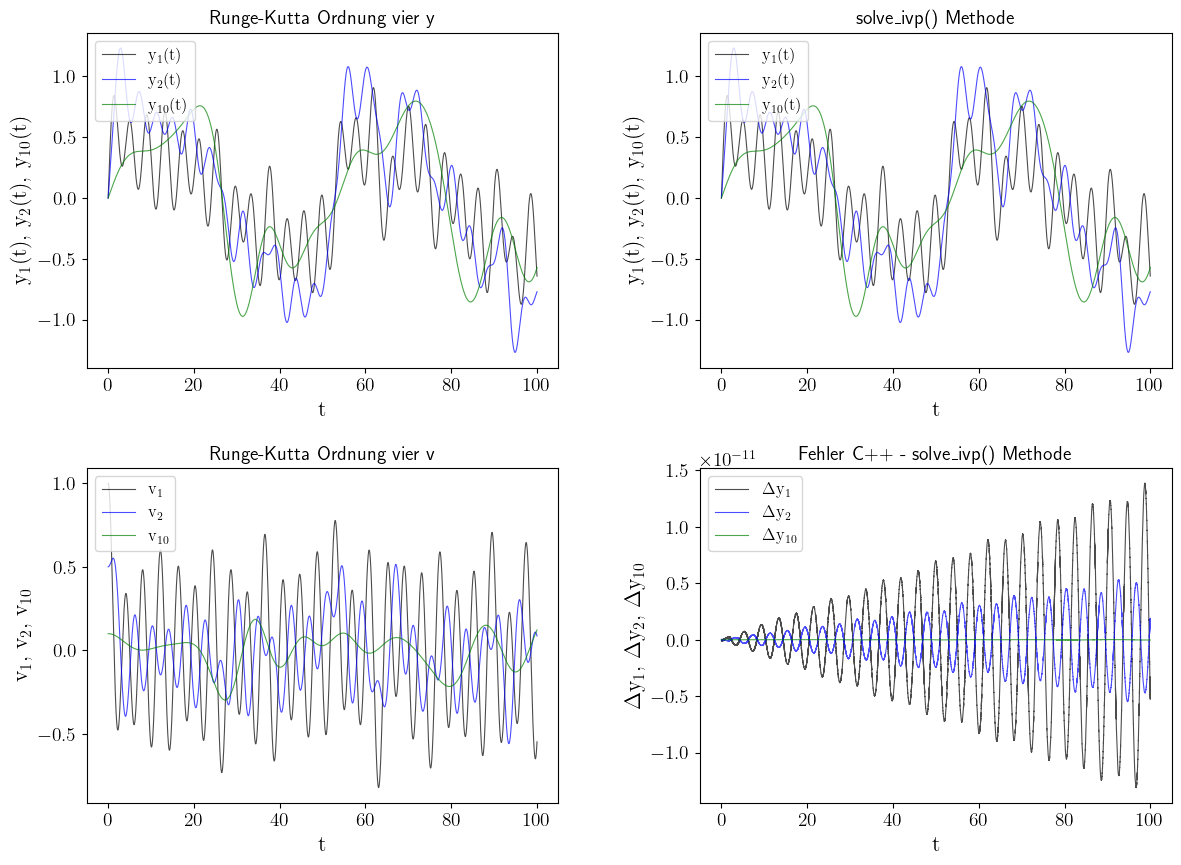
10 Perlen mit unterschiedlichen Massen
Wir betrachten nun eine Kette bestehend aus 10 Perlen mit ansteigenden Massenwerten ($m_1=1, m_2=2, ..., m_{10}=10$). Zum Anfangszeitpunkt $t=0$ werden die Perlen aus ihrer Ruhelage wie folgt angestoßen: $\frac{d y_1(0)}{dt} = \frac{1}{1}, \frac{d y_2(0)}{dt} = \frac{1}{2}, ..., \frac{d y_{10}(0)}{dt} = \frac{1}{10}$. Die Abbildung auf der rechten Seite vergleicht die Python Simulation mit den Ergebnissen des C++ Programmes und stellt, der Übersichtlichkeit halber nur die Bewegungen der ersten, zweiten und 10. Perle dar. Auch hier stimmen die Ergebnisse der Python und C++ Simulationen sehr gut miteinander übereinstimmen. Die untere Animation zeigt die entstehende Perlenbewegung der Kette bestehend aus 10 Perlen.
100 Perlen mit unterschiedlichen Massen
Wir betrachten nun eine Simulation mit $n=100$ Perlen und unterschiedlicher Massenwerte. Die Massenwerte der Perlen sollen sich dabei wieder wie folgt über die Kette verteilen $m_1=1, m_2=2, ..., m_{100}=100$). Die Anfangsauslenkung der Kette sei so gewählt, dass sie im mittleren Bereich in positive Richtung wie eine Gauß-Verteilung ausgelenkt sei und die Perlen zum Zeitpunkt $t=0$ nicht angestoßen werden. Die untere Abbildung zeigt die Simulationsergebnisse in einer Animation.