Musterlösung zum Übungsblatt Nr. 10
Musterlösung zur Aufgabe 1 (20 Punkte)
Das folgende C++ Programm stellt eine Erweiterung des C++ Programms DGL_2.cpp auf ein System bestehend aus drei gekoppelten Differentialgleichungen erster Ordnung dar und löst das folgende Differentialgleichung-System des Lorenz-Modells: \begin{eqnarray} \dot{x}(t) &=& \frac{d x}{dt} = \, \sigma \cdot \left( y - x \right) \\ \dot{y}(t) &=& \frac{d y}{dt} = \, r \cdot x - y - x \cdot z \\ \dot{z}(t) &=& \frac{d z}{dt} = \, x \cdot y - b \cdot z \end{eqnarray} Der Einfachheit halber wurden die ursprünglichen Variablen-Namen beibehalten und die Variablen des Lorenz-Modells entsprechen nun den folgenden Programm-Variablen: $x:=y_1$, $y:=y_2$ und $z:=y_3$.
// Musterlösung der Aufgabe 1 des Übungsblattes Nr.10 // Numerische Lösung des Lorenz-Modells, mit x=y_1, y=y_2, z=y_3 /* Berechnung der Lösung eines Systems von drei gekoppelten Differentialgleichung * der Form y1'=f1(t,y1,y2,y3) , y2'=f2(t,y1,y2,y3), , y3'=f2(t,y1,y2,y3) * mittels der Euler Methode und Runge-Kutta Ordnung vier Methode * Zeitentwicklung von y1(t), y2(t), y3(t) der fuer unterschiedliche t-Werte in [a,b] * Ausgabe zum Plotten mittels Python Jupyter Notebook A10_2.ipynb: "./a.out > Lorenz-r_28-init_0.dat */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) double f_1(double t, double y_1, double y_2, double y_3){ // Deklaration und Definition der Funktion f_1(t,y1,y2,y3) double wert; wert = 10.0*(y_2 - y_1); // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f_1 } // Ende der Funktion f_1 double f_2(double t, double y_1, double y_2, double y_3){ // Deklaration und Definition der Funktion f_2(t,y1,y2,y3) double wert; double r = 28.0; wert = r * y_1 - y_2 - y_1*y_3; // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f_2 } // Ende der Funktion f_2 double f_3(double t, double y_1, double y_2, double y_3){ // Deklaration und Definition der Funktion f_3(t,y1,y2,y3) double wert; wert = y_1*y_2 - 8.0/3.0 * y_3; // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f_3 } // Ende der Funktion f_3 int main(){ // Hauptfunktion double a = 0; // Untergrenze des Zeit-Intervalls [a,b] in dem die Loesung berechnet werden soll double b = 50; // Obergrenze des Intervalls [a,b] int N = 100000; // Anzahl der Punkte in die das t-Intervall aufgeteilt wird double h = (b - a)/N; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) double alpha_1 = 0; // 1.Anfangswert bei t=a: y_1(a)=alpha_1 double alpha_2 = 1; // 2.Anfangswert bei t=a: y_2(a)=alpha_2 double alpha_3 = 0; // 2.Anfangswert bei t=a: y_3(a)=alpha_3 double t; // Aktueller Zeitwert double y_Euler_1 = alpha_1; // Deklaration und Initialisierung der numerischen Loesung der Euler Methode fuer y_1 double y_RungeK_4_1 = alpha_1; // Deklaration und Initialisierung der numerischen Loesung der Runge-Kutta Ordnung vier Methode double k1_1,k2_1,k3_1,k4_1; // Deklaration der vier Runge-Kutta Parameter fuer y_1 double y_Euler_2 = alpha_2; // Deklaration und Initialisierung der numerischen Loesung der Euler Methode fuer y_2 double y_RungeK_4_2 = alpha_2; // Deklaration und Initialisierung der numerischen Loesung der Runge-Kutta Ordnung vier Methode double k1_2,k2_2,k3_2,k4_2; // Deklaration der vier Runge-Kutta Parameter fuer y_2 double y_Euler_3 = alpha_3; // Deklaration und Initialisierung der numerischen Loesung der Euler Methode fuer y_3 double y_RungeK_4_3 = alpha_3; // Deklaration und Initialisierung der numerischen Loesung der Runge-Kutta Ordnung vier Methode double k1_3,k2_3,k3_3,k4_3; // Deklaration der vier Runge-Kutta Parameter fuer y_3 double tmp_1,tmp_2; // Variablen zum Zwischenspeichern von Ergebnissen printf("# 0: Index i \n# 1: t-Wert \n# 2: Euler Methode y1 \n# 3: Euler Methode y2 \n"); // Beschreibung der ausgegebenen Groessen printf("# 4: Euler Methode y3 \n# 5: Runge-Kutta Ordnung vier y1 \n"); // Beschreibung der ausgegebenen Groessen printf("# 6: Runge-Kutta Ordnung vier y2 \n# 7: Runge-Kutta Ordnung vier y3 \n"); // Beschreibung der ausgegebenen Groessen for(int i=0; i <= N; ++i){ // for-Schleife ueber die einzelnen Punkte des t-Intervalls t = a + i*h; // Zeit-Parameter wird um h erhoeht printf("%3d %19.15f %19.15f %19.15f %19.15f ",i, t, y_Euler_1, y_Euler_2, y_Euler_3); // Ausgaben der Loesungen printf(" %19.15f %19.15f %19.15f \n", y_RungeK_4_1, y_RungeK_4_2, y_RungeK_4_3); // Ausgaben der Loesungen tmp_1 = y_Euler_1 + h*f_1(t,y_Euler_1,y_Euler_2,y_Euler_3); // Euler Methode tmp_2 = y_Euler_2 + h*f_2(t,y_Euler_1,y_Euler_2,y_Euler_3); y_Euler_3 = y_Euler_3 + h*f_3(t,y_Euler_1,y_Euler_2,y_Euler_3); // y_3 Euler Methode y_Euler_1 = tmp_1; // y_1 Euler Methode y_Euler_2 = tmp_2; // y_2 Euler Methode k1_1 = h*f_1(t,y_RungeK_4_1,y_RungeK_4_2,y_RungeK_4_3); // Runge-Kutta Parameter k1 fuer y_1 k1_2 = h*f_2(t,y_RungeK_4_1,y_RungeK_4_2,y_RungeK_4_3); // Runge-Kutta Parameter k1 fuer y_2 k1_3 = h*f_3(t,y_RungeK_4_1,y_RungeK_4_2,y_RungeK_4_3); // Runge-Kutta Parameter k1 fuer y_3 k2_1 = h*f_1(t+h/2,y_RungeK_4_1+k1_1/2,y_RungeK_4_2+k1_2/2,y_RungeK_4_3+k1_3/2); // Runge-Kutta Parameter k2 fuer y_1 k2_2 = h*f_2(t+h/2,y_RungeK_4_1+k1_1/2,y_RungeK_4_2+k1_2/2,y_RungeK_4_3+k1_3/2); // Runge-Kutta Parameter k2 fuer y_2 k2_3 = h*f_3(t+h/2,y_RungeK_4_1+k1_1/2,y_RungeK_4_2+k1_2/2,y_RungeK_4_3+k1_3/2); // Runge-Kutta Parameter k2 fuer y_3 k3_1 = h*f_1(t+h/2,y_RungeK_4_1+k2_1/2,y_RungeK_4_2+k2_2/2,y_RungeK_4_3+k2_3/2); // Runge-Kutta Parameter k3 fuer y_1 k3_2 = h*f_2(t+h/2,y_RungeK_4_1+k2_1/2,y_RungeK_4_2+k2_2/2,y_RungeK_4_3+k2_3/2); // Runge-Kutta Parameter k3 fuer y_2 k3_3 = h*f_3(t+h/2,y_RungeK_4_1+k2_1/2,y_RungeK_4_2+k2_2/2,y_RungeK_4_3+k2_3/2); // Runge-Kutta Parameter k3 fuer y_3 k4_1 = h*f_1(t+h,y_RungeK_4_1+k3_1,y_RungeK_4_2+k3_2,y_RungeK_4_3+k3_3); // Runge-Kutta Parameter k4 fuer y_1 k4_2 = h*f_2(t+h,y_RungeK_4_1+k3_1,y_RungeK_4_2+k3_2,y_RungeK_4_3+k3_3); // Runge-Kutta Parameter k4 fuer y_2 k4_3 = h*f_3(t+h,y_RungeK_4_1+k3_1,y_RungeK_4_2+k3_2,y_RungeK_4_3+k3_3); // Runge-Kutta Parameter k4 fuer y_3 y_RungeK_4_1 = y_RungeK_4_1 + (k1_1 + 2*k2_1 + 2*k3_1 + k4_1)/6; // Runge-Kutta Ordnung vier Methode fuer y_1 y_RungeK_4_2 = y_RungeK_4_2 + (k1_2 + 2*k2_2 + 2*k3_2 + k4_2)/6; // Runge-Kutta Ordnung vier Methode fuer y_2 y_RungeK_4_3 = y_RungeK_4_3 + (k1_3 + 2*k2_3 + 2*k3_3 + k4_3)/6; // Runge-Kutta Ordnung vier Methode fuer y_3 } // Ende for-Schleife ueber die einzelnen Punkte des t-Intervalls } // Ende der Hauptfunktion
Aufgrund der nicht-linearen Bewegungsgleichung des Lorenz-Modells können sich in gewissen Parameterbereichen kleine Ungenauigkeiten exponentiell vergrößern, sodass eine genaue Vorhersage der Bewegung nach einiger Zeit nicht mehr möglich ist. Bei $r=28$ entsteht z.B. ein chaotischer bzw. seltsamen Attraktor (Lorenz-Attraktor). Der Parameter $r$ kann per Hand innerhalb der Funktion 'double f_2(double t, double y_1, double y_2, double y_3){...}' festgelegt werden. In dem Jupyter Notebook A10.ipynb (View Notebook, Download Notebook) sind die Ergebnisse der C++ und Python Simulationen ausführlich für die folgenden unterschiedlichen r-Werte $r = 0.9, 12, 22, 28$ dargestellt. Im Folgenden werden nur einige Resultate exemplarisch dargestellt.
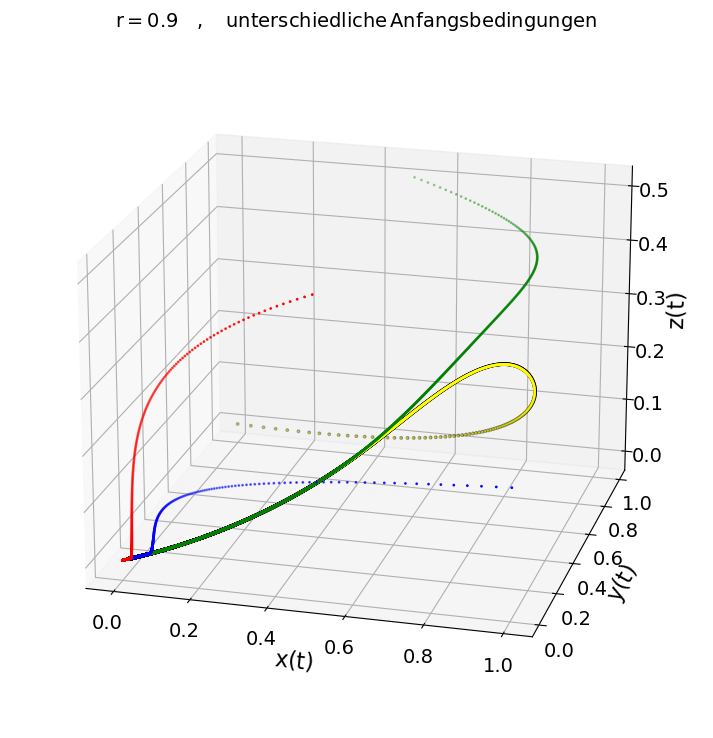
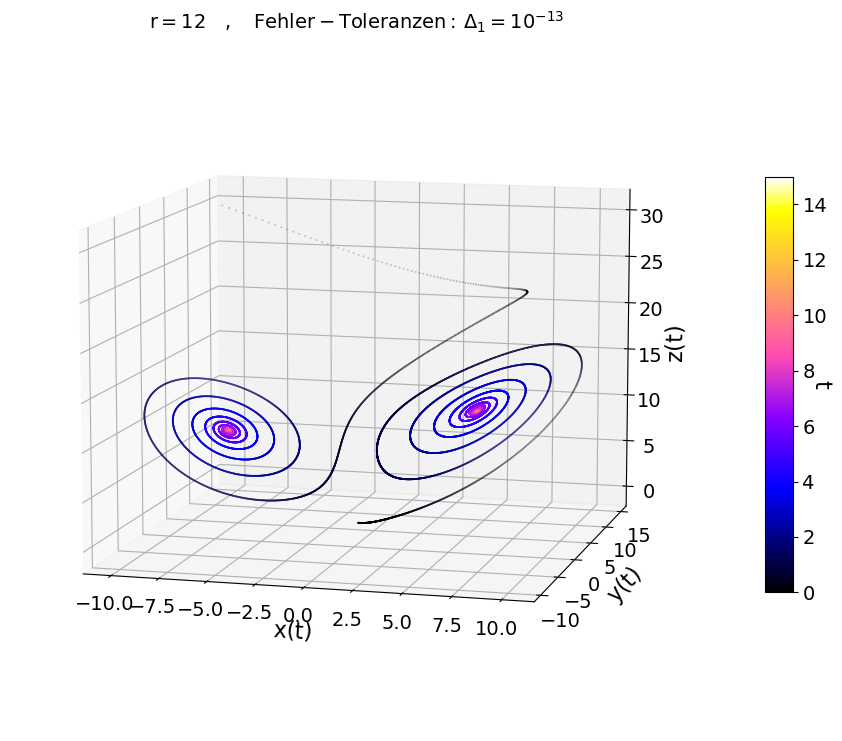
Für $r < 1$ entwickelt sich das System unabhängig von der Anfangsbedingung stets hin zu dem stabilen Fixpunkt (Attraktor) im Ursprung $[x,y,z] = [0,0,0]$ (siehe Abbildung links oben, $r=0.9$). Für $r=12$ existieren zwei stabile Attraktoren, zu welchen sich das System abhängig von der Anfangsbedingung entwickeln kann (siehe Abbildung rechts oben). Für $r=22$ gibt es ebenfalls zwei stabile Attraktoren, zu denen sich das System nach langer Zeit hin entwickeln wird. Jedoch gibt es auch Anfangsbedingungen, bei denen es in einem begrenzten zeitlichen Abschnitt zu einem vorübergehenden chaotischen Verhalten kommen kann ('transient chaos'). Die beiden unteren Abbildungen zeigen zwei Simulationen mit $r=22$ und nahezu den gleichen Anfangsbedingungen (links unten $[x(0),y(0),z(0)] = [20,12,-10]$ und rechts unten $[x(0),y(0),z(0)] = [20,11.999,-10]$).
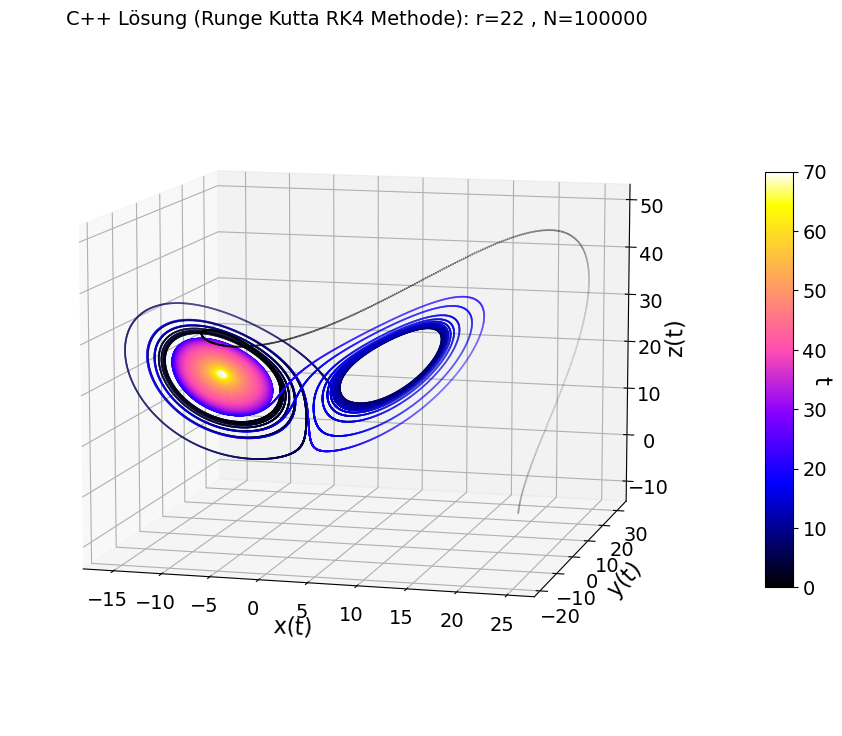
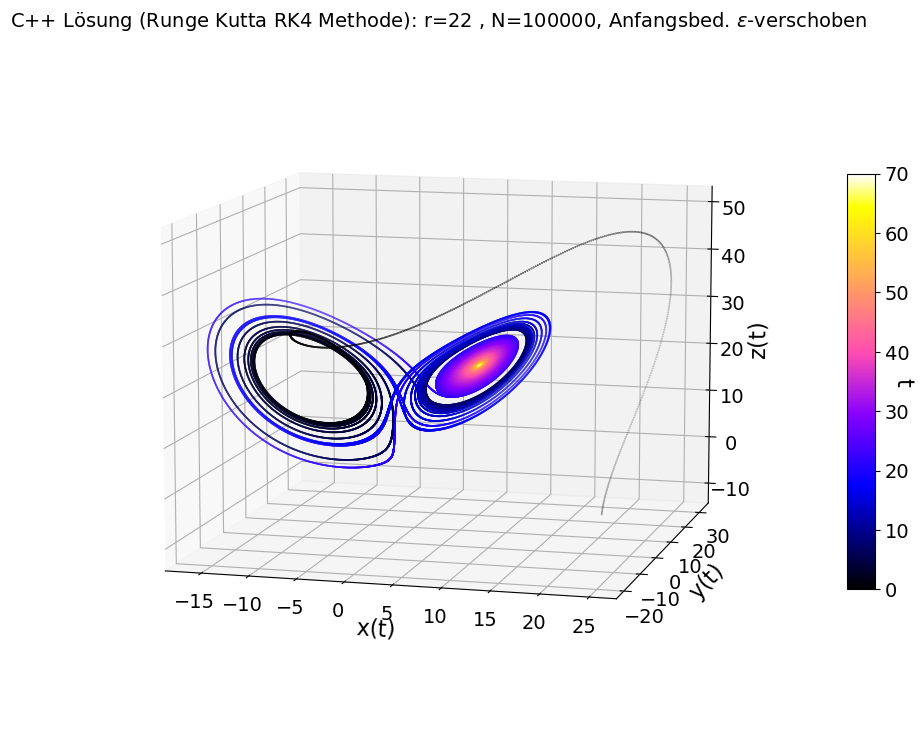
Die beiden Trajektorien zeigen klar, dass sich die Simulation der $\epsilon$-verschobene Anfangsbedingung zu einem anderen Fixpunkt entwickelt als die ursprüngliche. Diese Eigenschaft, dass kleine Veränderungen der Anfangsbedingungen die gesamte Entwicklung des Systems nach einiger Zeit verändern können, bezeichnet man als der "Schmetterlingseffekt" in der Chaostheorie. Die Abbildung unten links zeigt hingegen zwei Simulationen mit anderen Anfangsbedingungen für $r=22$ ($[x(0),y(0),z(0)] = [0,1,0]$ und $[x(0),y(0),z(0)] = [-10,12,30]$), bei denen es nicht zu einem vorübergehenden chaotischen Verhalten kommt.
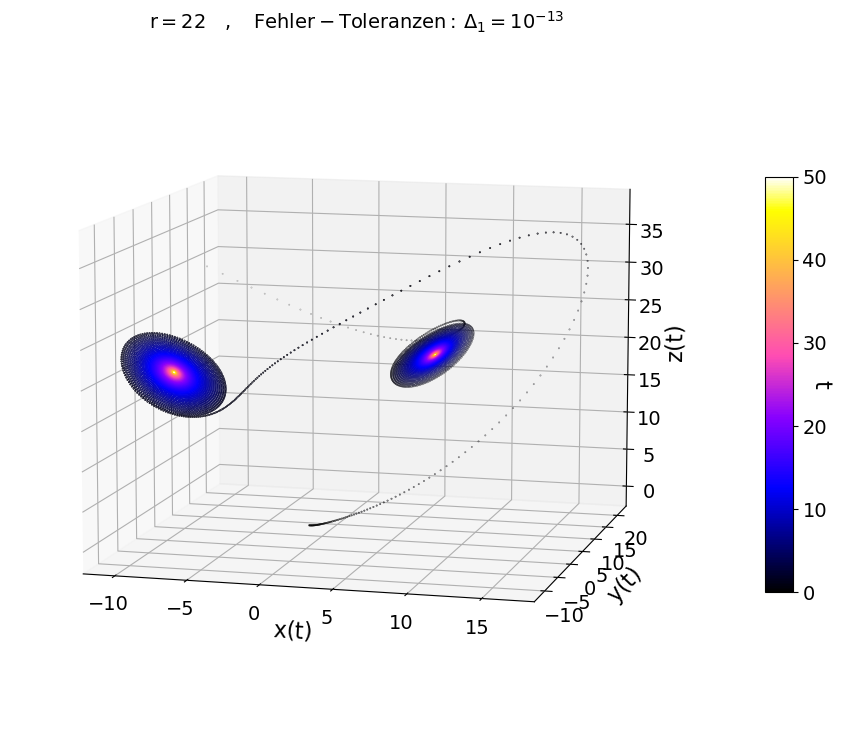
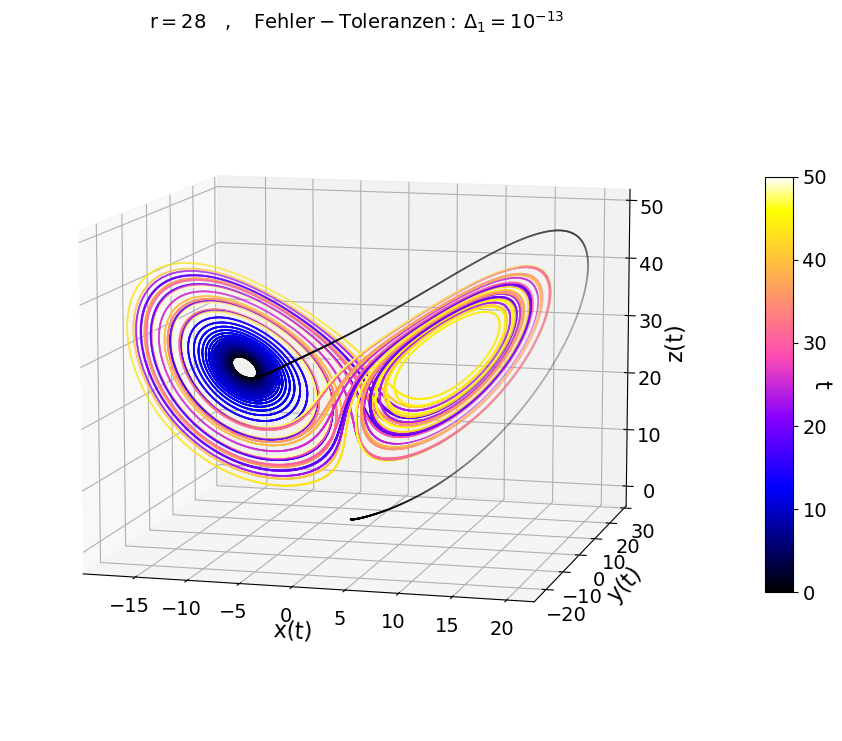
Für $r > r_H = \frac{\sigma \left( \sigma + b +3 \right)}{\sigma - b -1} \approx 24.74$ verhält sich das System jedoch weitgehend chaotisch und die Trajektorie der Systemfunktionen zeigt einen "seltsamen Lorenz-Attraktor" (siehe Abbildung oben rechts, $r=28$). Die Struktur dieses "seltsamen Attraktors" entwickelt sich dabei unabhängig von der speziellen Anfangsbedingung, wobei die genaue zeitliche Entwicklung der Trajektorie nach einer gewissen Zeit nicht mehr vorhersagbar ist (in der Abbildung unten links wurde z.B. der Anfangswert nur um einen $\epsilon$-Wert verändert, $[x(0),y(0),z(0)] = [0,0.999,0]$).
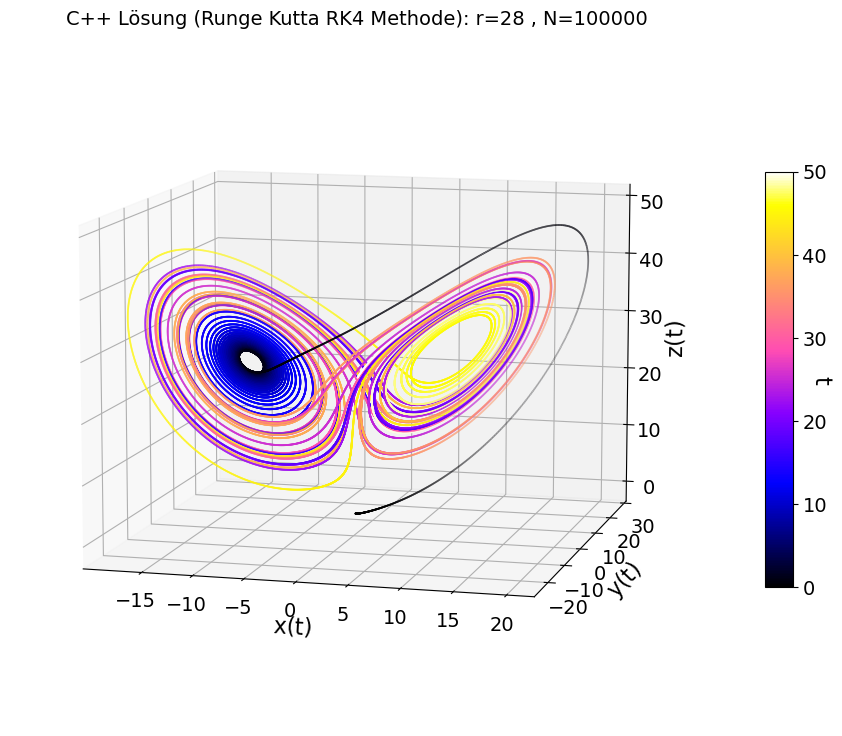
Stellt man sich die zeitliche Entwicklung der Systemfunktionen, mit den ursprünglichen Anfangsbedingungen, in einem gewöhnlichen zweidimensionalen Diagramm dar, so erhält man die folgende Abbildung.
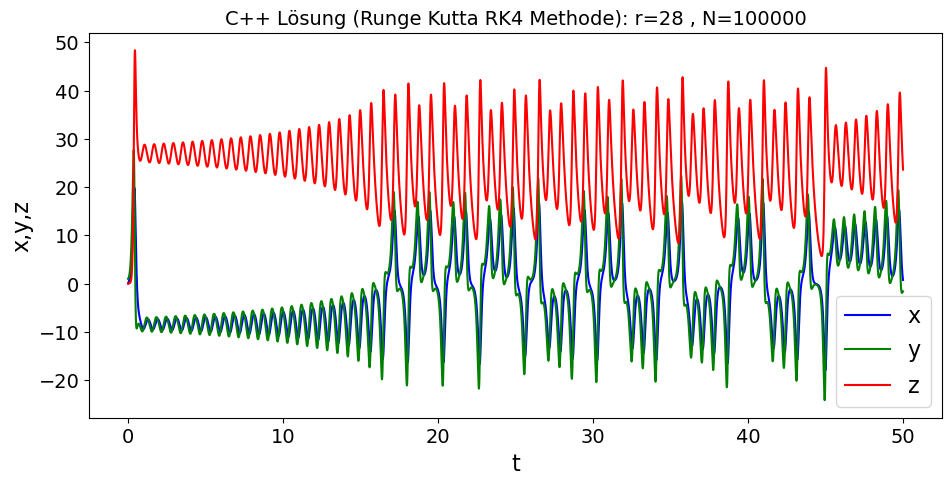
Man kann sich nun die zeitliche Entwicklung der Abweichungen $\Delta x$, $\Delta y$ und $\Delta z$ zur $\epsilon$-verschobenen Simulation in C++ und Python betrachten. Auch ist ein Vergleich der Ergebnisse der beiden unterschiedlichen Programme möglich. Die Ergebnisse zeigen, dass eine genaue Vorhersage der zeitlichen Entwicklung des Systems nach einer gewissen Zeit nicht mehr möglich ist.
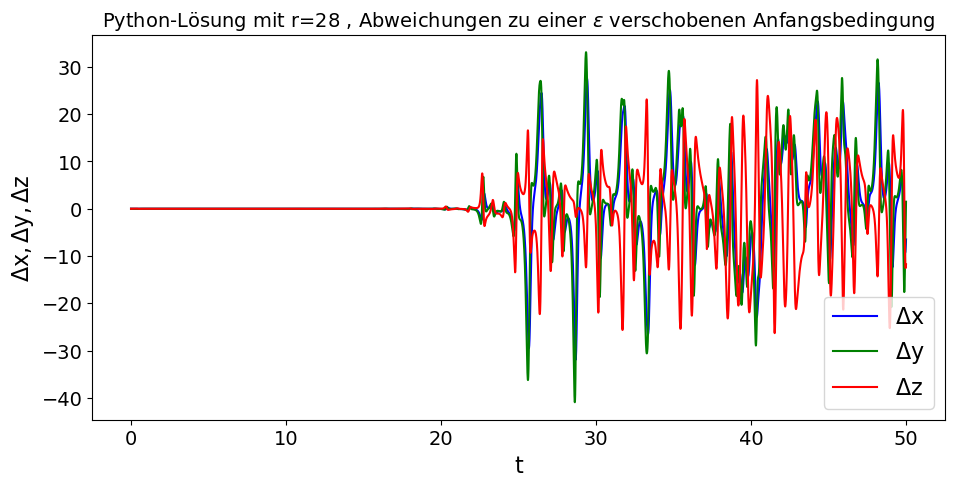
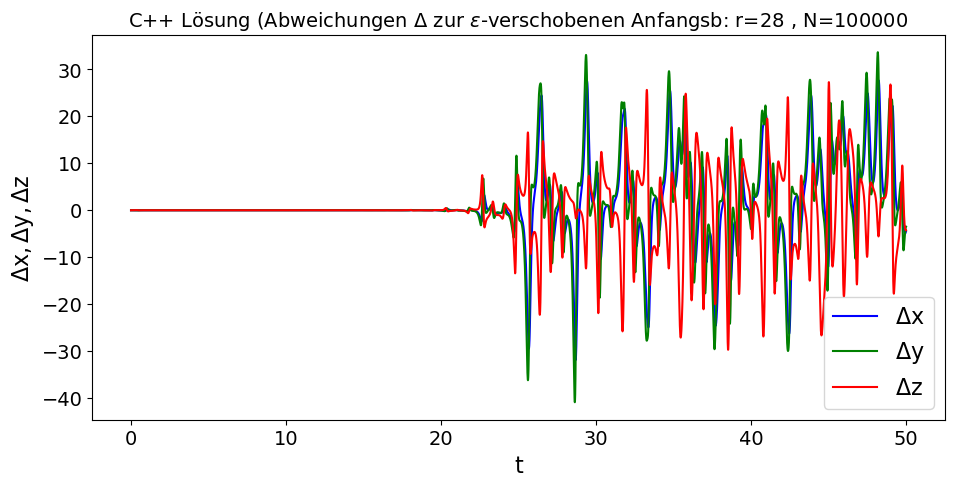
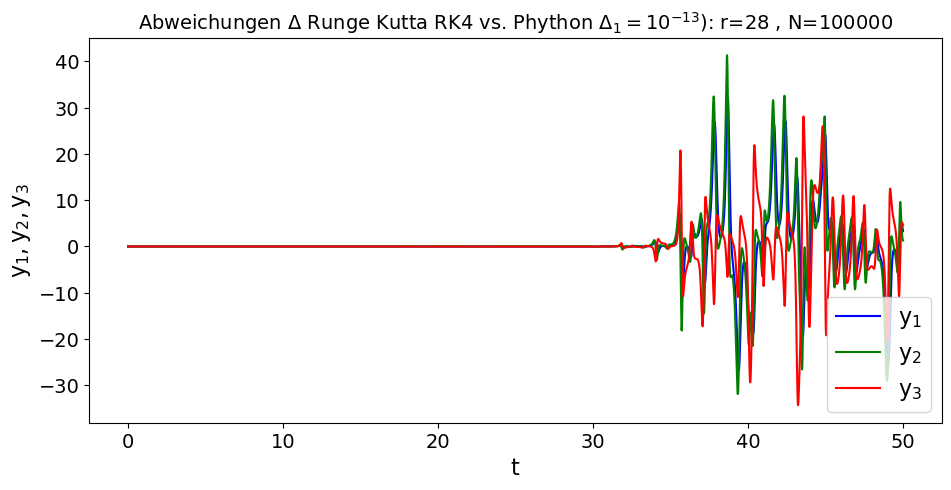
Für $r > r_H \approx 27.74$ treten somit chaotische Bewegungsformen auf. Die zeitliche Entwicklung von chaotischen Bewegungen ist nicht vorhersagbar und es ist bemerkenswert, dass ein solches Chaos überhaupt in deterministischen Gleichungen entstehen kann (deterministisches Chaos). Aufgrund der nicht-linearen Bewegungsgleichung des Lorenz-Modells können sich in gewissen Parameterbereichen kleine Ungenauigkeiten exponentiell vergrößern, sodass eine genaue Vorhersage der Bewegung nach einiger Zeit nicht mehr möglich ist; es entsteht ein chaotischer bzw. seltsamen Attraktor. Dies veranschaulichen die nebenstehenden Abbildungen.
In dem Jupyter Notebook A10.ipynb (View Notebook, Download Notebook) sind die Ergebnisse der C++ und Python Simulationen ausführlich dargestellt. Die erstellten Simulationsergebnisse des C++ Programms sind in der folgenden '.zip'-Datei zusammengefasst Lorenz-C++.zip.