Musterlösung zum Übungsblatt Nr. 9
Musterlösung zur Aufgabe 1 (10 Punkte)
Die Musterlösung ist am Beispiel des 'Runge-Kutta Ordnung vier'-Verfahrens aufgebaut. Das folgende C++ Programm zeigt zunächst eine Möglichkeit der Umformulierung des C++ Programmes DGL_1.cpp in eine Klassenstruktur, wobei als Klassenname 'dsolve' verwendet wurde.
// Musterlösung der Aufgabe 1a des Übungsblattes Nr.9 /* Berechnung der Lösung einer Differentialgleichung der Form y'=f(t,y) * mittels Runge-Kutta Ordnung vier Verfahren * Verfahren zur Loesung der DGL ist in eine Klasse ausgelagert * Zeitentwicklung der fuer unterschiedliche t-Werte in [a,b] * Kostruktor: dsolve(Anfangszeit a, Endzeit b, Anzahl der Punkte N, Anfangswert alpha=y(a)) */ #include <stdio.h> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <vector> // Vector-Container der Standardbibliothek using namespace std; // Benutze den Namensraum std class dsolve{ //Definition der Klasse 'dsolve' double a = 0; // Untergrenze des Zeit-Intervalls [a,b] in dem die Loesung berechnet werden soll double b = 2; // Obergrenze des Intervalls [a,b] int N = 10; // Anzahl der Punkte in die das t-Intervall aufgeteilt wird double h = (b - a)/N; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) double alpha = 0.5; // Anfangswert bei t=a: y(a)=alpha double t; // Aktueller Zeitwert double k1, k2, k3, k4; // Deklaration der vier Runge-Kutta Parameter vector<double> y_RungeK_4; // Deklaration eines double Vektors zum speichern der Loesung vector<double> Zeit; // Deklaration eines double Vektors zum speichern der Zeit-Werte public: // Konstruktor mit vier Argumenten (Initialisierung der Parameter, Berechnung der Loesung der DGL) dsolve(double a_, double b_, int N_, double alpha_) : a(a_),b(b_),N(N_),alpha(alpha_) { Zeit.resize(N_ + 1); // Die Anzahl der Eintraege im Vektor wird auf N+1 erhoeht y_RungeK_4.resize(N_ + 1); // Die Anzahl der Eintraege im Vektor wird auf N+1 erhoeht Zeit[0] = a_; // Zum Zeit-Vektor die Endzeit eintragen y_RungeK_4[0] = alpha_; // Zum y-Vektor den Anfangswert alpha_=y(a) eintragen for(int i=0; i < N; ++i){ // for-Schleife ueber die einzelnen Punkte des t-Intervalls k1 = h*f(t,y_RungeK_4[i]); // Runge-Kutta Parameter 1 k2 = h*f(t+h/2,y_RungeK_4[i] + k1/2); // Runge-Kutta Parameter 2 k3 = h*f(t+h/2,y_RungeK_4[i] + k2/2); // Runge-Kutta Parameter 3 k4 = h*f(t+h,y_RungeK_4[i] + k3); // Runge-Kutta Parameter 4 t = a + (i+1)*h; // Zeit wird um h erhoeht Zeit[i+1] = t; // Zum Zeit-Vektor die neue Zeit eintragen y_RungeK_4[i+1] = y_RungeK_4[i] + + (k1 + 2*k2 + 2*k3 + k4)/6; // Zum y-Vektor den neuen Wert eintragen } // Ende for-Schleife ueber die einzelnen Punkte des t-Intervalls }; // Ende des Konstruktors double f(double t, double y); // Deklaration der Member-Funktion f(t,y) (Definition findet ausserhalb der Klasse statt) double y_analytisch(double t, double alpha); // Deklaration der Member-Funktion f(t,alpha) (Definition findet ausserhalb der Klasse statt) const vector<double>& get_y() const { return y_RungeK_4; } // Definition der konstanten Member-Funktion get_y(), Rueckgabewert vector der Loesung der DGL const vector<double>& get_zeit() const { return Zeit; } // Definition der konstanten Member-Funktion get_zeit(), Rueckgabewert vector der zeit-Punkte }; // Ende der Klasse double dsolve::f(double t, double y){ // Definition der Funktion f(t,y), Gleichung der DGL dy/dt=f(t,y) double wert; wert = y - pow(t,2) + 1; // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(t,y) } // Ende der Funktion f(t,y) double dsolve::y_analytisch(double t, double alpha){ // Analytische Loesung der DGL double wert; wert = (alpha + (pow(t,2) + 2*t + 1)*exp(-t) -1)*exp(t); // Eigentliche Definition der analytische Loesung return wert; // Rueckgabewert } // Ende der Definitiom int main(){ // Hauptfunktion dsolve Loes1 {0,4,500,0.3}; // Benutzt Konstruktor mit a=0, b=4, N=30 und alpha=0.5 vector<double> Zeit = Loes1.get_zeit(); // Aufrufen der Member-Funktion get_zeit() und kopieren der Zeitwerte vector<double> y_RungeK_4 = Loes1.get_y(); // Aufrufen der Member-Funktion get_y() und kopieren der Loesungswerte printf("# 0: Index i \n# 1: t-Wert \n# 2:Runge-Kutta Ordnung vier \n"); // Beschreibung der ausgegebenen Groessen printf("# 3: Analytische Loesung \n# 4: Fehler \n"); // Beschreibung der ausgegebenen Groessen for(int i=0; i < Zeit.size(); ++i){ // for-Schleife zur Terminalausgabe der Loesung printf("%3d %19.15f %19.15f %19.15f %19.15e \n",i, Zeit[i], y_RungeK_4[i], Loes1.y_analytisch(Zeit[i], 0.3), y_RungeK_4[i] - Loes1.y_analytisch(Zeit[i], 0.3)); } } // Ende der Hauptfunktion
Die Daten-Member der Klasse bestehen aus vielen, zuvor in der main()-Funktion definierten Variablen. Mittels des Konstruktors werden diese initialisiert und außerdem werden die, als private Daten-Member deklarierten Standardvektoren 'vector<double> y_RungeK_4' und 'vector<double> Zeit' im Anweisungsblock des Konstruktors mit den Lösungswerten gefüllt.
Das folgende Programm stellt hingegen eine Umformulierung mittels einer dsolve(...)-Funktion dar.
// Musterlösung der Aufgabe 1b des Übungsblattes Nr.9 /* Berechnung der Lösung einer Differentialgleichung der Form y'=f(t,y) * mittels Runge-Kutta Ordnung vier Verfahren * Verfahren zur Loesung der DGL ist in eine Funktion dsolve(Zeitvektor,Anfangswert) ausgelagert * Zeitentwicklung der fuer unterschiedliche t-Werte in [a,b] */ #include <stdio.h> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <vector> // Vector-Container der Standardbibliothek using namespace std; // Benutze den Namensraum std vector<double> dsolve( vector<double> Zeit, double alpha){ // Definition der Funktion 'dsolve' vector<double> y_RungeK_4( Zeit.size() + 1 ); // Deklaration eines double Vektors zum speichern der Loesung double k1, k2, k3, k4; // Deklaration der vier Runge-Kutta Parameter double h = Zeit[1] - Zeit[0]; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) y_RungeK_4[0] = alpha; double f(double t, double y); // Deklaration der Funktion f(t,y) (Definition findet ausserhalb der Funktion statt) for (int i = 0; i < Zeit.size(); ++i){ // Bereichsbasierte for-Schleife ueber die einzelnen Punkte des t-Intervalls k1 = h*f(Zeit[i],y_RungeK_4[i]); // Runge-Kutta Parameter 1 k2 = h*f(Zeit[i]+h/2,y_RungeK_4[i] + k1/2); // Runge-Kutta Parameter 2 k3 = h*f(Zeit[i]+h/2,y_RungeK_4[i] + k2/2); // Runge-Kutta Parameter 3 k4 = h*f(Zeit[i]+h,y_RungeK_4[i] + k3); // Runge-Kutta Parameter 4 y_RungeK_4[i+1] = y_RungeK_4[i] + (k1 + 2*k2 + 2*k3 + k4)/6; // Zum y-Vektor den neuen Wert eintragen } // Ende for-Schleife ueber die einzelnen Punkte des t-Intervalls return y_RungeK_4; // Rueckgabewert vector der Loesung der DGL } // Ende der Funktion dsolve double f(double t, double y){ // Definition der Funktion f(t,y), Gleichung der DGL dy/dt=f(t,y) double wert; wert = y - pow(t,2) + 1; // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(t,y) } // Ende der Funktion f(t,y) double y_analytisch(double t, double alpha){ // Analytische Loesung der DGL double wert; wert = (alpha + (pow(t,2) + 2*t + 1)*exp(-t) -1)*exp(t); // Eigentliche Definition der analytische Loesung return wert; // Rueckgabewert } // Ende der Definitiom int main(){ // Hauptfunktion double a = 0; // Untergrenze des Zeit-Intervalls [a,b] in dem die Loesung berechnet werden soll double b = 4; // Obergrenze des Intervalls [a,b] int N = 500; // Anzahl der Punkte in die das t-Intervall aufgeteilt wird double h = (b - a)/N; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) double alpha = 0.3; // Anfangswert bei t=a: y(a)=alpha vector<double> Zeit(N+1); // Deklaration des double-vector-Containers mit N+1 Einträgen (Gitterpunkte des Zeitintervalls) for(int i = 0; i < Zeit.size(); ++i){ // for-Schleife zum Festlegen der einzelnen Elemente des Zeitvektors Zeit[i] = a + i*h; // Wert-Zuweisung an das i-te Elementes des Zeitvektors } // Ende for-Schleife vector<double> y_RungeK_4 = dsolve(Zeit,alpha); // Definition des Loesungsvektors und Aufruf der Funktion dsolve(...) printf("# 0: Index i \n# 1: t-Wert \n# 2:Runge-Kutta Ordnung vier \n"); // Beschreibung der ausgegebenen Groessen printf("# 3: Analytische Loesung \n# 4: Fehler \n"); // Beschreibung der ausgegebenen Groessen for(int i = 0; i < Zeit.size(); ++i){ // for-Schleife zur Terminalausgabe der Loesung printf("%3d %19.15f %19.15f %19.15f %19.15e \n",i, Zeit[i], y_RungeK_4[i], y_analytisch(Zeit[i], 0.3), y_RungeK_4[i] - y_analytisch(Zeit[i], 0.3)); } } // Ende der Hauptfunktion
Der Rückgabewert der Funktion ist vom Typ double-Standardvektor ( vector<double> dsolve(vector<double> Zeit, double alpha){ ... } ) und die in diesem Container gespeicherten Gleitkommazahlen stellen die Elemente des Lösungsvektor $y_i$ der 'Runge-Kutta Ordnung vier'-Methode dar. Die Argumentenliste der Funktion enthält als ersten Eintrag den double-Standardvektor 'Zeit' ( vector<double> Zeit ) der Zeitgitterpunkte und das zweite Argument ist der Parameter $\alpha$ des Anfangswertes von y ($y(a)=y(0)=\alpha$).
Beide Varianten (Klassenstruktur und Funktion) haben leider das Manko, dass sie die DGL bestimmende Funktion $f(t,y(t)) = y - t^2 + 1$ als eine separate Funktion definieren, und falls der Benutzer die Form der DGL verändern möchte, muss er diese Funktion zunächst explizit umschreiben. Am Ende dieser Musterlösung wird eine weitere Funktionenversion eines C++ Programms vorgestellt, in der die DGL bestimmende Funktion $f(t,y(t))$ direkt vom Benutzer als Argument übergeben werden kann.
Führt man eines der beiden Programme aus, so erhält man die folgende Terminalausgabe, wenn man $N=50$ Zeit-Gitterpunkte $t_i, i=0,1,2, ..., N-1$ benutzt.
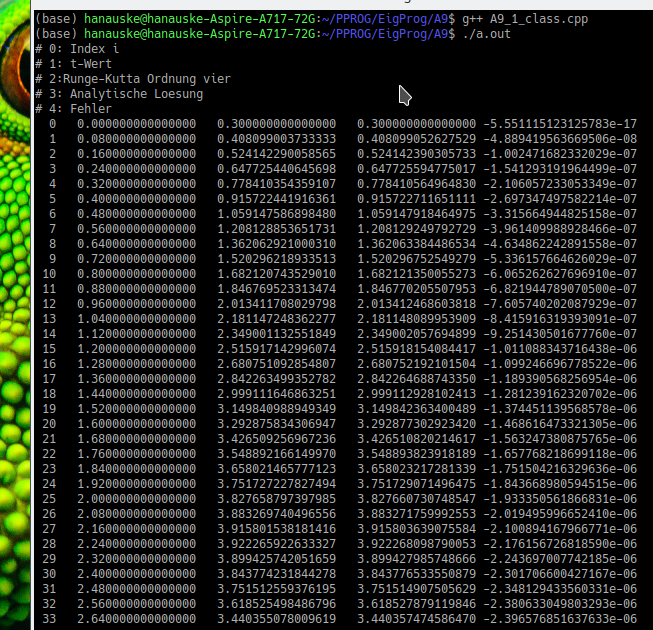
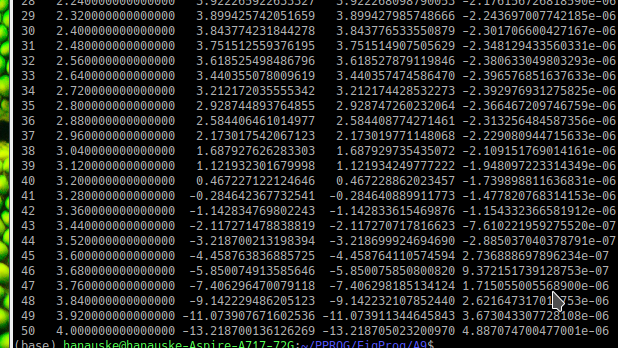
Für $N=500$ erhält man die folgenden Werte



, und für $N=5000$ ergibt sich die folgende Terminalausgabe:



Man erkennt deutlich, dass die approximierten Werte des Lösungsvektors $y_i$ sich bei ansteigender Anzahl der Zeit-Gitterpunkte $N$ dem wirklichen Wert der analytischen Lösung immer stärker annähern. Außerdem ist ein generelles Ansteigen des Fehlers ${\cal F} = y_i - y_{analytisch}(t_i)$ im Laufe der Zeit zu beobachten. Für $t=1$ und $N=50$ ($N=5000$) erhält man beispielsweise einen Fehler ${\cal F} \approx -8.4 \cdot 10^{-7}$ (${\cal F} = \approx -8.4 \cdot 10^{-15} $), wohingegen man am Ende der Simulation bei $t=4$ den Fehler ${\cal F} \approx 4.9 \cdot 10^{-6}$ (${\cal F} = \approx 1.6 \cdot 10^{-13}$) erhält.
Das folgende C++ Programm stellt eine vortgeschrittene Version des 'Runge-Kutta-Solvers' dar, bei der der Kern-Algorithmus in eine Template-Funktion 'runge_kutta(...)' ausgelagert wurde. Das Programm wurde von Alexander Gehwald und Johannes Misch erstellt. Der Vorteil des Programmes besteht unter anderem darin, dass der Benutzer, falls er die numerische Lösung einer eine andere DGL berechnen möchte, dies einfach beim Aufruf der Funktion spezifizieren kann. Zusätzlich wurde die gesamte Funktion in eine separate Datei (runge_kutta.hpp) ausgelagert und das Namespace 'namespace detail' definiert (Templates und Namespaces werden erst in einer späteren Vorlesung genauer behandelt). Der Quelltext der Hauptfunktion befindet sich in einer zweiten Datei (main.cpp) und in ihm wird die Datei runge_kutta.hpp mittels des Befehls '#include "runge_kutta.hpp"' eingebunden. Beim Aufrufen der Funktion runge_kutta(...) aus dem Hauptprogramm spezifiziert der Anwender die DGL (die Funktion $f(t,y(t))$), die Anfangswerte, $h$ und den Zeitendpunkt. Die folgenden Abbildungen zeigen das Programm main.cpp und die Datei runge_kutta.hpp der Version von Alexander Gehwald und Johannes Misch. Leider kann man das ausführbare Programm nicht mit alten C++ Kompilern erstellen, sondern man muss mindestens Version C++17 verwenden (kompiliere mit 'g++ -std=c++17 main.cpp').
/** Berechnung der Lösung einer Differentialgleichung der Form y'=f(t,y) * mittels Runge-Kutta Ordnung vier Verfahren. * Das Verfahren zur Loesung der DGL wurde in eine Funktion runge_kutta(...), * in einer externen Datei 'runge_kutta.hpp' ausgelagert, die * mittels #include "runge_kutta.hpp" eingebunden wird. * Zeitentwicklung der fuer unterschiedliche t-Werte in [a,b] * Diese Version des C++ Programm wurde von * Johannes Misch ( misch@itp.uni-frankfurt.de ) und Alexander Gehwald ( gehwald@itp.uni-frankfurt.de ) erstellt * Zum Kompilieren des Programms bitte das Folgende eingeben: g++ -std=c++17 main.cpp **/ #include "runge_kutta.hpp" #include <cmath> #include <iostream> int main() { constexpr int n{500}; constexpr double y_0{0.3}; constexpr double t_0{0.0}; constexpr double t_end{4.0}; constexpr double h{t_end / n}; constexpr auto f = [](const auto y, const auto t){ return ( y - pow(t,2) + 1); }; const auto res = musterloesung::runge_kutta<4>(f, {y_0, t_0}, h, t_end); for (const auto [y, t] : res) { std::cout << t << ' ' << y << '\n'; } return 0; }
/** Funktion zur Berechnung der Lösung einer Differentialgleichung der Form y'=f(t,y) * mittels Runge-Kutta Ordnung vier Verfahren. * Diese Version des C++ Programm wurde von * Johannes Misch ( misch@itp.uni-frankfurt.de ) und Alexander Gehwald ( gehwald@itp.uni-frankfurt.de ) erstellt * Zum Kompilieren bitte das Folgende eingeben: g++ -std=c++17 main.cpp **/ #pragma once #include <cmath> #include <cstddef> #include <type_traits> #include <utility> #include <vector> namespace musterloesung { namespace detail { template<typename T> struct RungeKuttaPoint { T y; double t; // This is needed before C++20, otherwise it can't be properly used in std::vector RungeKuttaPoint(T y_, const double t_) : y{std::move(y_)}, t{t_} { } }; template<typename T> using RungeKuttaResult = std::vector<RungeKuttaPoint<T>>; template<std::size_t order, typename T, typename Function> [[nodiscard]] auto rk_step(Function&& f, const RungeKuttaPoint<T> current, const double step_width) noexcept { static_assert(std::is_floating_point_v<T>, "T must be a floating point type."); const T k1 = f(current.y, current.t); if constexpr (order == 1) { return current.y + k1; } else if constexpr (order == 2) { const T k2 = f(current.y + 0.5 * k1, current.t + 0.5 * step_width); return current.y + step_width * k2; } else if constexpr (order == 3) { const T k2 = f(current.y + k1, current.t + step_width); const T k3 = f(current.y + (1.0 / 4.0) * (k1 + k2), current.t + 0.5 * step_width); return current.y + (step_width / 6.0) * (k1 + k2 + 4.0 * k3); } else if constexpr (order == 4) { const T k2 = f(current.y + step_width * 0.5 * k1, current.t + 0.5 * step_width); const T k3 = f(current.y + step_width * 0.5 * k2, current.t + 0.5 * step_width); const T k4 = f(current.y + step_width * k3, current.t + step_width); return current.y + (step_width / 6.0) * (k1 + 2.0 * k2 + 2.0 * k3 + k4); } else { static_assert(false and sizeof(T), "Implementation of higher orders is left to the inclined reader."); } } } template<std::size_t order, typename T = void, typename Function = void> [[nodiscard]] auto runge_kutta(Function&& f, const detail::RungeKuttaPoint<T> initial, const double step_width, const T t_end) noexcept { static_assert(std::is_invocable_r_v<decltype(initial.y / initial.t), Function, T, double>, "Please provide a suitable function."); static_assert(std::is_same_v<T, decltype(initial.y * 0.5)>, "T must be scalable by double."); const auto n_points = static_cast<std::size_t>((t_end - initial.t) / step_width); detail::RungeKuttaResult<T> res; res.reserve(n_points); auto [y, t] = initial; res.emplace_back(y, t); for (int i = 1; t < t_end; ++i) { y = detail::rk_step<order, T>(f, {y, t}, step_width); t = initial.t + i * step_width; res.emplace_back(y, t); } return res; } }
Musterlösung zur Aufgabe 2 (10 Punkte)
Das folgende Programm stellt eine Abänderung des C++ Programms Vector_Dinge.cpp dar. In der inline Funktion 'Gehe_Zeitschritt(...)' wurden einerseits periodische Randbedingungen anstelle der Reflexion an den Rändern der Kiste eingebaut, andererseits wurde eine zusätzlich Teilchen/Umgebungseigenschaft in die Funktion implementiert. Es handelt sich dabei um eine fiktive Box im unteren linken Bereich der Kiste, die die Eigenschaft besitzt, dass falls ein Teilchen in diesen Bereich gerät, es ruhend, entsprechend seiner Nummer auf der x-Achse positioniert wird.
// Musterlösung der Aufgabe 2 des Übungsblattes Nr.9 /* Ausgabe zum Plotten (Python) mittels: "./a.out > A9_2.dat" * python3 A9_2.py */ #include <iostream> // Ein- und Ausgabebibliothek #include <vector> // Sequenzieller Container vector<Type> der Standardbibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) using namespace std; // Benutze den Namensraum std //Definition der Klasse 'Ding' class Ding{ // Private Instanzvariablen (Daten-Member) der Klasse unsigned int n; // Nummer des Dinges double x = 0, y = 0, z = 0; // Ort des Dinges double v_x = 0, v_y = 0, v_z = 0; // Geschwindigkeit des Dinges // Oeffentliche Konstruktoren und Member-Funktionen der Klasse public: // Fuenf ueberladene Konstruktoren der Klasse // Konstruktor mit sieben Argumenten Ding(unsigned int set_n, double set_x, double set_y, double set_z, double set_v_x, double set_v_y, double set_v_z) : n{set_n}, x{set_x}, y{set_y}, z{set_z}, v_x{set_v_x}, v_y{set_v_y}, v_z{set_v_z} { printf("# Konstruktor(n,x,y,z,,vx,vy,vz) erzeugt das Ding %i \n",n); } // Konstruktor mit vier Argumenten Ding(unsigned int set_n, double set_x, double set_y, double set_z) : n{set_n}, x{set_x}, y{set_y}, z{set_z} { printf("# Konstruktor(n,x,y,z) erzeugt ein das Ding %i \n",n); } // Konstruktor mit drei Argumenten Ding(unsigned int set_n, double set_x, double set_y) : n{set_n}, x{set_x}, y{set_y} { printf("# Konstruktor(n,x,y) erzeugt das Ding %i \n",n); } // Konstruktor mit zwei Argumenten Ding(unsigned int set_n, double set_x) : n{set_n}, x{set_x} { printf("# Konstruktor(n,x) erzeugt das Ding %i \n",n); } // Konstruktor ohne Argument (Standard-Konstruktor) Ding() : n{0} { printf("# Konstruktor() erzeugt das Ding %i \n", n); } // Member-Funktionen der Klasse void Gehe_Zeitschritt(double dt, double max_x, double max_y, double max_z); // Deklaration einer Member-Funktion (Definition findet ausserhalb der Klasse statt) // als const deklariert, da sie die privaten Instanzvariablen nicht veraendern: unsigned int get_Nummer() const {return n;} double get_Ort_x() const {return x;} double get_Ort_y() const {return y;} double get_Ort_z() const {return z;} double get_Geschw_x() const {return v_x;} double get_Geschw_y() const {return v_y;} double get_Geschw_z() const {return v_z;} }; /* Definition der Funktion Gehe_Zeitschritt(...) als inline-Methode der Klasse Ding * Die Funktion beschreibt die Veränderung der Ortskoordinaten (x,y,z) bei einem Zeitschritt dt * Es sind zusaetzlich spezielle Randbedingungen an die Bewegung formuliert, so dass sich die * Dinge nur in einem Bereich von [0,max_x], [0,max_y] und [0,max_z] bewegen koennen */ inline void Ding::Gehe_Zeitschritt(double dt, double max_x, double max_y, double max_z){ x = x + v_x * dt; y = y + v_y * dt; z = z + v_z * dt; // Periodische Randbedingungen an die Kiste if (x < 0){x = max_x;} if (x > max_x){x = 0;} if (y < 0){y = max_y;} if (y > max_y){y = 0;} if (z < 0){z = max_z;} if (z > max_z){z = 0;} // Falls das Ding in die untere linke Ecke kommt, wird es // auf der Horizontalen bei y=0 entsprechend seiner Nummer angeordnet if (x < 5 && y < 5){ v_x = 0; v_y = 0; v_z = 0; x = max_x*n/70; y = 0; z = 0; } } int main(){ // Hauptfunktion double kiste_x = 40; // Laenge der Kiste double kiste_y = 40; // Breite der Kiste unsigned int Anz_Teilchen = 70; // Definition der Anzahl der zu erzeugenden Dinge double t; // Deklaration des Zeitparameters double dt = 0.2; // Definition der Laenge des Zeitschrittes double Anz_tSchritte = 300; // Anzahl der Zeitschritte vector<Ding> Kiste_Teilchen; // Deklaration eines vector-Containers for (unsigned int n = 0; n < Anz_Teilchen; ++n){ // for-Schleife zum Auffuellen des Containers mit Elementen vom Typ 'Ding' // Initialisierung diaginal in der x-y-Ebene, Geschwindigkeit in x- und y-Richtung Kiste_Teilchen.push_back( Ding {n, n*kiste_x/Anz_Teilchen + 0.1, n*kiste_x/Anz_Teilchen + 0.1, 0, sin(n+1.0), cos(n+1.0), 0} ); } printf("# 0: Index i \n# 1: Zeit t \n# 2: Nummer des Teilchens 1 \n"); // Beschreibung der ausgegebenen Groessen printf("# 3: x-Position des Teilchens 1 \n# 4: y-Position des Teilchens 1 \n"); // Beschreibung der ausgegebenen Groessen printf("# 5: Nummer des Teilchens 2 \n# 6: .... bis Anzahl der Teichen \n"); // Beschreibung der ausgegebenen Groessen for (int i = 0; i < Anz_tSchritte; ++i){ // for-Schleife fuer die zeitliche Entwicklung der Dinge in der Kiste t = i * dt; // Zeit geht in dt-Schritten voran printf("%3i %10.6f ", i, t); // Ausgabe Index i und Zeit t for (auto& n : Kiste_Teilchen){ // Bereichsbasierte for-Schleife zum Ausgeben der x-y-Orte der Dinge printf("%3i %10.6f %10.6f ", n.get_Nummer(), n.get_Ort_x(), n.get_Ort_y()); // Ausgabe Teilchenorte n.Gehe_Zeitschritt(dt,kiste_x, kiste_y, 0.0); // Aufruf der inline Funktion Gehe_Zeitschritt(...) } printf("\n"); } }
Mittels des Konstruktors wurden 70 Objekte der Klasse Ding mit unterschiedlichen Anfangsorten und Geschwindigkeiten erstellt. Einige der Teilchen mit niedriger Nummer $n$ sind bereits bei der Initialisierung im unteren Bereich der Kiste, sodass sie gleich beim ersten Zeitschritt auf der x-Achse ruhend positioniert werden. Das folgende Python-Skript visualisiert dann die vom C++ Programm berechneten Teilchenbewegungen:
# Python Plot zur Musterlösung der Aufgabe 2 des Übungsblattes Nr.9 # Python Programm zum Plotten der Daten des Vector-Containers mit 70 Dingen (A9_2.cpp) # Es werden hier mehrere Bilder der zeitlichen Entwicklung des Systems in einem Ordner 'Bilder' gespeichert # !!!! Sie muessen vor der Ausfuehrung des Programms den Ordner Bilder erstellen !!!! # Die einzelnen Bilder kann mann dann mittels des folgenden Terminalbefehls zu einem Video binden: # ffmpeg -framerate 5 -i './Vector_Dinge_%03d.png' -c:v libx264 A9_2.mp4 import matplotlib.pyplot as plt # Python Bibliothek zum Plotten (siehe https://matplotlib.org/ ) import matplotlib.patches as patches import numpy as np # Python Bibliothek fuer Mathematisches (siehe https://numpy.org/ ) data = np.genfromtxt("./A9_2.dat") # Einlesen der berechneten Daten von A9_2.cpp fig, ax = plt.subplots() ax.set_title(r'Container mit Teilchen') # Titel der Abbildung ax.set_ylabel('y') # Beschriftung y-Achse ax.set_xlabel('x') # Beschriftung x-Achse r = 200 # Radius eines Dings plot_min=0 # Festlegung der x-Untergrenze (Abmessung Kiste) plot_max=40 # Festlegung der x-Obergrenze (Abmessung Kiste) anz_teilchen = int(len(data[0,:])/3) # Definition der Anzahl der Dinge cmap = plt.cm.nipy_spectral # Definition der Farbschattierung der Dinge line_colors = cmap (np.linspace(0.2,1,anz_teilchen)) # Definition der Farbschattierung der Dinge alp = 0.9 # Transparenz eines Dinges Box = patches.Rectangle((0, 0), 40, 40, linewidth=3, edgecolor='grey', facecolor='none') Box_klein = patches.Rectangle((0, 0), 5, 5, linewidth=1, edgecolor='red', facecolor='grey', alpha=0.6) for it in range(len(data[:,0])): # for-Schleife fuer die zeitliche Entwicklung der Dinge in der Kiste print(it) # Terminalausgabe der Erstellung des i-ten Bildes ax.cla() ax.add_patch(Box) ax.add_patch(Box_klein) for i in range(anz_teilchen): # for-Schleife ueber die Teilchen in der Kiste ax.scatter(data[it,3*i+3],data[it,3*i+4], marker='o', color=line_colors[i], s=r) # Kennzeichnung der Position des Dinges durch einen blauen Kreis ax.text(data[it,3*i+3],data[it,3*i+4], str(int(data[it,3*i+2])), fontsize=10, verticalalignment='center', horizontalalignment='center', color="white", alpha=alp) # Ding Nr. ax.set_xlim(plot_min-1,plot_max+1) # Plot-Limit x-Achse ax.set_ylim(plot_min-1,plot_max+1) # Plot-Limit y-Achse # Bild-Ausgabe mit Speicherung eines individuellen Iteration-Namens pic_name = "./Bilder/" + "Vector_Dinge_" + "{:0>3d}".format(it) + ".png" plt.savefig(pic_name, dpi=200,bbox_inches="tight",pad_inches=0.05,format="png")
Die unten abgebildete Animation zeigt die Bewegung der 70 Teilchen und wurde mittels des oberen Python-Skriptes erstellt. Im Laufe der Simulation (die aus 300 Einzelbildern besteht) gelangen weitere Teichen in den unteren linken Bereich, und auch sie werden dann bei $y=0$ positioniert.