Musterlösung zum Übungsblatt Nr. 8
Musterlösung zur Aufgabe 1 (10 Punkte)
Das folgende C++ Programm beinhaltet die Klasse 'class Integral' und die inline-Methode 'inline double Integral::f(double x){ ... }'. In der 'int main(){ ...}' Funktion werden vier Integral-Objekte mittels unterschiedlicher Konstruktoren erzeugt, wobei diese Integral-Instanzen sich in der Anzahl der Teilintervalle $ts$ unterscheiden.
// Musterlösung der Aufgabe 1 des Übungsblattes Nr.8 /* Die Klasse Integral berechnet das bestimmte Integral * einer Funktion f(x) in den Grenzen [a,b] * mittels einer stückweise numerischen Integration (ts Teilintervalle) * und benutzt in jedem der Teilintervalle die N=4 Integrationsregel */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) //Definition der Klasse 'Integral' class Integral{ // Private Instanzvariablen (Daten-Member) der Klasse double a; // Untergrenze des bestimmten Integrals double b; // Obergrenze des bestimmten Integrals unsigned ts; // Anzahl der Teilintervalle (wurde zuvor mit der Variable ts bezeichnet) // Oeffentliche Konstruktoren und Member-Funktionen der Klasse public: // Drei ueberladene Konstruktoren der Klasse Integral(double set_a, double set_b, unsigned int set_ts) : a{set_a}, b{set_b}, ts{set_ts} { } Integral(double set_a, double set_b) : a{set_a}, b{set_b}, ts{10} { } Integral() : a{0}, b{1}, ts{10} { } // Member-Funktionen der Klasse double f(double x); // Deklaration der Member-Funktion f(x) (Definition findet ausserhalb der Klasse statt) double integrate() { // Member-Funktion der Klasse zur Berechnung des bestimmten Integrals double I_wert = 0; // Variable fuer den zu berechnenden Integralwert double h = (b-a)/(4*ts); // Deklaration des h-Wertes fuer die N=4 Integrationsregel double x_u; // x-Untergrenze der Teilintegration for(int i = 0; i < ts; ++i){ // Schleifen Anfang ueber die einzelnen Teilintegrationen x_u = a + 4*i*h; // Setzen der neuen x-Untergrenze der nächsten Teilintegration I_wert = I_wert + 2*h/45*(7*f(x_u) + 32*f(x_u+h) + 12*f(x_u+2*h) + 32*f(x_u+3*h) + 7*f(x_u+4*h)); // N=4 Regel } // Ende for-Schleife return I_wert; // Rueckgabe des berechnenden Integralwertes } // Ende der Member-Funktion integrate() }; inline double Integral::f(double x){ // Definition der Funktion f(x) als inline-Methode der Klasse Integral double wert; wert = 10 * exp(-x/5) * sin(3*x); // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } int main(){ // Hauptfunktion double I_analyt = - 4.7587485166819485; // Analytischer Wert des Integrals, mittels Jupyter-Sympy berechnet (Grenzen [a,b]=[1,2]) Integral I1 {1,2}; // Benutzt Integral(a,b) mit ts=10 Integral I2 {1,2,50}; // Benutzt Integral(a,b,ts) mit ts=50 Integral I3 {1,2,100}; // Benutzt Integral(a,b,ts) mit ts=100 Integral I4 {1,2,1000000}; // Benutzt Integral(a,b,ts) mit ts=100000 // Terminalausgabe printf("I1 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 10) \n", I1.integrate(), I1.integrate() - I_analyt); printf("I2 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 50) \n", I2.integrate(), I2.integrate() - I_analyt); printf("I3 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 100) \n", I3.integrate(), I3.integrate() - I_analyt); printf("I4 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 1 Millionen) \n", I4.integrate(), I4.integrate() - I_analyt); printf("Analytisch I = %20.14f\n", I_analyt); }
Führt man das Programm A8_1.cpp aus, so erhält man die folgende Terminalausgabe (siehe erste, obere Ausgabe):
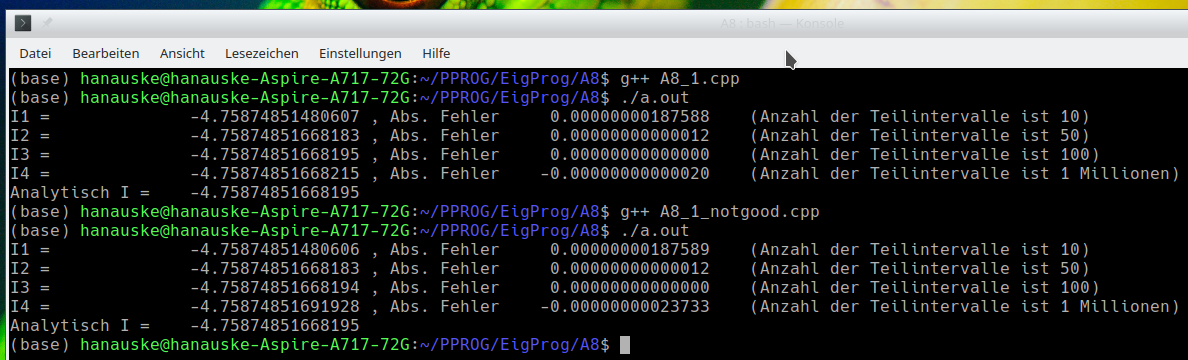
Man erkennt, dass der absolute Fehler in der approximativen Berechnung des Integralwertes , zunächst, mit steigender Anzahl der Teilintervalle (steigendem Wert von $ts$) kleiner wird. Bei $ts=100$ ist der berechnete Wert auf 14 Nachkommastellen genau! Erhöht man die Anzahl der Teilintervalle jedoch immer weiter, so steigt der Fehler bei der Berechnung, bei sehr hohen Werten von $ts$, jedoch wieder an. Bei $ts=1000000$ ist der berechnete Wert nur noch auf 12 Nachkommastellen genau! Der Grund hierfür liegt in einer kumulativen Erzeugung von Rundungsfehlern innerhalb der for-Schleife der Klasse. Der Programmierer ist somit in der Exaktheit seiner numerischen Berechnungen beschränkt. Das Gewicht solcher Rundungsfehler kann sich bei einer unvorteilhaften Inkrementierung von Gleitkommazahlen erhöhen.
In dem unteren C++ Programm wurde z.B. die Art und Weise, wie sich die Teiluntergrenze $x_u$ innerhalb der for-Schleife erhöht verändert. Führt man das Programm A8_1_notgood.cpp aus, so erhält man die oben dargestellt Terminalausgabe (siehe zweite, untere Ausgabe). Bei $ts=1000000$ ist der berechnete Wert nur noch auf 9 Nachkommastellen genau, da durch die Anweisung 'x_u = x_u + 4*h;' in jedem neuen Teilintervall der Rundungsfehler, von den zuvor berechneten, mit aufaddiert wird.
// Musterlösung der Aufgabe 1 des Übungsblattes Nr.8 /* Die Klasse Integral berechnet das bestimmte Integral * einer Funktion f(x) in den Grenzen [a,b] * mittels einer stückweise numerischen Integration (ts Teilintervalle) * und benutzt in jedem der Teilintervalle die N=4 Integrationsregel * In dieser Version wurde eine unvorteilhafte Implementierung der Erhoehung von x_u benutzt */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) //Definition der Klasse 'Integral' class Integral{ // Private Instanzvariablen (Daten-Member) der Klasse double a; // Untergrenze des bestimmten Integrals double b; // Obergrenze des bestimmten Integrals unsigned ts; // Anzahl der Teilintervalle (wurde zuvor mit der Variable ts bezeichnet) // Oeffentliche Konstruktoren und Member-Funktionen der Klasse public: // Drei ueberladene Konstruktoren der Klasse Integral(double set_a, double set_b, unsigned int set_ts) : a{set_a}, b{set_b}, ts{set_ts} { } Integral(double set_a, double set_b) : a{set_a}, b{set_b}, ts{10} { } Integral() : a{0}, b{1}, ts{10} { } // Member-Funktionen der Klasse double f(double x); // Deklaration der Member-Funktion f(x) (Definition findet ausserhalb der Klasse statt) double integrate() { // Member-Funktion der Klasse zur Berechnung des bestimmten Integrals double I_wert = 0; // Variable fuer den zu berechnenden Integralwert double h = (b-a)/(4*ts); // Deklaration des h-Wertes fuer die N=4 Integrationsregel double x_u=a - 4*h; // x-Untergrenze der Teilintegration for(int i = 0; i < ts; ++i){ // Schleifen Anfang ueber die einzelnen Teilintegrationen x_u = x_u + 4*h; // Setzen der neuen x-Untergrenze der nächsten Teilintegration: nicht gut!, besser : // x_u = a + 4*i*h; // Hierdurch werden die immer auftretenden Rundungsfehler kleiner, da nur einmal addiert wird I_wert = I_wert + 2*h/45*(7*f(x_u) + 32*f(x_u+h) + 12*f(x_u+2*h) + 32*f(x_u+3*h) + 7*f(x_u+4*h)); // N=4 Regel } // Ende for-Schleife return I_wert; // Rueckgabe des berechnenden Integralwertes } // Ende der Member-Funktion integrate() }; inline double Integral::f(double x){ // Definition der Funktion f(x) als inline-Methode der Klasse Integral double wert; wert = 10 * exp(-x/5) * sin(3*x); // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } int main(){ // Hauptfunktion double I_analyt = - 4.7587485166819485; // Analytischer Wert des Integrals, mittels Jupyter-Sympy berechnet (Grenzen [a,b]=[1,2]) Integral I1 {1,2}; // Benutzt Integral(a,b) mit ts=10 Integral I2 {1,2,50}; // Benutzt Integral(a,b,ts) mit ts=50 Integral I3 {1,2,100}; // Benutzt Integral(a,b,ts) mit ts=100 Integral I4 {1,2,1000000}; // Benutzt Integral(a,b,ts) mit ts=100000 // Terminalausgabe printf("I1 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 10) \n", I1.integrate(), I1.integrate() - I_analyt); printf("I2 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 50) \n", I2.integrate(), I2.integrate() - I_analyt); printf("I3 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 100) \n", I3.integrate(), I3.integrate() - I_analyt); printf("I4 = %20.14f , Abs. Fehler %20.14f (Anzahl der Teilintervalle ist 1 Millionen) \n", I4.integrate(), I4.integrate() - I_analyt); printf("Analytisch I = %20.14f\n", I_analyt); }
Den Algorithmus der Integration hätte man wohl besser in einer normalen C++ Funktion implementiert, da das Deklarieren der Integral-Instanzen und die erst danach folgende Integralberechnung ein wenig umständlich ist.
Musterlösung zur Aufgabe 2 (10 Punkte)
Die folgend Musterlösung basiert auf dem Programm Lagrange_Polynom_Klasse_a.cpp.
// Musterlösung der Aufgabe 2 des Übungsblattes Nr.8 /* Entwicklung einer Funktion in ein Lagrange Polynom (mit ausgelagerter 'LagrangePoly'-Klasse) * Bei vorgegebenen (N+1) x-y-Stuetzstellenpunkten berechnet man ein Lagrange Polynom vom Grade N. * Hier speziell 8 Punkte * Ausgabe zum Plotten (Python-Skript PythonPlot_A8_2.py) mittels: "./a.out > A8_2.dat" */ #include <iostream> // Ein- und Ausgabebibliothek //Definition der Klasse 'LagrangePoly' class LagrangePoly { // Private Instanzvariablen (Daten-Member) der Klasse double* points_x; // Zeigervariable der x-Werte der Stuetzstellenpunkte double* points_y; // Zeigervariable der y-Werte der Stuetzstellenpunkte unsigned int N_points; // Anzahl der Stuetzstellenpunkte // Oeffentliche Konstruktoren und Member-Funktionen der Klasse public: // Konstruktor mit drei Argumenten LagrangePoly(double* set_points_x, double* set_points_y, unsigned int set_N_points) : points_x{set_points_x}, points_y{set_points_y}, N_points{set_N_points} {} double rechne(double x) { // Member-Funktion der Klasse zur Berechnung des approximierten Polynomwertes double Pfp = 0; // Deklaration und Initialisierung des Funktionswertes des approximierten Polynoms double Lk = 0; // Deklaration und Initialisierungeiner Zusatzvariable for(int k = 0; k < N_points; ++k){ // For-Schleife der Summation in der Lagrange Polynom Methode Lk=1; // Initialisierung der Produktvariable Lk mit 1 for(int i = 0; i < N_points; ++i){ // For-Schleife der Produktbildung in der Lagrange Polynom Methode if(i != k){ // Die Produktbildung soll nur fuer (i ungleich k) erfolgen Lk = Lk * (x - points_x[i])/(points_x[k] - points_x[i]); // Berechnung der Lk-Werte in der Lagrange Polynom Methode } // Ende if-Bedingung } // Ende for-Schleife der Produktbildung Pfp = Pfp + points_y[k]*Lk; // Kern-Gleichung in der Lagrange Polynom Methode } // Ende for-Schleife der Summenbildung return Pfp; // Rueckgabe des berechneten, approximierten Polynomwertes } // Ende der Member-Funktion rechne(double x) }; // Ende der Klassendefinition int main(){ // Hauptfunktion double points_x[] = { 1.1, 10.1, 12.9, 25.7, 40.5, 60.2, 95.1, 98.8 }; // Deklaration und Initialisierung der x-Werte der Stützstellen als double-Array double points_y[] = { 2.1, 41.5, 48.2, 35.2, 5.2 , 10.6, 27.5, 15.2 }; // Deklaration und Initialisierung der y-Werte der Stützstellen als double-Array unsigned int N_points = sizeof(points_x)/sizeof(points_x[0]); // Anzahl der Punkte die zur Approximation verwendet werden double plot_a = 0; // Untergrenze des x-Intervalls in dem die Ergebnisse ausgegeben werden sollen double plot_b = 100; // Obergrenze des x-Intervalls in dem die Ergebnisse ausgegeben werden sollen const unsigned int N_xp = 500; // Anzahl der Punkte in die das x-Intervall aufgeteilt wird double dx = (plot_b - plot_a)/N_xp; // Abstand dx zwischen den aequidistanten Punkten des x-Intervalls double x = plot_a-dx; // Aktueller x-Wert double xp[N_xp+1]; // Deklaration der x-Ausgabe-Punkte als double-Array double Pfp[N_xp+1]; // Deklaration der Ausgabe-Punkte des Polynoms als double-Array LagrangePoly Poly1 {points_x, points_y, N_points}; // Aufruf des Konstruktors der Klasse LagrangePoly (Erzeugung des Objektes 'Poly1') printf("# x-Werte der %3d Stuetzstellen-Punkte: \n", N_points); // Beschreibung der ausgegebenen Groessen for(int k = 0; k < N_points; ++k){ // For-Schleife der Ausgabe der Stuetzstellen x-Werte printf("%10.5f",points_x[k]); // Ausgabe der Stuetzpunkte } // Ende for-Schleife der Ausgabe printf("\n"); // Zeilenumbruch printf("# y-Werte der %3d Stuetzstellen-Punkte: \n", N_points); // Beschreibung der ausgegebenen Groessen for(int k = 0; k < N_points; ++k){ // For-Schleife der Ausgabe der Stuetzstellen y-Werte printf("%10.5f",points_y[k]); // Ausgabe der Stuetzpunkte } // Ende for-Schleife der Ausgabe printf("\n"); // Zeilenumbruch printf("# 0: Index j \n# 1: x-Wert \n"); // Beschreibung der ausgegebenen Groessen printf("# 2: Funktionswert des Lagrange Polynoms P(x) \n"); // Beschreibung der ausgegebenen Groessen for(int j = 0; j <= N_xp; ++j){ // For-Schleife die ueber die einzelnen Punkte des x-Intervalls geht x = j*dx; // Aktueller x-Wert xp[j] = x; // Eintrag des aktuellen x-Wertes in das x-Array Pfp[j] = Poly1.rechne(x); // Eintrag des aktuellen approximierten Polynom-Wertes in das Pfp-Array (Aufruf der Member-Funktion rechne(x)) } // Ende der for-Schleife ueber die einzelnen Punkte des x-Intervalls for(int j = 0; j <= N_xp; ++j){ // For-Schleife der separaten Ausgabe der berechneten Werte printf("%3d %14.10f %14.10f \n",j, xp[j], Pfp[j]); // Ausgabe der berechneten Werte } // Ende for-Schleife der Ausgabe } // Ende der Hauptfunktion
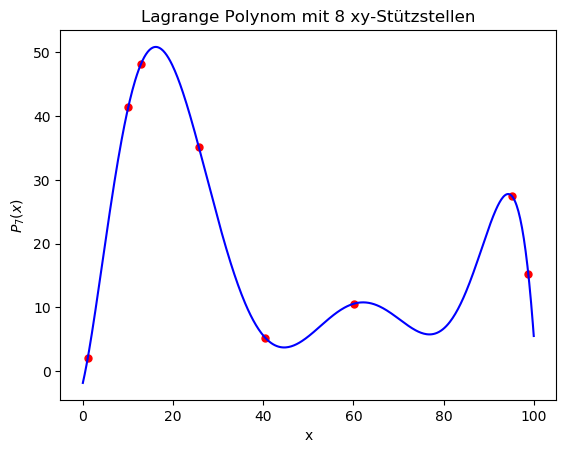
Innerhalb der Klasse wurde die zusätzliche Zeigervariable 'double* points_y;' als Daten-Member der Klasse deklariert, sodass auch die y-Werte der Stützstellenpunkte ($\vec{y} = \left( 2.1, 41.5, 48.2, 35.2, 5.2 , 10.6, 27.5, 15.2 \right)$) als eine zentrale Klasseneigenschaft auftreten. Mittels des neuen Konstruktors (jetzt drei Einträge in der Argumentenliste) kann der Benutzer nun sowohl die x- als auch y-Werte der Stützstellen initialisieren. Die zuvor, im Programm Lagrange_Polynom_Klasse_a.cpp benutzte inline-Funktion $f(x)$ wird nun nicht mehr benötigt. Das eigentliche Objekt der LagrangePoly-Klasse wird mittels der Anweisung 'LagrangePoly Poly1 {points_x, points_y, N_points};' im Hauptprogramm erzeugt. Im ersten Teil des Hauptprogramms werden unter anderem die x- und y-Werte der Stützstellenpunkte als zwei eindimensionale double-Arrays deklariert und mit den entsprechenden Werten der Aufgabenstellung initialisiert ($\vec{x} = \left( 1.1, 10.1, 12.9, 25.7, 40.5, 60.2, 95.1, 98.8 \right)$ und $\vec{y} = \left( 2.1, 41.5, 48.2, 35.2, 5.2 , 10.6, 27.5, 15.2 \right)$). Die Berechnung des Lagrange Polynoms $P_7(x)$ für $500$ äquidistant im Teilintervall $[a,b]=[0,100]$ aufgeteilte x-Werte wird mittels der Member-Funktion 'Poly1.rechne(x)' gemacht und der so approximierte Polynomwert wird in dem Array 'Pfp[j]' gespeichert (Pfp[j] = Poly1.rechne(x);). Zuletzt erfolgt dann, in einer getrennten for-Schleife, die Terminalausgabe der berechneten Polynomwerte. Die nebenstehende Abbildung zeigt die Visualisierung der vom C++ Programm A8_2.cpp ausgegebenen Daten, wobei die Grafik mittels des unten abgebildeten Python Skriptes PythonPlot_A8_2.py gemacht wurde.
Die Verwendung einer Klassenstruktur, für die Berechnung eines mittels der Stützstellenvektoren $\vec{x}$ und $\vec{y}$ definierten Lagrange Polynoms, ist sicherlich begründbar, da das Objekt durch seine Member Daten vollständig definiert ist und die Member-Methode des Kern-Algorithmus der Methode eine Art von Verhalten des Objektes darstellt. Dieses "Verhalten" wird durch den Aufruf der Member Funktion 'Poly1.rechne(x)' eingeleitet und der Rückgabewert entspricht einer Art von Antwort des Objektes. So in etwa als ob der Benutzer fragt: "Welchen $y$-Wert haben Sie an der Stelle $x$ ?" und das Objekt antwortet: "Mein $y$-Wert beträgt $...$ ?". Für den Benutzer wäre jedoch wohl auch hier eine Implementierung des Kern-Algorithmus innerhalb einer normalen C++ Funktion einfacher anzuwenden.
# Python Programm zum Plotten (x-y)-Wertetabelle (A8_2.cpp) import matplotlib.pyplot as plt # Python Bibliothek zum Plotten (siehe https://matplotlib.org/ ) import numpy as np # Python Bibliothek fuer Mathematisches (siehe https://numpy.org/ ) points_x = np.genfromtxt("./A8_2.dat", max_rows=1) # Einlesen x-Werte der Stuetzstellen points_y = np.genfromtxt("./A8_2.dat", skip_header=2, skip_footer=501) # Einlesen y-Werte der Stuetzstellen data = np.genfromtxt("./A8_2.dat", skip_header=4) # Einlesen xy-Werte der Polynoms plt.title(r'Lagrange Polynom mit 8 xy-Stützstellen') # Titel der Abbildung plt.ylabel(r'$P_7(x)$') # Beschriftung y-Achse plt.xlabel('x') # Beschriftung x-Achse plt.plot(data[:,1],data[:,2], color="blue") # Plotten des Polynoms plt.scatter(points_x,points_y, marker='o', color="red", s=25); # Plotten der Stuetzstellen plt.savefig("A8_2.png", bbox_inches="tight") # Speichern der Abbildung als Bild plt.show() # Zusaetzliches Darstellen der Abbildung im separaten Fenster