Musterlösung zum Übungsblatt Nr. 7
Musterlösung zur Aufgabe 1 (10 Punkte)
In dem Jupyter Notebook A7_1.ipynb (siehe A7_1.html) wird ein Teil einer Kurvendiskussion angefertigt. Gegeben sei die Funktion $f(x)$ $$ \begin{equation} f(x) = e^{-x^2/4} \cdot \hbox{sin}(x/10) \cdot \left( x^4 -q\,x^2 - 5 \right) \quad . \end{equation} $$
Nullstellensuche mit Jupyter und SympyBetrachten Sie sich die Funktion in ihrem gesamten Definitionsbereich ($x \in$ ℝ) und berechnen Sie für beliebige Parameter $q \in$ ℝ die Nullstellen der Funktion $f(x)=0$. Wie lauten die Nullstellenwerte für $q=9$ ?
Darstellung von $f(x)$, $f^\prime(x)$ und $f^{\prime\prime}(x)$ mittels JupyterStellen Sie nun die Funktion $f(x)$ und die erste und zweite Ableitung der Funktion im Teilintervall $x \in [-7,7]$ grafisch in drei x-y-Diagrammen dar (benutzen Sie dafür wieder den festen Parameterwert $q=9$). Versuchen Sie die Maxima der Funktion (mit $q=9$) mittels Sympy zu bestimmen.
Nun folgt die numerische Berechnung der Hochpunkte.
C++ Programm zur Bestimmung der Hochpunkte der FunktionBerechnen Sie die x-Werte der Hochpunkte der Funktion $f(x)$ mittels der Methode der Bisektion (Intervallhalbierungsverfahren) unter Verwendung eines C++ Programms.
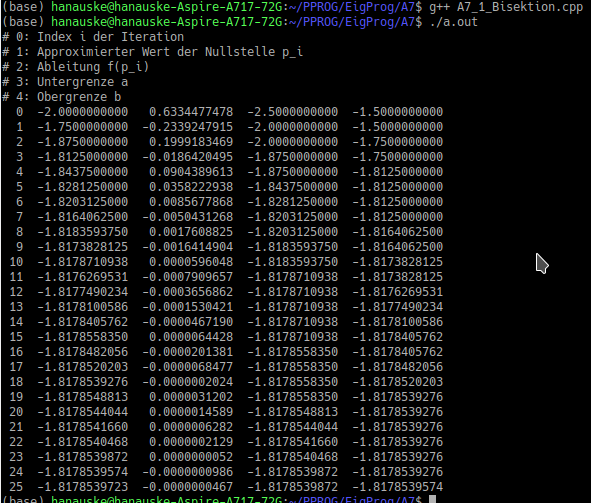
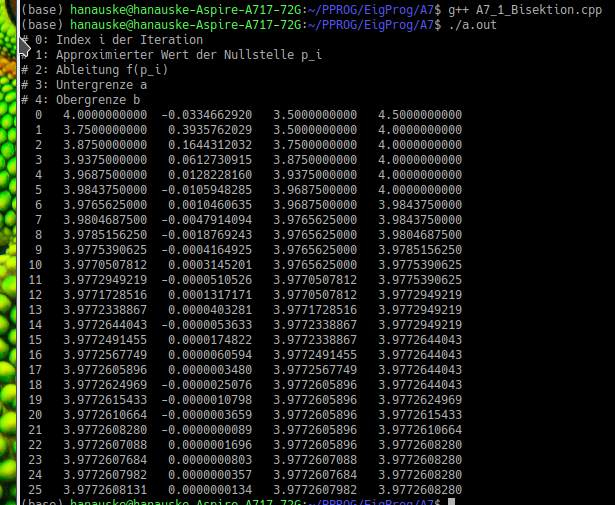
Das folgende C++ Programm berechnet die Hochpunkte der Funktion $f(x)$, wobei die beiden Anfangsintervalle $[a,b]=[-2.5, -1.5]$ und $[a,b]=[3.5, 4.5]$ anhand der Grafik der Funktion abgeschätzt wurden.
// Musterlösung der Aufgabe 1 des Übungsblattes Nr.7 /* Mittels der Methode der Bisektion (Intervallhalbierungsverfahren) * werden die beiden Maxima der Funktion f(x) approximiert: f_strich=0 . * Der Ausdruck der Ableitung (f_strich) wurde aus dem Jupyter Notebook A7_1.ipynb kopiert * und die Werte der Obergrenze und Untergrenze des anfaenglichen Teilintervalls [a,b] * wurde mittels der grafischen Veranschaulichung von f_strich im Jupyter Notebook festgelegt */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) double f_strich(double x, double q) { // Deklaration und Definition der Ableitung der Funktion f_strich(x) double wert; wert = ( -20*x * ( q - 2*pow(x,2) ) * sin(x/10) + 5*x * ( q*pow(x,2) - pow(x,4) + 5) * sin(x/10) + ( pow(x,4) - q*pow(x,2) - 5 ) * cos(x/10) ) * exp(-pow(x,2)/4)/10 ; return wert; // Rueckgabewert der Funktion f_strich(x) } // Ende der Funktion f_strich(x) int main(){ // Hauptfunktion double q = 9; // Deklaration und Festlegung des Parameter q // double a = 3.5; // Untergrenze des Intervalls [a,b] in dem f(x)=0 gelten soll (fuer Hochpunkt 1) // double b = 4.5; // Obergrenze des Intervalls [a,b] in dem f(x)=0 gelten soll (fuer Hochpunkt 1) double a = -2.5; // Untergrenze des Intervalls [a,b] in dem f(x)=0 gelten soll (fuer Hochpunkt 2) double b = -1.5; // Obergrenze des Intervalls [a,b] in dem f(x)=0 gelten soll (fuer Hochpunkt 2) const int N = 25; // Anzahl der Iterationen im Intervallhalbierungsverfahren double p, fp; // Deklaration der Variablen des approximierten x- und f_strich(x)-Wertes der Nullstelle double fa=f_strich(a,q); // Deklaration und Initialisierung des Funktionswertes f_strich(a) an der Untergrenze printf("# 0: Index i der Iteration \n# 1: Approximierter Wert der Nullstelle p_i \n"); // Beschreibung der ausgegebenen Groessen printf("# 2: Ableitung f(p_i) \n"); // Beschreibung der ausgegebenen Groessen printf("# 3: Untergrenze a \n# 4: Obergrenze b \n"); // Beschreibung der ausgegebenen Groessen for(int i=0; i<=N; ++i){ // Schleifen Anfang p = a + (b-a)/2; // Festlegung des x-Wertes in der Mitte des Intervalls [a,b] (x=p) fp = f_strich(p,q); // Berechnung des f_strich(p)-Wertes in der Mitte des Intervalls [a,b] printf("%3d %14.10f %14.10f %14.10f %14.10f \n",i, p, fp, a, b); // Ausgabe der berechneten Werte if( fa*fp > 0 ){ // Falls der berechnete Wert f_strich(p) das gleiche Vorzeichen hat wie f_strich(a), dann ... a = p; // ... setze die Untergrenze auf a=p und ... fa = fp; // ... lege den neuen Funktionswert an der Untergrenze fest: f_strich(a)=f_strich(p) } else if( fa*fp < 0 ){ // Falls der berechnete Wert f_strich(p) ein unterschiedliches Vorzeichen hat wie f(a), dann ... b = p; // ... setze die Obergrenze auf b=p } else{ // Falls durch der berechnete Funktionswert gerade Null ist (f_strich(p)=0 -> f_strich(a)*f_strich(p)=0), dann ... i = N; // ... beende das Bisektion-Verfahren vorzeitig } // else Ende } // Ende der for-Schleife des Bisektion-Verfahres }
Führt man das Programm mit dem Anfangsintervall $[a,b]=[-2.5, -1.5]$ ( $[a,b]=[3.5, 4.5]$ ) aus, so erhält man die linke (rechte) Terminalausgabe:
Musterlösung zur Aufgabe 2 (10 Punkte)
Diese Aufgabe ist angelehnt an das Kapitel 23 "Der gedämpfte harmonische Oszillator" des Buches von Prof. Walter Greiner, Mechanik (Teil 1) [5. Auflage, 1989, siehe Seite 226- 237]. Siehe auch Vorlesungsskript von Prof. Rischke auf Seite 117- 126 http://www.th.physik.uni-frankfurt.de/~drischke/Skript_MI_WiSe2016-2017.pdf ). Wir betrachten im Folgenden den gedämpften harmonischen Oszillator am Beispiel eines reibungsfrei gelagerten Wagens (Masse=$M$) auf den eine Rückstellkraft einwirkt (die proportional zu seiner Auslenkung $x$ ist (Proportionalitätskonstante $k$)), wobei zusätzlich eine geschwindigkeitsabhängige Reibungskraft auf den Wagen einwirkt (z.B. verursacht durch den auf den Wagen einwirkende Luftwiderstand, Stokesscher Ansatz: Proportionalitätskonstante $\alpha$). Aufgrund der Rückstellkraft, besitzt das zugrundeliegende Potential $V(x)$ die Form einer Parabel $V(x)=\frac{k \, x^2}{2}$. Die Differentialgleichung des linearen harmonischen Oszillators mit Dämpfung wird mittels der folgenden Differentialgleichung zweiter Ordnung beschrieben (wir setzen $\omega_0^2=\frac{k}{M}$ und $\beta = \frac{\alpha}{2M}$): $$ \begin{equation} \ddot{x}(t) = - \omega_0^2 \, x(t) - 2 \beta \, \dot{x}(t) \end{equation} $$ Die Anfangsbedingungen seien zunächst noch allgemein gehalten: $x(0) = \alpha_1 \,\, , \,\, \dot{x}(0) = \alpha_2$. Bestimmen Sie die allgemeine Lösung der Differentialgleichung mittels eines eigenen Jupyter Notebooks. Geben Sie dann die spezielle Lösung der Differentialgleichung bei festgelegten Parameterwerten ($\omega_0^2=3$ und $\beta = 0.25$) und Anfangsbedingungen ($\alpha_1 = 0$ und $\alpha_2 = 40$) an und visualisieren Sie diese in einem x-t Diagramm. An welchem Ort befindet sich der Wagen zur Zeit $t=10$ ( $x(10)$ )?
Das nebenstehende Jupyter Notebook A7_2.ipynb (siehe A7_2.html) stellt die Musterlösung der Aufgabe dar.