Musterlösung zum Übungsblatt Nr. 6
Musterlösung zur Aufgabe 1 (6.5 Punkte)
Der unten abgebildete C++ Quelltext stellt die Musterlösung zur Aufgabe 2 dar. Die ersten 40 Zahlenwerte der Fibonacci-Folge wurden in einem eindimensionalen C++ Array gespeichert, das am Anfang des Programms zunächst deklariert wurde 'unsigned int f[N];'. Danach wurden die ersten beiden Folgenglieder mit '1' initialisiert. Die eigentliche Implementierung des rekursiv definierten Bildungsgesetzes der Fibonacci-Folge wurde dann mittels der Indexschreibweise innerhalb der for-Schleife realisiert:
$f_n = f_{n-1} + f_{n-2} \, \Rightarrow \quad$ f[n] = f[n-1] + f[n-2];
Das Verhältnis zweier aufeinanderfolgender Zahlen der Fibonacci-Folge ($\frac{f_n}{f_{n-1}}$), welches im Grenzwert $\lim \limits_{n \to \infty}$ gegen die irrationale Zahl des Goldenen Schnitts $\Phi \approx 1.618033988749894848204586834$ konvergiert, wurde mittels des folgenden Ausdrucks im Terminal ausgegeben: (double)(f[n])/f[n-1]
Man erkennt hierbei deutlich, das die mathematische Formulierung und die C++ Array-Indexschreibweise deutliche Ähnlichkeiten besitzt.
/* Musterlösung der Aufgabe 1 des Übungsblattes Nr.6 * Fibonacci-Folge mittels eines eindimensionalen Arrays * und Vergleich mit der irrationalen Zahl des Goldenen Schnitts */ #include <iostream> // Ein- und Ausgabebibliothek int main(){ // Hauptfunktion const unsigned int N = 40; // Deklaration und Initialisierung des maximalen Folgengliedes unsigned int f[N]; // Deklaration der Fibonacci-Zahlen als ein eindimensionales Array f[0]=1; // Initialisierung des 0.ten Folgengliedes f[1]=1; // Initialisierung des 1.ten Folgengliedes printf("# 0: Folgenindex n \n# 1: Fibonacci Zahl \n# 2: Goldener Schnitt \n"); // Beschreibung der ausgegebenen Groessen printf("%4i %12i \n",0,f[0]); // Ausgabe des 0. Folgengliedes printf("%4i %12i \n",1,f[1]); // Ausgabe des 1. Folgengliedes for(int n=2; n<N; ++n){ // Schleifen Anfang f[n] = f[n-1] + f[n-2]; // Rekursives Bildungsgesetz der Fibonacci-Folge printf("%4i %12i %20.17f \n",n, f[n], (double)(f[n])/f[n-1]); // Ausgabe der berechneten Groessen } // Ende der Schleife printf("# Approximierte irrationale Zahl des Goldenen Schnitts: %20.17f \n", (double)(f[N-1])/f[N-2]); printf("# Wirklicher Zahlenwert des Goldenen Schnitts : %20.17Lf \n", 1.618033988749894848204586834L); }
Musterlösung zur Aufgabe 2 (7 Punkte)
Für die Vektoren $\vec{a}$ und $\vec{b}$ \[ \begin{equation} \vec{a} =\left( \begin{array}{ccc} 2.3 \\ -1.36 \\ 6.91 \end{array} \right) \quad , \quad \vec{b} =\left( \begin{array}{ccc} 10.3 \\ -4.34 \\ 5.3 \end{array} \right) \end{equation} \] wurde das Skalar- und Kreuzprodukt mittels der folgenden Ausdrücke bestimmt: \[ \begin{eqnarray} \hbox{Skalarprodukt:} && s = \vec{a} \cdot \vec{b} = \sum_{i=1}^3 a_i \, b_i \\ \hbox{Kreuzprodukt:} && \vec{c} = \vec{a} \times \vec{b} = \sum_{i,j,k=1}^3 \epsilon_{ijk} \, a_i \, b_j \, \vec{e}_k \quad , \end{eqnarray} \] wobei $\epsilon_{ijk}$ der total antisymmetrischer Tensor (auch Epsilon-Tensor bzw. Levi-Civita-Symbol) ist. Das folgende C++ Programm stellt den Quelltext der Musterlösung dar.
/* Musterlösung der Aufgabe 2 des Übungsblattes Nr.6 * Skalarprodukt und Kreuzprodukt zweier Vektoren * deklariert mittels zweier eindimensionaler Arrays */ #include <iostream> // Ein- und Ausgabebibliothek int main(){ // Hauptfunktion double a[] = { 2.3, -1.36, 6.9}; // Definition des Vektors a mittels eines double-Arrays double b[] = {10.3, -4.34, 5.3}; // Definition des Vektors b mittels eines double-Arrays double c_1[3] = {0, 0, 0}; // Deklaration des Vektors c mittels eines double-Arrays (c = a x b) double c_2[3] = {0, 0, 0}; // Deklaration des Vektors c mittels eines double-Arrays (c = a x b) int epsilon[3][3][3]; // Total antisymmetrischer Tensor (Levi-Civita-Symbol, Epsilon-Tensor) double skal_prod_1=0; // Deklaration der Variable fuer das Skalarprodukt a*b mittels Index-Zugriff double skal_prod_2=0; // Deklaration der Variable fuer das Skalarprodukt a*b mittels Zeiger-Zugriff double* pa = a; // Definition des Zeigers auf das double-Array a double* pb = b; // Definition des Zeigers auf das double-Array a double* pc_2 = c_2; // Definition des Zeigers auf das double-Array a // Skalarprodukt a*b for(int i=0; i<3; ++i){ skal_prod_1 = skal_prod_1 + a[i]*b[i]; skal_prod_2 = skal_prod_2 + *(pa+i) * *(pb+i); } printf("Das Skalarprodukt mittels Index-Zugriff: a*b = %8.5f \n", skal_prod_1); printf("Das Skalarprodukt mittels Zeiger-Zugriff: a*b = %8.5f \n", skal_prod_2); // Initialisierung der Werte für den Epsilon-Tensor for(int i=0; i<3; ++i){ for(int j=0; j<3; ++j){ for(int k=0; k<3; ++k){ if (i==j || i==k || j==k){ epsilon[i][j][k] = 0; } else if ( (i==0 && j==1 && k==2) || (i==1 && j==2 && k==0) || (i==2 && j==0 && k==1)){ epsilon[i][j][k] = 1; } else { epsilon[i][j][k] = -1; } } } } // Kreuzprodukt c = a x b for(int i=0; i<3; ++i){ for(int j=0; j<3; ++j){ for(int k=0; k<3; ++k){ c_1[k] = c_1[k] + epsilon[i][j][k] * a[i] * b[j]; *(pc_2+k) = *(pc_2+k) + epsilon[i][j][k] * *(pa+i) * *(pb+j); } } } printf("Das Kreuzprodukt mittels Index-Zugriff: a x b = ( %8.5f , %8.5f, %8.5f ) \n", c_1[0], c_1[1], c_1[2]); printf("Das Kreuzprodukt mittels Zeiger-Zugriff: a x b = ( %8.5f , %8.5f, %8.5f ) \n", c_2[0], c_2[1], c_2[2]); }
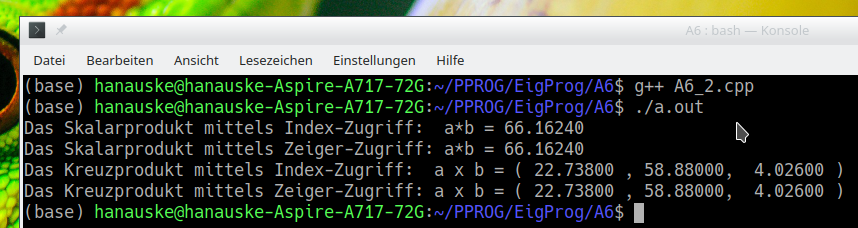
Es wurden zunächst die angegebenen Vektoren $\vec{a}$ und $\vec{b}$ als eindimensionale C++ Array und auch zwei entsprechende Zeigervariablen (double* pa = a; und double* pb = b; ) definiert. Es wurde dann das Skalarprodukt mittels eines Indexzugriffs ( skal_prod_1 = skal_prod_1 + a[i]*b[i]; ) bzw. Zeigerzugriffs ( skal_prod_2 = skal_prod_2 + *(pa+i) * *(pb+i); ) realisiert. Dann wurde der schon oben deklarierte Epsilon-Tensor $\epsilon_{ijk}$ mittels dreier geschachtelter for-Schleifen initialisiert. Die darauf folgende Berechnung des Kreuzproduktes wurde ebenfalls mittels eines Indexzugriffs ( c_1[k] = c_1[k] + epsilon[i][j][k] * a[i] * b[j]; ) bzw. Zeigerzugriffs ( *(pc_2+k) = *(pc_2+k) + epsilon[i][j][k] * *(pa+i) * *(pb+j); ) realisiert. Die nebenstehende Abbildung zeigt die Terminalausgabe des Programms.
Musterlösung zur Aufgabe 3 (6.5 Punkte)
Das unten abgebildete C++ Programm, berechnet mittels einer modifizierten Newton-Raphson Methode die Nullstelle der Funktion $f(x) = e^x - 20$). Für den approximativen Wert der Ableitung wurde einerseits die 'Dreipunkte-Mittelpunkt-Formel' und die 'Fünfpunkte-Mittelpunkt-Formel' verwendet und zusätzlich die Ergebnisse mit einer Berechnung verglichen, die den analytischen Ausdruck für $f^\prime(x)$ benutzt.
// Musterlösung der Aufgabe 3 des Übungsblattes Nr.6 #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) double f(double x) { // Deklaration und Definition der Funktion f(x) double wert; // Lokale double-Variable (nur im Bereich der Funktion gültig) wert = exp(x) - 20; // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } // Ende der Funktion f(x) double f_strich_analyt(double x) { // Deklaration und Definition der Funktion f(x) double wert; // Lokale double-Variable (nur im Bereich der Funktion gültig) wert = exp(x); // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } // Ende der Funktion f(x) int main(){ // Hauptfunktion double p[3] = {2, 2, 2}; // Deklaration des approximierten x-Wertes der Nullstelle und Start-Initialisierung const int N=10; // Anzahl der Iterationen in der Newton-Raphson Methode double h = 0.1; // Aequidistanter Abstand zwischen den x-Werten die zur numerischen Differentation benutzt werden const double p_null = log(20); // Beschreibung der ausgegebenen Groessen printf("# 0: Index i der Iteration i \n# 1: Approximierter Wert der Nullstelle p_i \n"); printf("# 2: Dreipunkte-Mittelpunkt-Formel \n# 3: Fuenfpunkte-Mittelpunkt-Formel \n"); printf("# 4: Relativer Fehler zum wirklichen Wert |(p-p_0)/p| \n# 5: Relativer Fehler zum wirklichen Wert |(p-p_1)/p| \n"); printf("# 6: Relativer Fehler zum wirklichen Wert |(p-p_2)/p| \n"); for(int i=0; i<N; ++i){ // For-Schleife der Newton-Raphson Methode printf("%3d %20.14f %20.14f %20.14f %20.14f %20.14f %20.14f \n",i, p[0], p[1], p[2], fabs((p_null-p[0])/p_null), fabs((p_null-p[1])/p_null), fabs((p_null-p[2])/p_null)); p[0] = p[0] - f(p[0])/f_strich_analyt(p[0]); // Newton-Raphson Methode mit analytischer Ableitung f'(x) p[1] = p[1] - f(p[1])/( (f(p[1]+h) - f(p[1]-h))/(2*h) ); // Newton-Raphson Methode, Dreipunkte-Mittelpunkt-Formel fuer f' p[2] = p[2] - f(p[2])/( (f(p[2]-2*h) - 8*f(p[2]-h) + 8*f(p[2]+h) - f(p[2]+2*h))/(12*h) ); // Newton-Raphson Methode, Fuenfpunkte-Mittelpunkt-Formel fuer f' } // Ende der For-Schleife der Newton-Raphson Methode printf("# Wirklicher Wert der Nullstelle: %20.14f \n", p_null); }
Das Programm erzeugt die folgende Terminalausgabe.
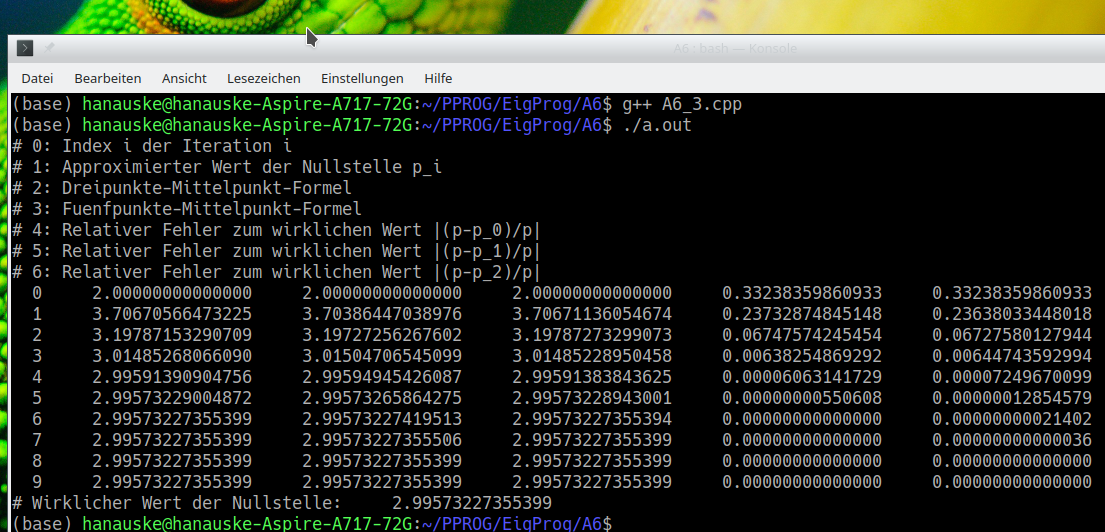
Man erkennt, dass das Konvergenzverhalten der 'Dreipunkte-Mittelpunkt-Formel' ein wenig schlechter als das der 'Fünfpunkte-Mittelpunkt-Formel' ist. Die berechneten Nullstellenwerte der 'Fünfpunkte-Mittelpunkt-Formel' unterscheiden sich nur unmerklich von den Werte, die sich mittels der Berechnung mit analytischer $f^\prime(x)$ Funktion ergeben.