Lorenz system
An interactive simulation of a chaotic attractor
created by Hendrik Wernecke
— summer term 2018 —
— summer term 2018 —
The Lorenz system was defined by Lorenz [1] and is very important.
Simulation
time $t = $0.00
$\rho=$
Usage
This simulation is damn hard to use. Press the START button and it runs. Press STOP and it stops.Theory
This is the Lorenz system:
\begin{align}
\dot{x} &= \sigma(y-x)\\
\dot{y} &= x(\rho-z)-y\\
\dot{z} &= xy-\beta z\,.
\end{align}
We use $\beta=8/3$ and $\sigma=10$ and keep $\rho$ as a parameter
The syste has the following fixed points
\begin{align}
\mathbf{v}_\text{o} &= (0,0,0)\\
\mathbf{v}_{1,2} &= \left(\pm\sqrt{\beta(\rho-1)},\pm\sqrt{\beta(\rho-1)},\rho-1\right)
\end{align}
which are also indicated on the canvas.
For $r=28$ the Lorenz system is chaotic and then it looks like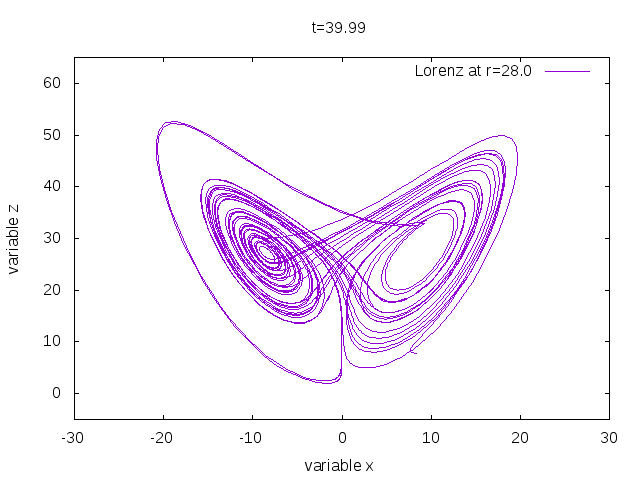
For $r=28$ the Lorenz system is chaotic and then it looks like

Figure: The Lorenz butterfly.
Code & documentation
Here I want to show some parts of the JavaScript code that I am fond of:- solving the Lorenz ODE by Euler integration
- the core drawing function looks like this
Acknowledgements, authors & contact
Acknowledgements The author would like to thank everyone.About the authors Hendrik Wernecke is a PhD student in the group of Prof. C. Gros at Goethe University Frankfurt (Main).
Contact For questions, suggestions or comments on this simulation, please contact click to show email
References & further reading
- [1]
- : Deterministic nonperiodic flow., J. Atmos. Sci. 20(2) 1963.
Legal note: We do not take any responsibility for
the content of the webPages linked here-in.