automatic gradient evaluation
- AutoGrad: automatic evaluation of gradients
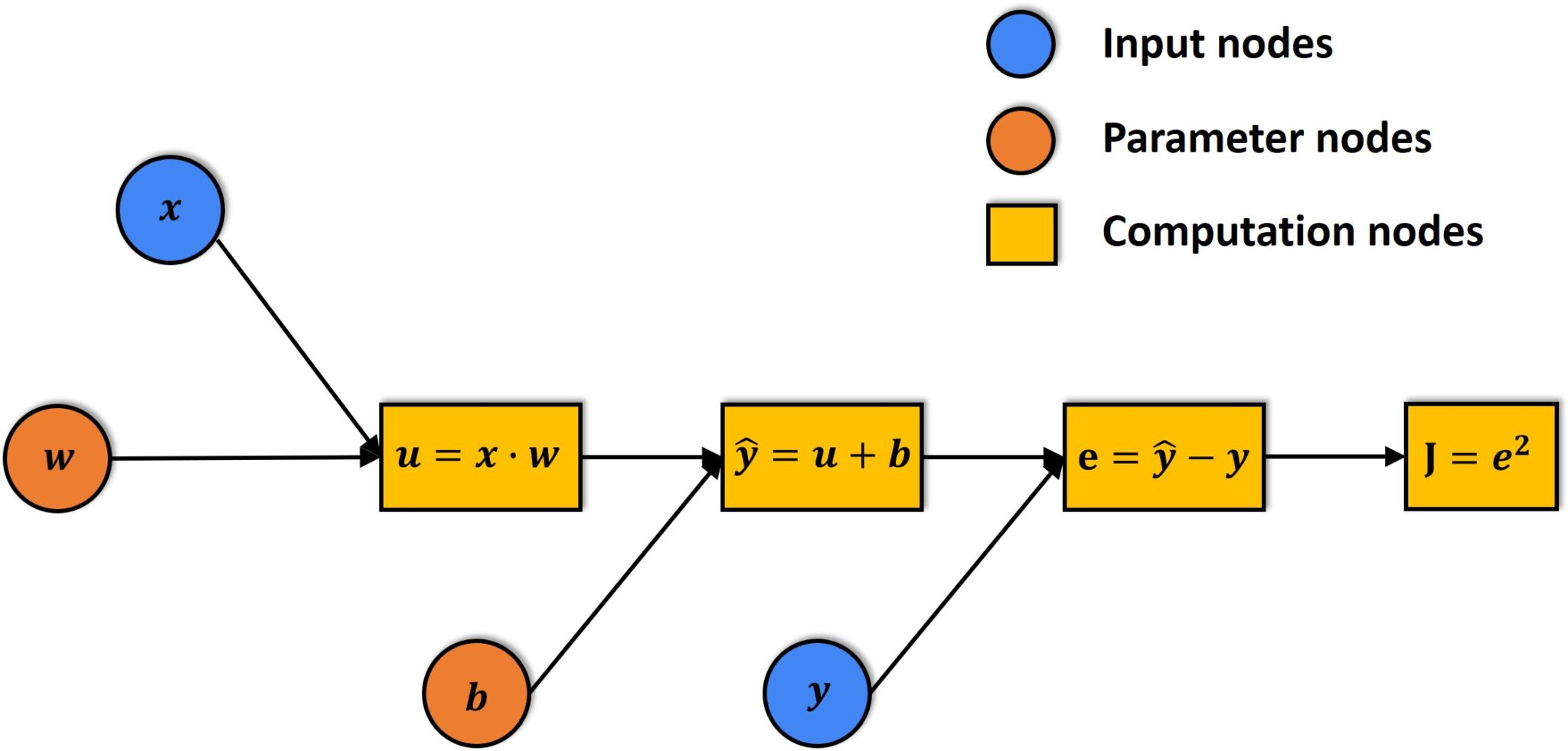
- computation graph
:: nodes as tensors
:: edges as functions mapping tensors to tensors - backward pass
evaluates gradients for tensors with
requires_grad = True
:: add to previous gradient (if existing) -
detach(temporarily) tensors for 'by hand' operations,
viz for operations outside the compuation graph
:: temporarily settingrequires_grad = False -
with torch.no_grad():
:: detach everything inside following scope
Copy
Copy to clipboad
Downlaod
Download
#!/usr/bin/env python3
import torch # PyTorch needs to be installed
dim = 2
eps = 0.1
x = torch.ones(dim, requires_grad=True) # leaf of computational graph
print("x : ",x)
print("x.data : ",x.data)
print("x[0] : ",x[0])
print("x[0].item() : ",x[0].item())
print()
y = x + 2
out = torch.dot(y,y) # scalar product
print("y : ",y)
print("out : ",out)
print()
out.backward() # backward pass --> gradients
print("x.grad : ",x.grad)
with torch.no_grad(): # detach from computational graph
x -= eps*x.grad # updating parameter tensor
x.grad = None # flush
print("x : ",x.data)
print("\n#---")
print("#--- .backward() adds new gradient to old gradient")
print("#--- convenient for batch updating")
print("#---\n")
y = torch.zeros(dim, requires_grad=True)
torch.dot(y+1,y+1).backward()
print("y.grad : ",y.grad)
torch.dot(y+1,y+1).backward()
print("y.grad : ",y.grad)
torch.dot(y+1,y+1).backward()
print("y.grad : ",y.grad)
torch.dot(y+1,y+1).backward()