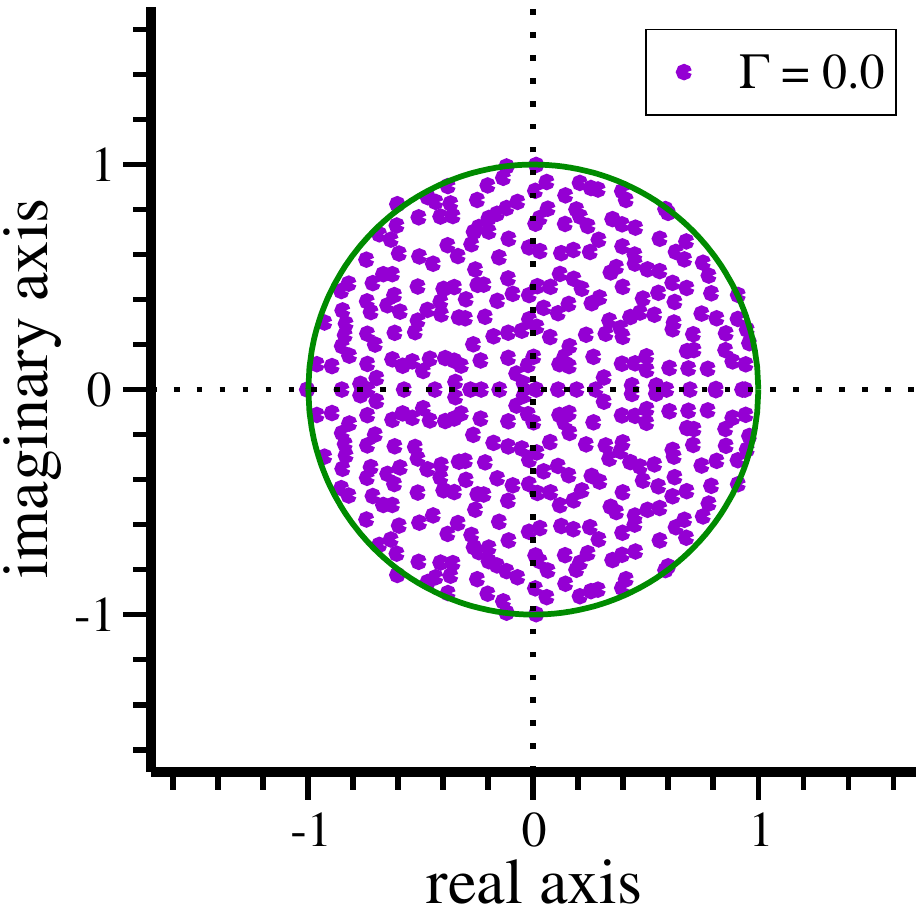
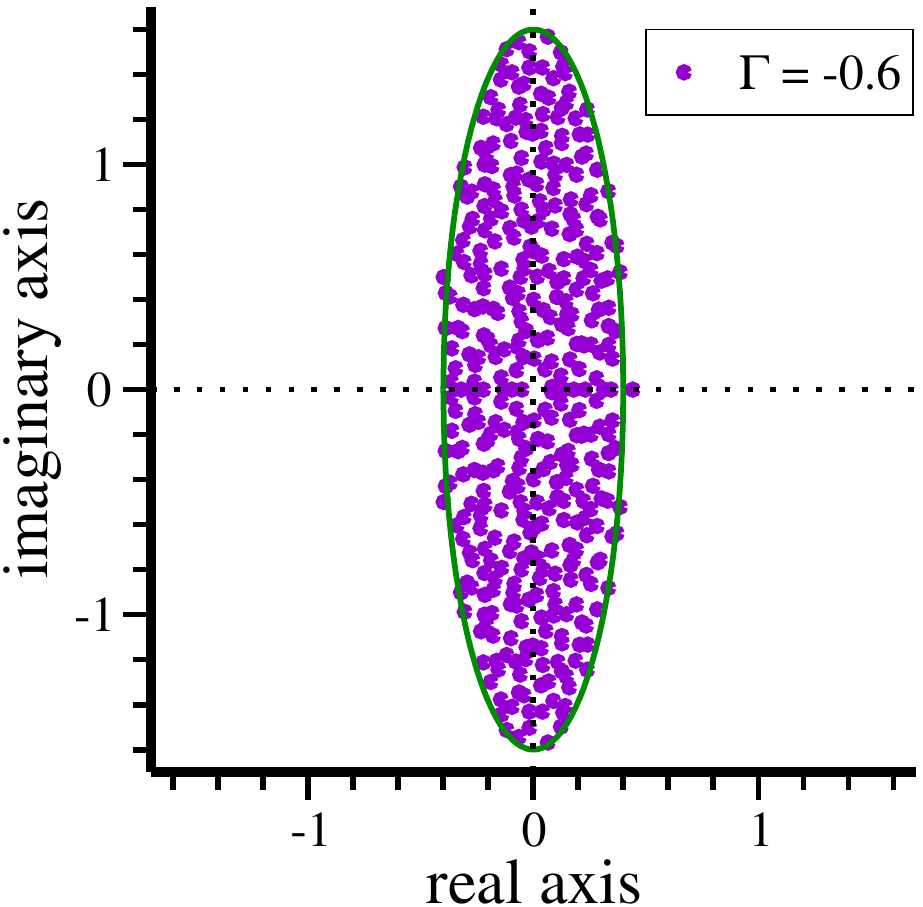
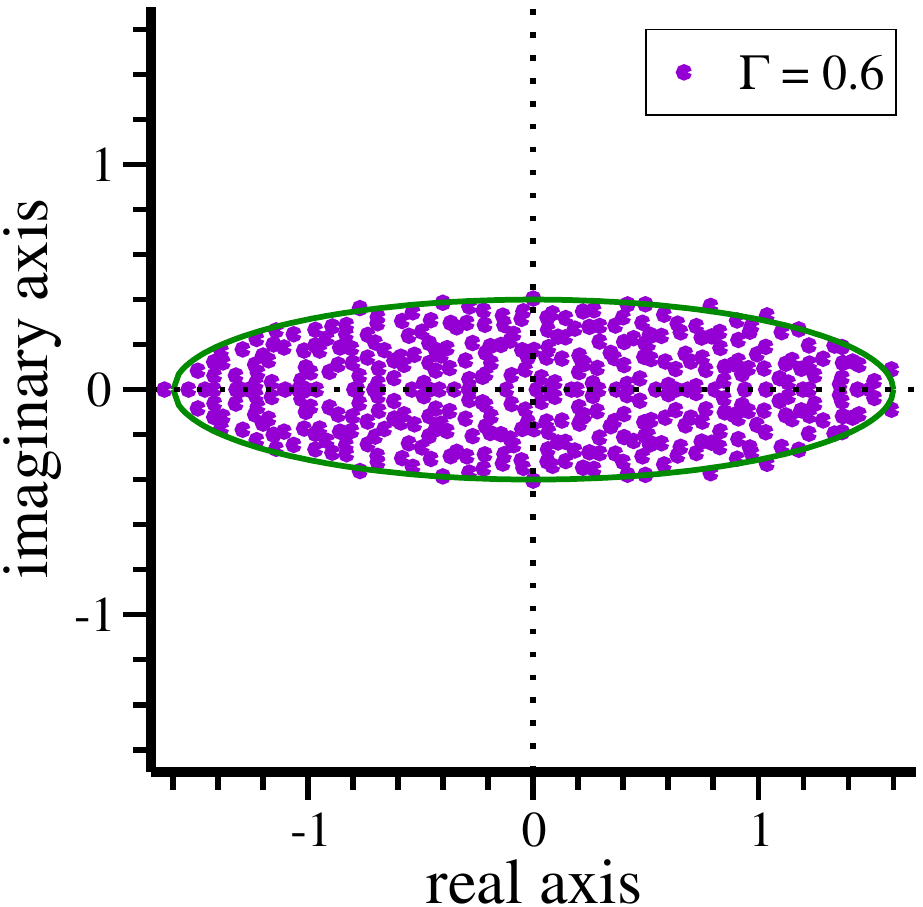
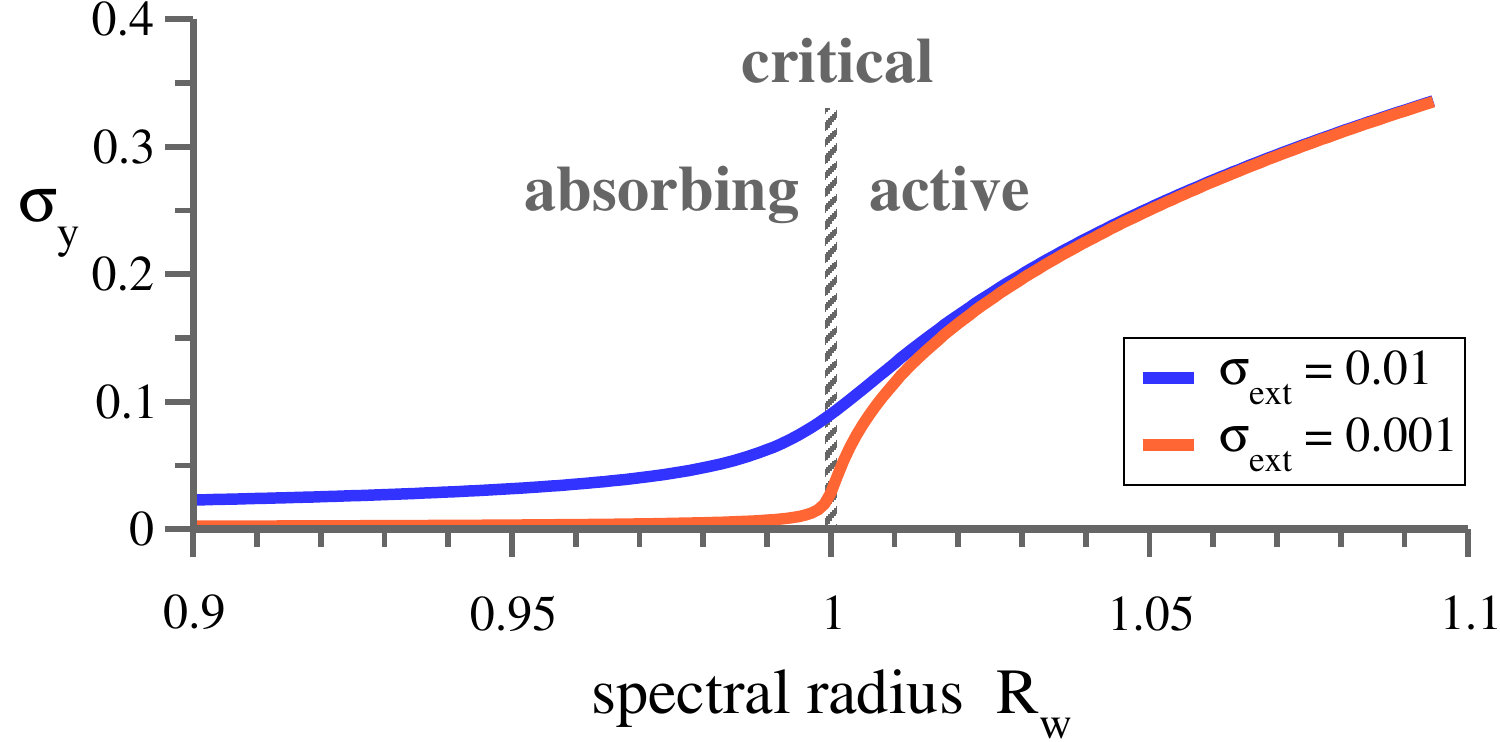
#!/usr/bin/env python3
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

def target_function(n):
  "to be reproduced"
  series = np.zeros(n)
  for i in range(n):
    x = i*200.0/n
    series[i] = np.sin(x) + np.cos(0.3*(x+np.sin(1.1*x)))
  return series


class EchoStateNetwork:
  "Echo State Network class"
  def __init__(self, input_size, reservoir_size,
               output_size, spectral_radius=0.9,
               sparsity=0.1):
    self.reservoir_size  = reservoir_size
    self.spectral_radius = spectral_radius

# input weights
    self.Win = torch.randn(reservoir_size, input_size)*0.1

# sparse reservoir weights
    W = torch.randn(reservoir_size, reservoir_size)
    W[torch.rand_like(W) > sparsity] = 0.0

# scaling reservoir weights to set spectral radius
    eigenvalues = torch.linalg.eigvals(W).abs()
    W *= spectral_radius / eigenvalues.max()
    self.W = W

# output weights (initialized later during training)
    self.Wout = torch.randn(reservoir_size + 1,
                output_size, requires_grad=True)

  def forward(self, input_series):
    """running the ESN for the entire input series, 
       collects the reservoir states"""
    states = []
    state = torch.zeros(self.reservoir_size)

    for u in input_series:      # @: matrix multiplication
      state = torch.tanh(self.Win@u + self.W@state)
      states.append(state)
    return torch.stack(states)  # list to tensor

  def train(self, input_series, target_series,
            learning_rate=5e-3, epochs=5000):
    """ reservoir weights do not change 
        --> reservoir states do not change
        --> reservoir states can be evoulated
            before training
    """
    states = self.forward(input_series)
# adding bias 
    states_with_bias =\
       torch.cat([states, torch.ones(states.shape[0], 1)],
                 dim=1)

# instantiate optimizer / loss function
    optimizer = torch.optim.SGD([self.Wout],
                lr=learning_rate)
    loss_fn = nn.MSELoss()

# optimizing output weight
    for epoch in range(epochs):
      optimizer.zero_grad()
      predictions = states_with_bias@self.Wout
      loss = loss_fn(predictions, target_series)
      loss.backward()
      optimizer.step()
      if (epoch+1)%100==0:
        print(f'Epoch {epoch+1}/{epochs},', end="")
        print(f' Loss {loss.item():9.5f}')

  def predict(self, input_series):
    states = self.forward(input_series)
    states_with_bias = torch.cat([states,
       torch.ones(states.shape[0], 1)], dim=1)
    return states_with_bias @ self.Wout

# generating time series train/test data
data = target_function(2000)
train_data, test_data = data[:1500], data[1500:]

# preparing input and target series for the ESN
train_input  = torch.tensor(train_data[:-1],
               dtype=torch.float32).view(-1, 1)
train_target = torch.tensor(train_data[1:],
               dtype=torch.float32).view(-1, 1)
test_input   = torch.tensor(test_data[:-1],
               dtype=torch.float32).view(-1, 1)
test_target  = torch.tensor(test_data[1:],
               dtype=torch.float32).view(-1, 1)

# initialize and train the ESN
esn = EchoStateNetwork(input_size=1,
                       reservoir_size=500,
                       output_size=1)
esn.train(train_input, train_target)

# predictions/performance for test data
predictions = esn.predict(test_input)
mse = nn.MSELoss()(predictions, test_target)
print(f"\nmean squared test error: {mse.item()}")

# plotting results
plt.figure(figsize=(12, 6))
plt.plot(test_target.numpy(), label="true")
plt.plot(predictions.detach().numpy(), label="predicted")
plt.legend()
plt.title("ESN inference")
plt.show()