#!/usr/bin/env python3
#
# complete small transfomer
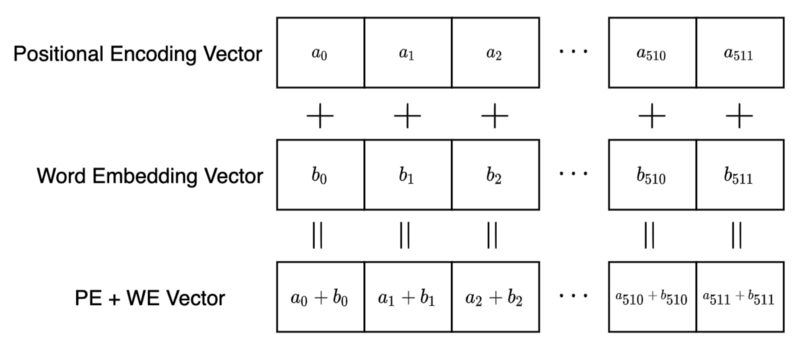
# :: no positional embedding
# :: no beam search, greed prediction
#
# read text from data.txt
#
import torch
import math
import random
import pickle # serialization
import matplotlib.pyplot as plt
nLayer = 1 # number of layers
nContext = 16 # context length
dim = 10 # embedding dimension, set later
nBatch = 20 # batch size
nEpoch = 2000 # number of epochs
learning_rate = 2.0e-2
load_model = False # load dumped model
#
# cpu or gpu
#
myDevice = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
#myDevice = 'cpu'
print("# device used : ", myDevice)
#
# transfomer bilayer: attention plus token-wise feed-forward net
#
class transformerBilayer(torch.nn.Module):
""" The second part of the transformer bilayer,
the token-wise feedforward net, expands and contracts:
W_expand -> W_contract, standard by a factor 4 """
def __init__(self, dim, nContext, expand=4):
super().__init__()
self.Q_mat = torch.randn(nContext,dim,dim,
requires_grad=True,device=myDevice)
self.K_mat = torch.randn(nContext,dim,dim,
requires_grad=True,device=myDevice)
self.V_mat = torch.randn(nContext,dim,dim,
requires_grad=True,device=myDevice)
#
mySigma = 1.0/(dim*dim)
torch.nn.init.normal_(self.Q_mat, mean=0.0, std=mySigma)
torch.nn.init.normal_(self.K_mat, mean=0.0, std=mySigma)
torch.nn.init.normal_(self.V_mat, mean=0.0, std=mySigma)
#
self.W_expand = torch.randn(nContext,dim*expand,
dim,requires_grad=True,device=myDevice)
self.W_contract = torch.randn(nContext,dim,dim*expand,
requires_grad=True,device=myDevice)
mySigma = 1.0/(dim*dim*expand)
torch.nn.init.normal_(self.W_expand , mean=0.0, std=mySigma)
torch.nn.init.normal_(self.W_contract, mean=0.0, std=mySigma)
#
self.W_bias = torch.zeros(nContext,dim*expand,
requires_grad=True,device=myDevice)
#
self.nContext = nContext
self.dim = dim # embedding
self.expand = expand # FFN expansion factor
#
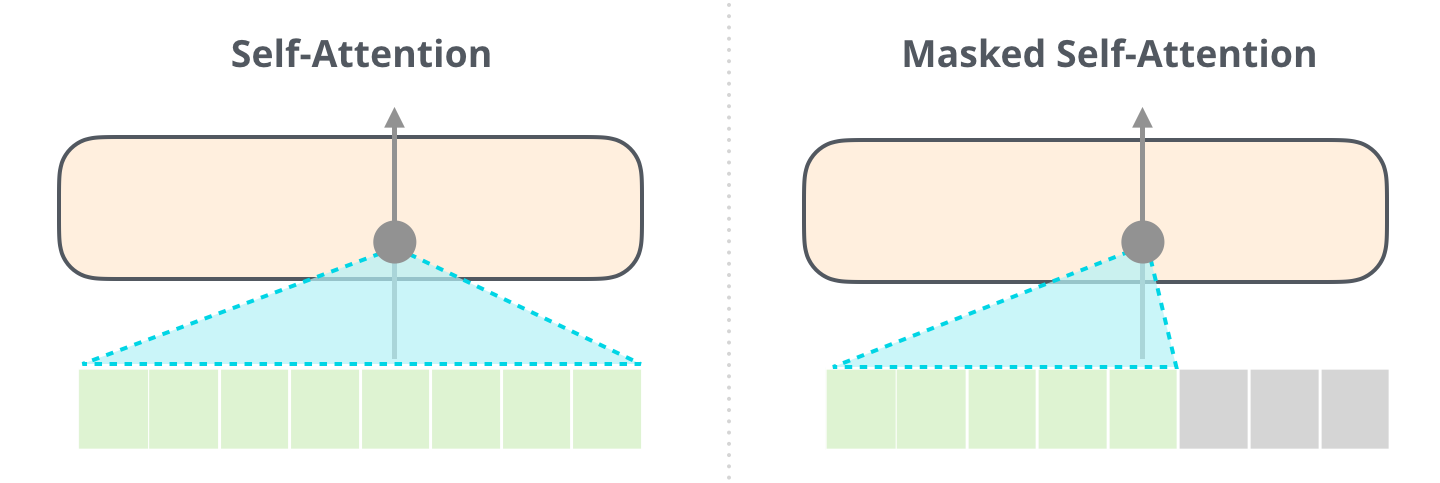
self.paddingMask = torch.ones(nContext,nContext,device=myDevice)
for ii in range(nContext):
for jj in range(ii+1,nContext):
self.paddingMask[ii][jj] = 0.0
def layerNorm(self, x):
mean = torch.sum(x, 0) / self.nContext # sum over rows
sigma = torch.sqrt(torch.square(x-mean).sum() / self.nContext)
return (x-mean)/sigma # for all rows
def feedForward_subLayer(self, x): # bbm 'batch mat mult'
hidden = torch.bmm(self.W_expand,x.unsqueeze(2))\
+ self.W_bias.unsqueeze(2)
hidden = torch.tanh(hidden) # non-linearity
y = torch.matmul(self.W_contract,hidden)
return y.squeeze(2) + x
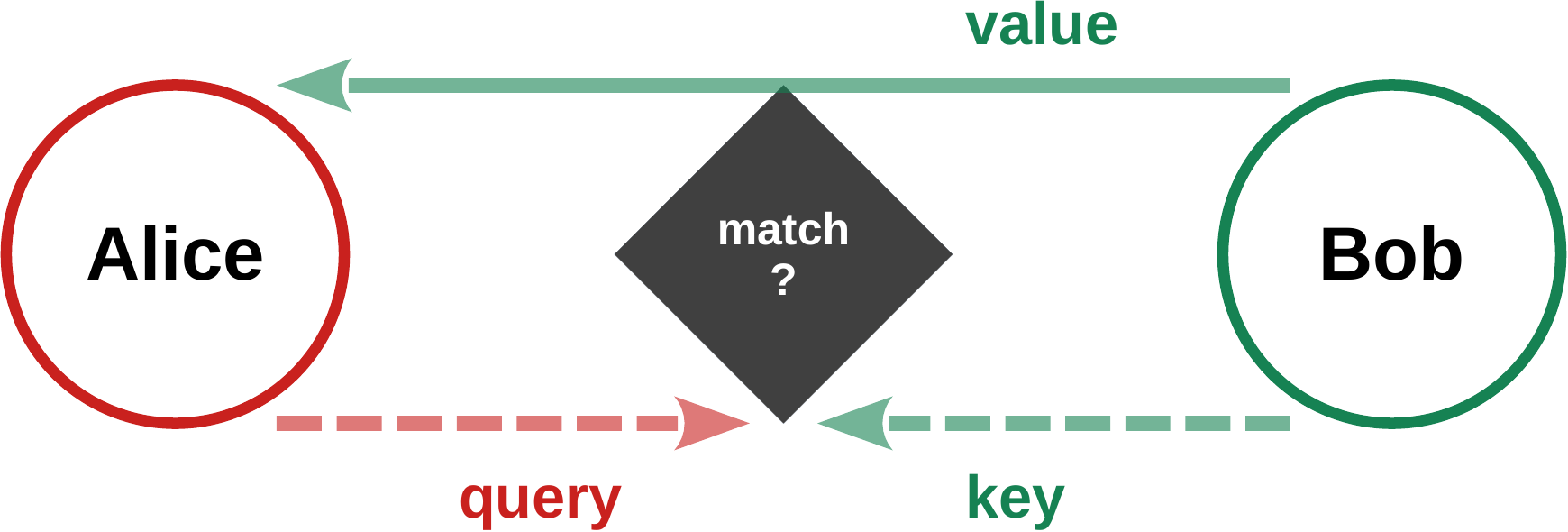
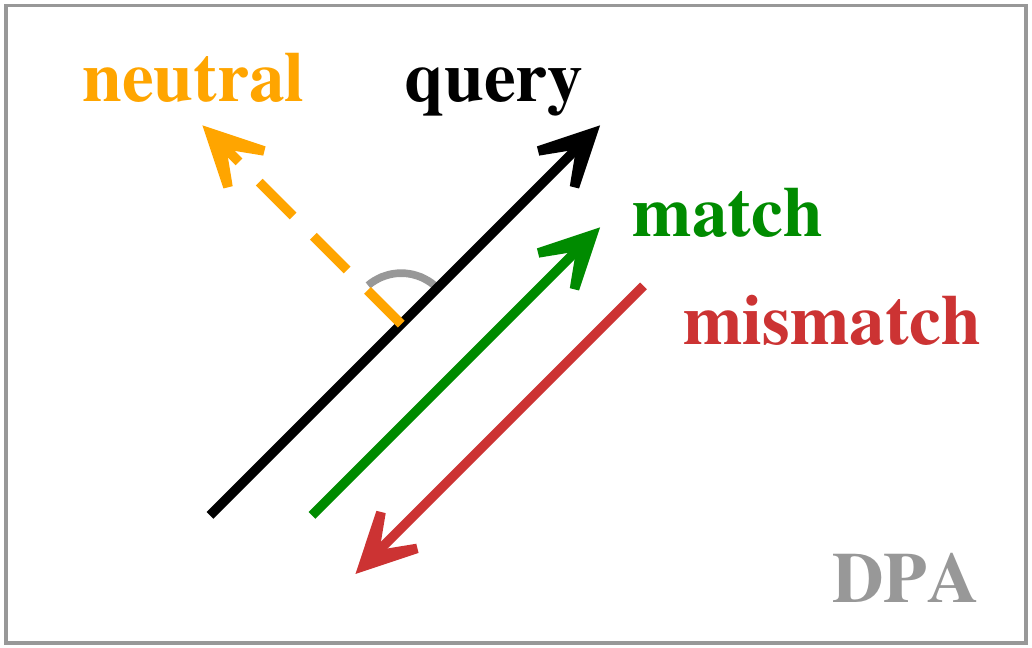
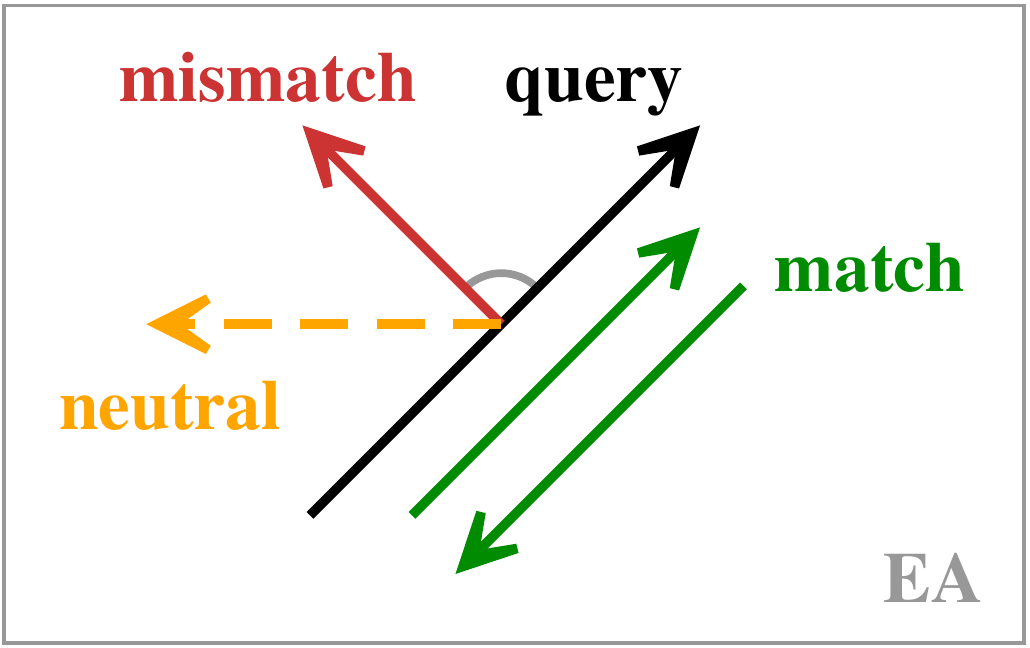
def attention_subLayer(self, x):
QQ = torch.bmm(self.Q_mat,x.unsqueeze(2)).squeeze(2)
KK = torch.bmm(self.K_mat,x.unsqueeze(2)).squeeze(2)
VV = torch.bmm(self.V_mat,x.unsqueeze(2)).squeeze(2)
Q_dot_K = torch.matmul(QQ,torch.transpose(KK,0,1))
# Q_dot_K = torch.inner(QQ,KK) # identical
#
aa = torch.exp(Q_dot_K)*self.paddingMask
alphaTrans = torch.divide(torch.transpose(aa,0,1),aa.sum(1))
alpha_norm = torch.transpose(alphaTrans,0,1)
y = torch.matmul(alpha_norm,VV)
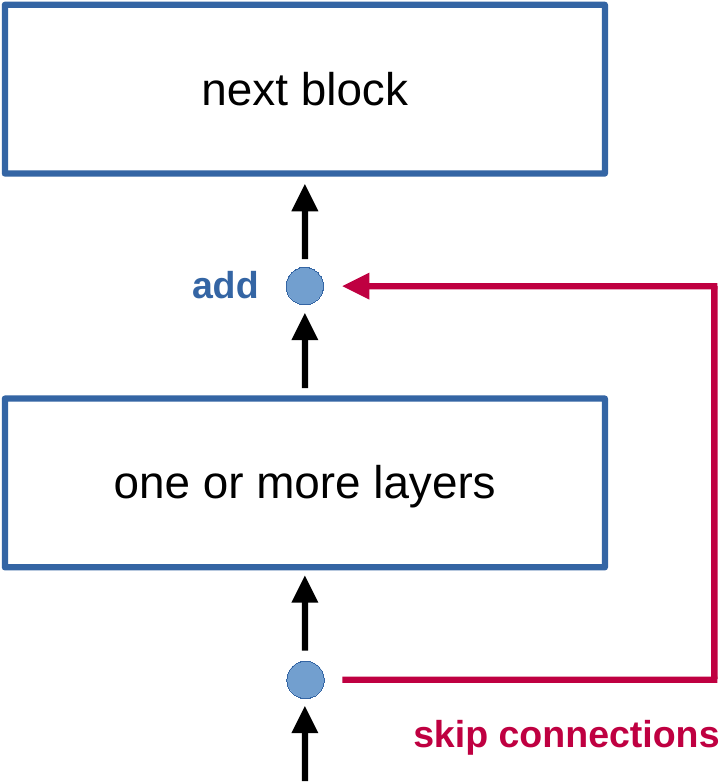
return y + x # skip connections
def forward(self, x):
self.layerNorm(x) # normalization on entry
x = self.attention_subLayer(x)
self.layerNorm(x)
x = self.feedForward_subLayer(x)
return x
def update(self, eps): # updating internal parameters
with torch.no_grad():
self.Q_mat -= eps*self.Q_mat.grad
self.K_mat -= eps*self.K_mat.grad
self.V_mat -= eps*self.V_mat.grad
self.Q_mat.grad = None
self.K_mat.grad = None
self.V_mat.grad = None
self.W_expand -= eps*self.W_expand.grad
self.W_contract -= eps*self.W_contract.grad
self.W_bias -= eps*self.W_bias.grad
self.W_expand.grad = None
self.W_contract.grad = None
self.W_bias.grad = None
#
# load and process training data
#
f_in = open("data.txt", encoding='utf-8-sig')
trainingString = f_in.read()
f_in.close()
trainingString = trainingString.replace("\n", " ") # cleaning
trainingString = trainingString.replace(" ", " ")
trainingText = list(trainingString)
nToken_Data = len(trainingText)
if (1==2):
print("---",trainingString,"---")
trainingString = trainingString.lower() # reducing vocabulary size
vocabulary = list(set(trainingText)) # set contains unique elements
vocabulary.sort() # for reloading model
dim = len(vocabulary) # equal to embedding dimension
print("# vocabulary dimension ", dim)
print("# number of token in data ", nToken_Data)
if (1==1):
print(vocabulary)
#
# embedding dictionary: token (letter) --> tensor
#
letterEmbedding = {letter: torch.zeros(dim,device=myDevice) for letter in vocabulary}
#
# orthogonal embedding tensors (0, ..., 1, 0, ...)
#
count = 0
for letter in vocabulary:
letterEmbedding[letter][count] = 1
count += 1
if (1==2):
print("# ", letterEmbedding)
#
# standard/modified loss function
#
def lossFunction(outputActivity, targetActivity):
lastPos = len(outputActivity)-1
return torch.square(outputActivity[lastPos] - targetActivity[lastPos]).sum()
# return torch.square(outputActivity - targetActivity).sum()
#
# n-idential layer model
#
allLayers = [transformerBilayer(dim,nContext) for iL in range(nLayer)]
def model(x):
for iLayer in range(nLayer):
x = allLayers[iLayer](x)
return x
#
# dump/load model to/from file
#
def dumpLoad(fileName, whatToDo="load", myObject=None):
if (whatToDo=="dump"):
with open(fileName, 'wb') as file:
pickle.dump(myObject, file)
return None
#
if (whatToDo=="load"):
with open(fileName, 'rb') as file:
return pickle.load(file)
#
# load stored trained model
# meta parameters must be identical
#
if (load_model==True):
allLayers = dumpLoad("allLayers.dump")
#
# train on random slices
# shifted for a given batch by 'sride'
#
stride = 1
upperLimit = nToken_Data - nContext - stride*nBatch - 1
training_data = torch.zeros(nContext,dim,device=myDevice)
training_value = torch.zeros(nContext,dim,device=myDevice)
#
for iEpoch in range(1,nEpoch+1):
iStart = random.randrange(upperLimit)
batchLoss = 0.0
for iBatch in range(nBatch):
inputLetters = trainingText[iStart :iStart+nContext]
targetLetters = trainingText[iStart+1:iStart+nContext+1]
iStart += stride
if (1==2):
print()
print(inputLetters)
print(targetLetters)
for iC in range(nContext):
training_data[iC] = letterEmbedding[ inputLetters[iC]]
training_value[iC] = letterEmbedding[targetLetters[iC]]
loss = lossFunction(model(training_data),training_value)
loss.backward()
batchLoss += loss.data.item()
#
for iLayer in range(nLayer):
allLayers[iLayer].update(learning_rate/nBatch)
#
if (iEpoch%(nEpoch//10)==0): # dump model occasionaly
dumpLoad("allLayers.dump", whatToDo="dump", myObject=allLayers)
print(f'{iEpoch:5d} {batchLoss/nBatch:8.4f}')
#
# generate text, token per token, greedy
#
inLetters = trainingText[0:nContext]
inActivity = torch.zeros(nContext,dim,device=myDevice)
for iC in range(nContext):
inActivity[iC] = letterEmbedding[inLetters[iC]]
print('.'.join(inLetters), end="")
#
nGen = 0
while (nGen<20):
nGen += 1
outActivity = model(inActivity)
lastOutToken = outActivity[nContext-1]
if (1==2):
print(inActivity)
print(outActivity)
print(lastOutToken.data)
#
bestChar = '@'
bestMatch = 1.0e12
for letter in vocabulary:
match = torch.square(lastOutToken-letterEmbedding[letter]).sum().data.item()
if (match<bestMatch):
bestMatch = match
bestChar = letter
print(f'_{bestChar:1s}', end="")
inLetters.append(bestChar)
inActivity = inActivity.roll(-1,0) # cyclic left shift
inActivity[nContext-1] = letterEmbedding[bestChar]
#
print()
print(''.join(inLetters), end="")
print()
if (1==2):
print(vocabulary)
print(letterEmbedding)
$$
\begin{array}{ccccccc}
\fbox{$\phantom{\big|}\mathrm{input}\phantom{\big|}$}
&\to&
\fbox{$\phantom{\big|}\mathrm{attention}\phantom{\big|}$}
&\to&
\fbox{$\phantom{\big|}\mathrm{normalization}\phantom{\big|}$}
& &
\\[0.5ex]
&\to&
\fbox{$\phantom{\big|}\mathrm{feed forward}\phantom{\big|}$}
&\to&
\fbox{$\phantom{\big|}\mathrm{normalization}\phantom{\big|}$}
&\to&
\fbox{$\phantom{\big|}\mathrm{output}\phantom{\big|}$}
\end{array}
$$
