Advanced Introduction to C++, Scientific Computing and Machine Learning
Claudius Gros, SS 2024
Institut for Theoretical Physics
Goethe-University Frankfurt a.M.
Neural Networks
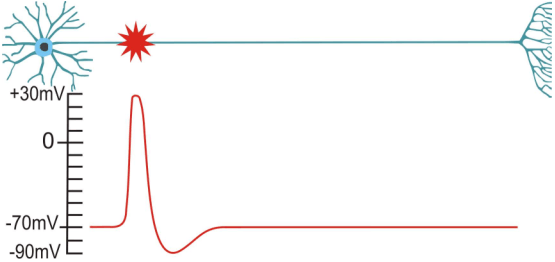
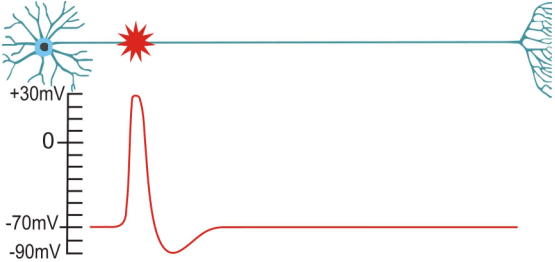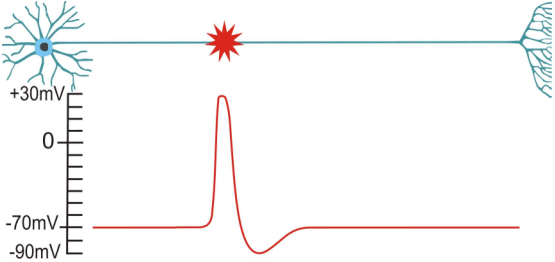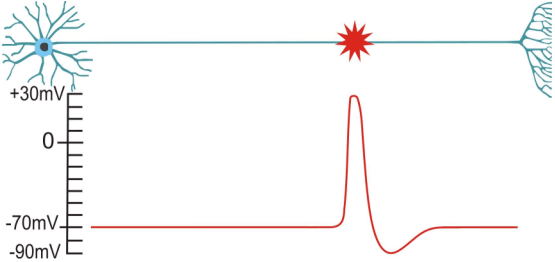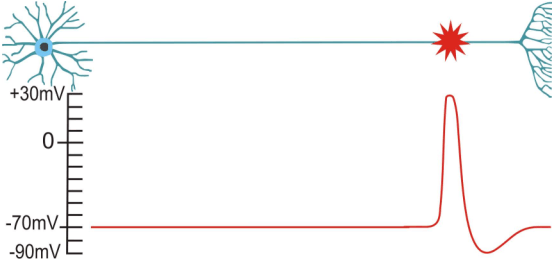
neurons in the brain
a brain full of neurons
- 80-100 billion
- 1000-10000 connections (synapse) per neuron
binary information transmission
- spike $\ \hat{=} \ $ electrical solitary wave
: action potential
synapses are chemical
- pre-synaptic spike $\ \ \to \ \ $ vesicles pop
- neurotransmitter $\ \to \ $ receptors
: glutamate (excitatory)
: GABA (inhibitory)
all constituent proteins recycled
(days, weeks), functional stationarity
artificial neurons
rate encoding
- neural activity $\ \ y_i\in[-1,1]$
$\hat{=} \ $ normalized number of spikes per time
$\qquad\quad
y_i = \sigma(x_i-b_i),\qquad\quad x_i=\sum_j w_{ij}y_j
$
- membrane potential $\ \ x_i$
- threshold $\ \ b_i$
- transfer function
$\qquad\qquad\qquad\quad \fbox{$\phantom{\big|}
y(z)=\tanh(z)\phantom{\big|}$}$
synaptic weights
- weighted connectivity matrix $\ \ w_{ij}$
: post-synaptic: $ \ \ i\ \leftarrow j \ \ $ pre-synaptic
- synaptic plasticity
: find optimal $\ \ w_{ij}$
: supervised / unsupervised
linear classifier
- hyperplane
$$
\fbox{$\phantom{\big|}
\sum_j w_{ij} y_j = b_i
\phantom{\big|}$}
\qquad\quad
\mathbf{w}\cdot\mathbf{y}=b
$$
in the space of pre-synaptic activities $ \ \ y_j$
: every neuron $\ \ i$
- soft classification $ \ \ y_i=\sigma(x_i-b_i)$
unsupervised learning
what fires together,
wires together

Hebbian learning
- unsupervised - no teacher
- extraction of statistical correlation
for the data input stream
- causality
$$
\frac{d}{dt} w_{ij} \sim y_i y_j
$$
linear model
$\qquad\quad
\fbox{$\phantom{\big|}
\left\langle \frac{d}{dt}
w_{ij}\right\rangle \sim
\sum_k w_{ik}\big\langle y_k y_j\big\rangle
\phantom{\big|}$}\,,
\qquad\quad
y_i\sim x_i = \sum_k w_{ik}y_k
$
- covariance matrix of inputs
$$
S_{kj} = \big\langle (y_k-\overline{y}_k) (y_j-\overline{y}_j)\big\rangle =
\big\langle y_k y_j\big\rangle,
\qquad\quad
\overline{y}_k\to0
$$
- generalizable for finite mean $ \ \ \overline{y}_k$
- limit growth via overall normalization $\ \ \sum_j w_{ij}^2\to\mbox{const.}$
principal compoment analysis
- Hebbian learning
$$
\left\langle \frac{d}{dt}
w_{ij}\right\rangle \sim
\sum_k w_{ik}S_{kj},
\qquad\quad
\fbox{$\phantom{\big|}\displaystyle
\tau_w\frac{d}{dt} \hat{w} = \hat{w}\cdot\hat{S}
\phantom{\big|}$}\,,
\qquad\quad
\big(\hat{w}\big)_{ij} = w_{ij}
$$
with
$$
\big(\hat{S}\big)_{kj} = \big\langle (y_k-\overline{y}_k) (y_j-\overline{y}_j)\big\rangle,
\qquad\quad
\sum_j w_{ij}^2\to\mbox{const.}
$$
competitive growth of components
- diagonalize input-covariance matrix $\ \ \hat{S}$
$$
\hat{S} = \sum_{\{\lambda\}} \lambda \,
\mathbf{e}_\lambda^{\phantom{T}} \mathbf{e}_\lambda^T,
\qquad\quad
\hat{S}\, \mathbf{e}_\gamma= \lambda\, \mathbf{e}_\gamma,
\qquad\quad
\mathbf{e}_\lambda\cdot\mathbf{e}_\gamma=
\mathbf{e}_\lambda^T\mathbf{e}_\gamma^{\phantom{T}} = \delta_{\lambda,\gamma}
\qquad\quad
$$
- growth of weight components
$$
\tau_w\frac{d}{dt}\big( \hat{w}\cdot\mathbf{e}_\gamma^{\phantom{T}}\big)
= \hat{w}\cdot\hat{S}\cdot\mathbf{e}_\gamma^{\phantom{T}}
= \sum_{\{\lambda\}}\lambda\, \hat{w}\cdot \mathbf{e}_\lambda^{\phantom{T}}
\underbrace{
\mathbf{e}_\lambda^T \cdot\mathbf{e}_\gamma^{\phantom{T}}
}_{\delta_{\lambda,\gamma}},
\qquad\quad
\fbox{$\phantom{\big|}\displaystyle
\tau_w\frac{d}{dt}\big( \hat{w}\cdot\mathbf{e}_\gamma^{\phantom{T}}\big)
= \gamma\,\big( \hat{w}\cdot\mathbf{e}_\gamma^{\phantom{T}}\big)
\phantom{\big|}$}
$$
- normalization $\ \ \to \ \ $ competive growth
- Hebbian learning finds the direction of the
covariance matrix with the largest eigenvector $\ \gamma\ $, the
principal component,
viz the input activities with the largest variance


neural networks
feed-forward
- organized in layers
$
\fbox{$\phantom{\big|}$ input $\phantom{\big|}$}
\quad\to\quad
\fbox{$\phantom{\big|}$ hidden $\phantom{\big|}$}
\quad\to\quad\dots\quad\to\quad
\fbox{$\phantom{\big|}$ output $\phantom{\big|}$}
$
$\hat{=}\ \ $ cortical layers (brain)
- directed flow of information
'hidden' means internal
- widespread use
recurrent
- closed dynamical system
- fixpoint attractor
- limit cycles
- chaotic attractors
if deterministic
- attractors may correspond to
- memories (fixpoints)
- motor primitive (limit cycles)
- ...
- behavior may be
- self-organized (emergent)
- learned
perceptron
- single layer
$
\fbox{$\phantom{\big|}$ input $\phantom{\big|}$}
\quad\to\quad
\fbox{$\phantom{\big|}$ output $\phantom{\big|}$}
$
input units (not 'input neurons')
supervised learning
- encode mapping input to ouput
$
\fbox{$\phantom{\big|}\displaystyle
\mathbf{I}_\alpha\ \to\ \mathbf{y}_\alpha
\phantom{\big|}$}\,,
\qquad\quad
\mathbf{y} = \mathbf{y}(\mathbf{x}_\alpha),
\qquad\quad
\mathbf{x}_\alpha = \hat{w}\cdot\mathbf{I}_\alpha
$
for a training pairs $\ (\mathbf{I}_\alpha,\mathbf{y}_\alpha)$, where
$
\mathbf{I}=\big(I_1,\,..,\,I_{N_0}\big),
\qquad\quad
\mathbf{y}=\big(y_1,\,..,\,y_{N_1}\big),
\qquad\quad
\big(\hat{w}\big)_{ij} = w_{ij}
$
- minimize
$$
\fbox{$\phantom{\big|}\displaystyle
E = \frac{1}{2}
\big|\mathbf{y}_\alpha-\mathbf{y}(\mathbf{x}_\alpha)\big|^2
\phantom{\big|}$}\,,
\qquad\quad
(\mathbf{y}(\mathbf{x}_\alpha))_i=\sigma\big((\mathbf{x}_\alpha)_i-b_i\big)
=\sigma\left(\sum_j w_{ij}(\mathbf{I}_\alpha)_j-b_i\right)
$$
transfer function $\ \ \sigma(z)$
steepest descent
- gradient for a single input-ouput pair
$$
\frac{d}{dt}w_{ij} \sim
-\frac{\partial E}{\partial w_{ij}} =
\left[
(\mathbf{y}_\alpha)_i-(\mathbf{y})_i
\right]\,\sigma'(.)
\,(\mathbf{I}_\alpha)_j
$$
- learning stops when $ \ \ \mathbf{y}\to \mathbf{y}_\alpha$
- monotonic transfer function $\ \ \sigma'(.)>0$
the XOR problem
- single neurons are linear classifiers
- XOR not solvable via linear classification
the neural-network winter
- 1970' and 1980'
- universal computation needs XOR
$\Rightarrow\ \ $ (single-layer) neural networks not universal
- deep learning did not work
- problems too simple
- limited training data
- engineering
universality of multilayer perceptrons

supperpositions of linear functions
are still linear
- parametrized family of non-linear functions
$\qquad\quad
\begin{array}{rcl}
y_5 &=& \sigma(w_{5,3}y_3+w_{5,4}y_4) \\
&=& \sigma\Big(
w_{5,3}\sigma(w_{3,1}I_1+w_{3,2}I_2) \\
& & \phantom{\sigma}+ w_{5,4}\sigma(w_{4,1}I_1+w_{4,2}I_2)
\Big)
\end{array}
$
linear neurons
- case $\ \ y(x) = a x$
- additional layer do not improve performance
non-linear neurons
- output may be a ridge if
$
w_{3,2}=-w_{3,1}, \qquad\quad w_{4,2}=-w_{4,1},
\qquad\quad b_3\ne b_4$


- 4 hidden-layer neurons representing
two orthognal ridges make a bump
- bumps are universal
given enough hidden layer neurons, non-linear
neurons can represent any smooth function
derivative of sigmoidal
- here $\ \ y_i\in[0,1]$
$\qquad\quad
y_i = \sigma(x_i-b_i),
\qquad\quad
\sigma(z) =\frac{1}{1+\mathrm{e}^{-z}}
$
- derivative of sigmoidal
$\qquad\quad
\frac{d\sigma}{dz} =
\frac{\mathrm{e}^{-z}}{(1+\mathrm{e}^{-z})^2}
=\sigma^2(1/\sigma-1)
$
viz
$$\fbox{$\phantom{\big|}\displaystyle
\sigma' = \sigma(1-\sigma) \phantom{\big|}$}\,,
\qquad\quad
\frac{d}{dx} y_i= y_i(1-y_i)
$$
backpropagation
- layers $\ \ i,\,j,\, k\,\,\dots$
$
x_i = \sum_j w_{ij} y_j = \sum_j w_{ij} \sigma(x_j-b_j)
=\dots $
training multilayer perceptrons
$\qquad\quad
\frac{\partial y_i}{\partial w_{\alpha\beta}}
= y_i(1-y_i)\sum_j w_{ij} \frac{\partial y_j}{\partial w_{\alpha\beta}}
$
- layer indices $\ \ \alpha,\beta $
- target value $ \ \ \tilde{y}_i$
- gradient of error function
$$
E=\frac{1}{2} \sum_i\big(y_i-\tilde{y}_i\big)^2,
\qquad\quad
\frac{\partial E}{\partial w_{\alpha\beta}} =
\sum_i \big(y_i-\tilde{y}_i\big) \frac{\partial y_i}{\partial w_{\alpha\beta}}
$$
viz
$$
\fbox{$\phantom{\big|}\displaystyle
\frac{\partial E}{\partial w_{\alpha\beta}} =
\sum_i \Delta E_i \frac{\partial y_i}{\partial w_{\alpha\beta}}
\phantom{\big|}$}\,,
\qquad\quad
\Delta E_i=y_i-\tilde{y}_i
$$
with the intial error $\ \ \Delta E_i$
recursive derivatives
$$
\frac{\partial E}{\partial w_{\alpha\beta}}
= \sum_i\big(y_i-\tilde{y}_i\big)\,
y_i(1-y_i)\sum_j w_{ij} \frac{\partial y_j}{\partial w_{\alpha\beta}}
$$
$\quad\quad$ and hence
$$
\frac{\partial E}{\partial w_{\alpha\beta}}
= \sum_j \Delta E_j \frac{\partial y_j}{\partial w_{\alpha\beta}},
\quad\qquad
\fbox{$\phantom{\big|}\displaystyle
\Delta E_j = \sum_i\Delta E_i\, y_i(1-y_i)\, w_{ij}
\phantom{\big|}$}
$$
- back-propagated error $ \ \ \Delta E_j$
- note: $\ \ y_i(1-y_i)>0$
: may be omitted
supervised learning via gradient descent is
equivalent to linear backpropagation of errors
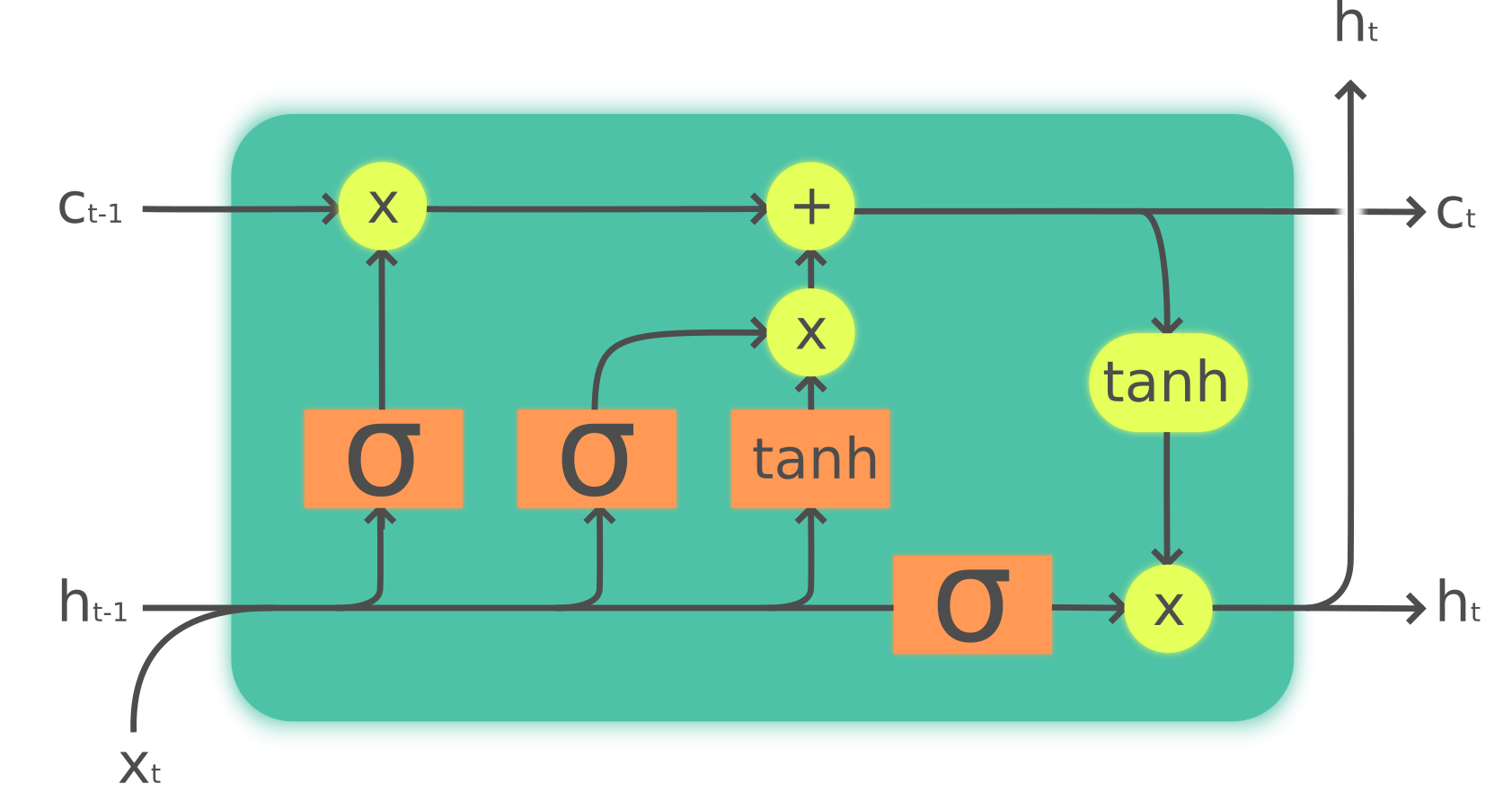
long short-term memory
neurons with interal states
- $h_{t-1}\,$:: input from previous layer
- $c_{t-1}\,$:: internal state (memory) at the start of time step
- $x_{t\phantom{-1}}\,$:: external input
internal state manipulation
- forget/update $\ \Rightarrow\ $ new internal state $c_t$
- output to next layer: $\ h_t$
:: nonlinear weighted superpostion of
$\ \ x_t$, $h_{t-1}$, $c_t$
- all operations learned (weights adapted)