variational inference

conditional probabilities

• $\mathcal{D}\ $ : dataset with elements $(\mathbf{x},\mathbf{y})$,
  $\mathbf{x}\ $ : input
  $\mathbf{y}\ $ : output
• $\mathbf{w}\ $ : network parameters (weights)
• $P(\mathcal{D}|\mathbf{w})\ $ : conditional probability for data $\mathcal{D}$, for a given configuration of $\mathbf{w}$
  :: both $\mathbf{x}$ and $\mathbf{y}$ are given for supervised learning

accuracy objective

• $L^N(\mathbf{w},\mathcal{D})\ $ : network loss function

$$ L^N(\mathbf{w},\mathcal{D}) = -\log\big(P(\mathcal{D}|\mathbf{w})\big) = - \sum_{(\mathbf{x},\mathbf{y})\in\mathcal{D}} \log\big(P(\mathbf{y}|\mathbf{x},\mathbf{w})\big) $$

• is minimal if there is one $\mathbf{y}$ for every $\mathbf{x}$
  :: entropy is positive definite, vanishing in the absence of noise

variational inference

• $P(\mathbf{w}|\alpha)\ $ : prior distribution of weights (before training), depending on parameter $\alpha$
• $P(\mathbf{w}|\mathcal{D},\alpha)\ $ : posterior weight distribution (given training data $\mathcal{D}$)
  :: not tractable
• $P(\mathbf{w}|\mathcal{D},\alpha)$ is approximated by
  $Q(\mathbf{w}|\beta)$, determined variationally, viz by minimizing a given objective function
• $\mathcal{F}\ $ : variational free energy

$$ \mathcal{F} = - \left\langle \log\left[ \frac{P(\mathcal{D}|\mathbf{w})P(\mathbf{w}|\alpha)}{Q(\mathbf{w}|\beta)} \right]\right\rangle_{\mathbf{w}\sim Q(\beta)} $$

Kullback Leibler divergence

$$ \mathcal{F} = \left\langle L^N(\mathbf{w},\mathcal{D}) \right\rangle_{\mathbf{w}\sim Q(\beta)} + D_{\rm KL}\big(Q(\beta)\parallel P(\alpha)\big) $$

• $\langle L^N(\mathbf{w},\mathcal{D}) \rangle_{\mathbf{w}\sim Q(\beta)}\ $ : parametrized by $Q(\beta)$, instead of $\mathbf{w}$
• $D_{\rm KL}(Q(\beta)\parallel P(\alpha)) \ $ : Kullback-Liebler divergence ('distance')
  :: positive definite
  :: $D_{\rm KL}\equiv 0\ $ if and only if $Q(\beta)$ and $P(\alpha)$ identical
  :: converged if posterior $\equiv$ prior

variational distributions

• minimization procedure possible for a given parametrization of $Q(\mathbf{w},\beta)$
• Gaussian: mean $\mu_i$ and standard deviation $\sigma_i$ for parameter $w_i$
• same parametrization for prior $P(\mathbf{w}|\alpha)$

inference

• result is a distribution, parametrized by $(\mu_i,\sigma_i)$,
  for network parameters: not a single value
• set of $(\mu_i,\sigma_i)$ updated with every new observation,
  :: viz with every new data $(\mathbf{x},\mathbf{y})$
  :: inference: updating of a distribution with new observations
• next step: start posterior as new prior
  :: $(\mu_i,\sigma_i)$ are now the parameters of the prior

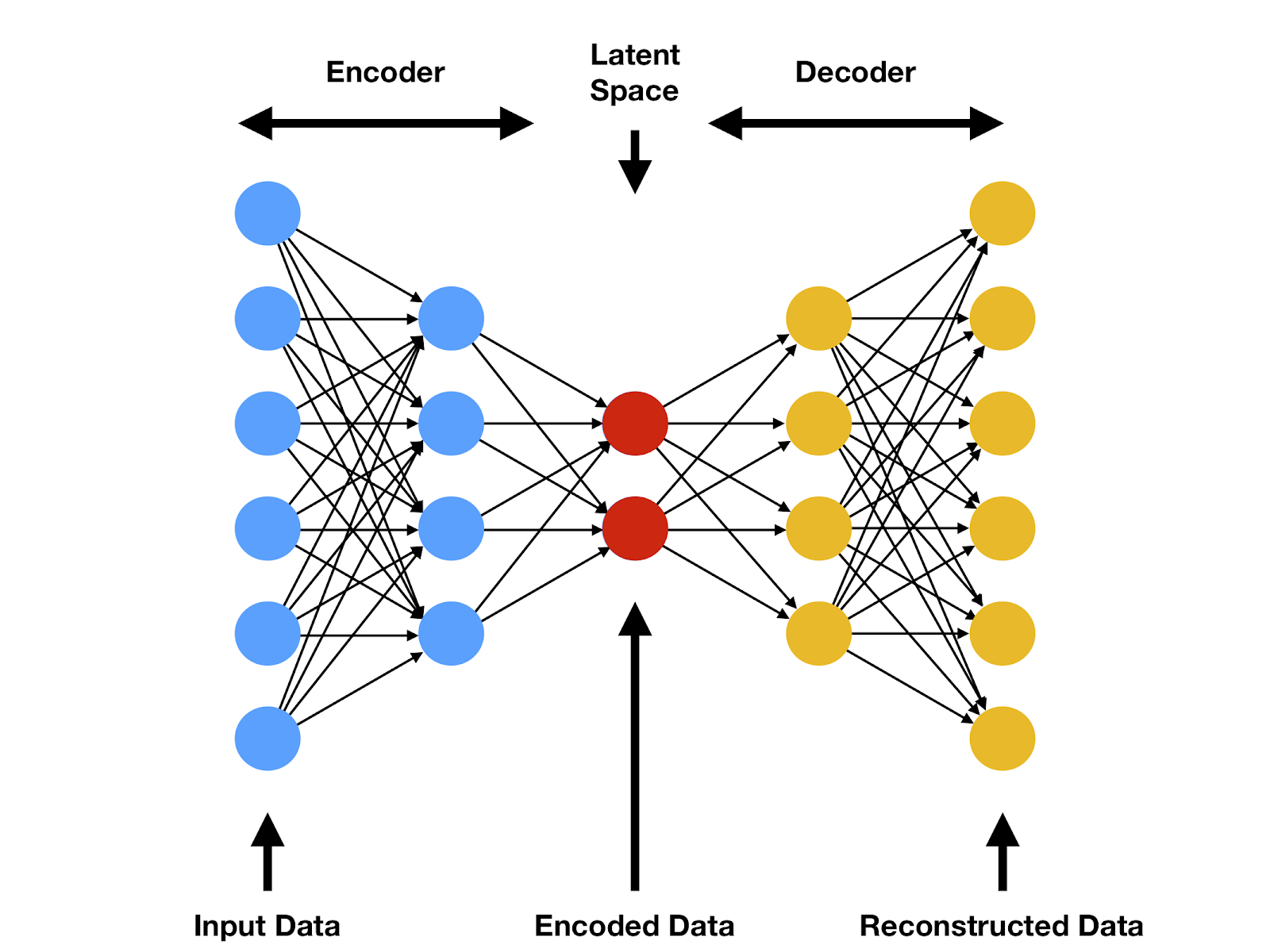
variational autoencoder

• latent space ('encoded space')
  
  • for normal autoencoder
    :: not structured, just a bottleneck
  • for variational autoencoder
    :: maximal information
• maximize information when encoding
• minimized reconstruction error when decoding
• $\mathbf{x}\ $ : input
  $\mathbf{z}\ $ : latent state
  $\mathbf{y}\ $ : output

probabilistic network representations

• $Q(\mathbf{w}|\beta)\ $ : encoder
  $Q^\prime(\mathbf{w}^\prime|\beta^\prime)\ $ : decoder
  :: probabilities to generated networks parameters $\mathbf{w}\,/\,\mathbf{w}^\prime$
  :: encoded by variational parameters $\beta\,/\,\beta^\prime$ (Gaussians)

accuracy target

• $P(\mathbf{y}|\mathbf{z},\mathbf{w}^\prime)\ $ : probability to find $\mathbf{y}$ for given $\mathbf{z}$ and $\mathbf{w}^\prime$

$$ \mathcal{F}_{\mathrm{accuracy}} = - \sum_{(\mathbf{x},\mathbf{y})\in\mathcal{D}} \log\big(P(\mathbf{y}|\mathbf{z},\mathbf{w}^\prime)\big) $$

• $\mathbf{y}\hat{=}\mathbf{x}\ $ for autoencoder
• minimal if there is an $\mathbf{y}$ for every $\mathbf{z}$

information maximization

• variational inference between input and latent space
• posterior and prior (both variational)

$$ \mathcal{F}_{\mathrm{information}} = D_{\mathrm{KL}} \big(P_{\mathrm{posterior}} \parallel P_{\mathrm{prior}} \big) $$

• with

$$ P_{\mathrm{prior/posterior}} = P(\mathbf{z}|\mathbf{x},\mathbf{w})\Big|_{\mathrm{before/after\ updating}} $$

natural language processing (NLP)

encoder-decoder architectures for NLP

• encoder
  every layer receives an input
  $ \mathbf{h}_{t} = \mathbf{f}(\mathbf{h}_{t-1}, \mathbf{x}_t) $
  $\mathbf{h}_{t}\ $ : hidden layer state
  $\mathbf{x}_{t}\ $ : input (embedded words)
• decoder
  every layer makes a prediction,
  receiving previous predictions as input
  $ \mathbf{s}_{t} = \mathbf{g}(\mathbf{s}_{t-1}, \mathbf{y}_{t-1}) $
  $\mathbf{s}_{t}\ $ : hidden layer state
  $\mathbf{y}_{t}\ $ : predicted word (linear classifier, softmax)

word embedding

• preprocessing: word $\to$ vector
• consider inter-word correlations
  :: related words are closer in vector space
• example: Google Word2vec

variants

• apply to
  • variational encoders, decoders, and/or
  • recurrent neural networks (RNN)
  • normal units / long short-term units
• state-of-the-art until 2014-2017

semantic correlations

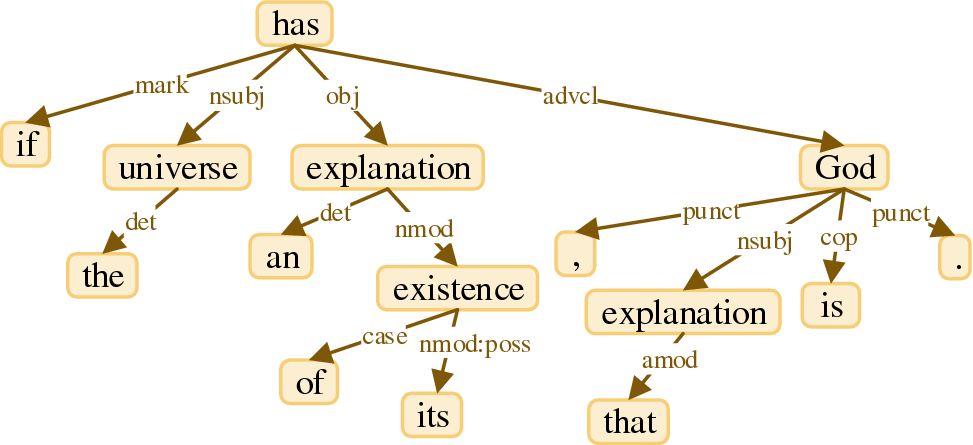
• posibly long-distance semantic correlations
  • classical approach: memory (fading)
  • state-of-the-art: attention

query, key & value

• $\sim0.75$ word -- tokens
  $\sim 5\cdot10^4$:   vocabulary size
• activity $\ \mathbf{x}$: current state
• three matrices (entries adapted via backpropagation)
  $\hat{Q}\ $: query
  $\hat{K}\ $: key
  $\hat{V}\ $: value
• $\mathbf{Q}$, $\mathbf{K}$, $\mathbf{V}$ vectors

$$ \mathbf{Q} = \hat{Q}\cdot\mathbf{x},\qquad \mathbf{K} = \hat{K}\cdot\mathbf{x},\qquad \mathbf{V} = \hat{V}\cdot\mathbf{x},\qquad $$

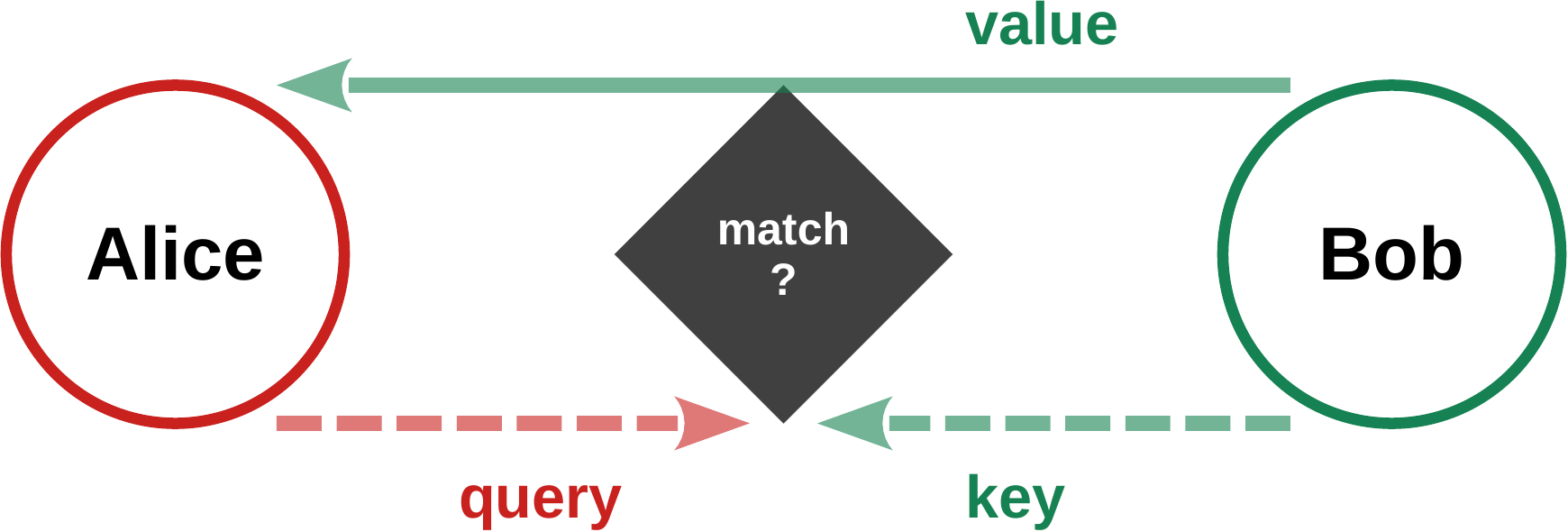
Alice: should I pay attention to Bob?

• databank query formalism
  
  • Alice sends its query $\ \mathbf{Q}_A\ $ to Bob
  • Bob compares $\ \mathbf{Q}_A\ $ with its key $\ \mathbf{K}_B$
  • if there is a match, sends back its value $\ \mathbf{V}_B$
• content-based attention via similarity
• self attention: between words of a sentence

dot-product attention

• scanning keys for similarity with query
  $\mathbf{K}_j \ $ : key of object
  $\mathbf{V}_j \ $ : value of object
  $\mathbf{Q}_{\phantom{j}} \ $ : query
  

$$ \mathbf{a} = \sum_j \alpha_j\mathbf{V}_j, \quad\qquad \alpha_{j} = \frac{\mathrm{e}^{e_{j}}}{\sum_i\mathrm{e}^{e_{i}}} \quad\qquad e_{j} = \mathbf{Q}\cdot\mathbf{K}_{j} $$

• $\mathbf{a}\ $ : attention vector
  :: activity of query token
  :: output of attention layer
• softmax (Boltzman distribution) superposition of values
• similarity: scalar product

[Bahdanau, Cho, Bengio 2014]

transformer block

$$ \begin{array}{ccccccc} \fbox{$\phantom{\big|}\mathrm{input}\phantom{\big|}$} &\to& \fbox{$\phantom{\big|}\mathrm{attention}\phantom{\big|}$} &\to& \fbox{$\phantom{\big|}\mathrm{normalization}\phantom{\big|}$} & & \\[0.5ex] &\to& \fbox{$\phantom{\big|}\mathrm{feed forward}\phantom{\big|}$} &\to& \fbox{$\phantom{\big|}\mathrm{normalization}\phantom{\big|}$} &\to& \fbox{$\phantom{\big|}\mathrm{output}\phantom{\big|}$} \end{array} $$

• input sentence
  :: embedded sequence of words (tokens)
• residual connections around attention layer are essential
• MLP: linear feedword layer:
• output of block $\ \equiv\ $ input of next block

multi-headed attention

• $h\ $ attention blocks in parallel ($h=8$)
  :: every token generates $\ h \ $ Q/K/V matrices
• allows for context specific attention

skip connections

skip/residual connections

• add identity in parallel to hidden layer
  $\mathbf{Layer}(\mathbf{x}) \ \to \ \mathbf{x}+\mathbf{Layer}(\mathbf{x})$
• additional normalization (transformer model)
  $\mathbf{Norm}\Big(\mathbf{x}+\mathbf{Layer}(\mathbf{x})\Big)$

advantages

• helps with vanishing gradient problem
  when backprogating learning signals
  during the training of deep networks
• if layer is superfluous, training can ignore it
• allows to add (self-) attention layers (transformer model)

positional encoding

• NLP before transformer (2017)
  :: read word by word
  :: encoder / decoder with RNN and LTSM
• NLP with transformer
  :: reading sentence by sentence
  :: no RNN, no LTSM; good for parallelization, GPUs
  :: uses self-attention with positional encoding

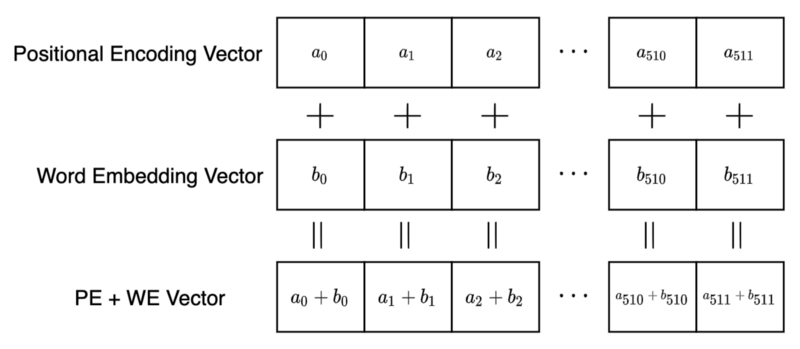
position of words in a sentence

• system needs position information when
  reading entire sentences at once
• for every word:
  $\mathbf{P}_e\ $ : positional encoding vector
  $\mathbf{W}_e\ $ : word embedding vector
• transformer architecture
  $\mathbf{P}_e$ and $\mathbf{W}_e$ have identical dimension
  $d_{\mathrm{model}}=512 \ $ : model dimension
• encoder input:
  $\mathbf{P}_e + \mathbf{W}_e\ $ : vector sum (times number of words)

discrete fourier analysis

• many types of positional encodings possible
  transfomer uses fourier components
• $L_s\ $ : length of input sentence
  $k\ $ : word position
  $d_{\rm model}\ $ : embedding dimension
  $i\in[0,d_{\rm model}/2]\ $ : encoding the embedding index

$$ P_e(k,2i ) = \sin\left(\frac{k}{K^{2i}}\right), \quad\qquad P_e(k,2i+1) = \cos\left(\frac{k}{K^{2i}}\right), \quad\qquad K = n^{1/d_{\mathrm{model}}} $$

• for $d_{\rm model}=512$ (transformer), one has a geometric series of
  $d_{\rm model}/2=256\ $ wavevectors $\ K^{2i}=1,\dots,n$
• $n=10^4\ $ (transformer)
• for the $k$th word, $P_e(k,j)$ is the $j$th entry
  of the positional embedding vector

recursive prediction

hello $\ \to\ $ hello

• own prediction $\ \equiv\ $ input (shifted by one token)

beam search

• the best output is

• run for the N mostly likely first words
• run for the N mostly likely two-word combinations
• ...

beam search

• large language models (LLMs) generate
  probabilities for output tokens
  :: words, syllables, letters
• greedy
  take token with highest probabilty
• chatGPT uses beam search

beam search

• classical search algorithm for probalistic trees
• N=2: width of search beam
• first position:
  select the N tokes with highest probabilities: A and C
• rerun system N times, with first position fixed
  :: generate new probabilities for second position
• evaluate combined probalities $\ \ p_{AX}$, $\ \ p_{CX}$
  for all second-position tokens $\ X$
• select N highest 2-token combinations: AB and CE
• rerun N times with fixed first/second positions
• ... repeat

combined probabilities

• position of output token: time step
• left (greedy)
  $0.5\cdot0.4\cdot0.4\cdot0.6=0.048$
• right (non-greedy second position)
  $0.5\cdot0.3\cdot0.6\cdot0.6=0.054$
• changed probabilities due to rerun

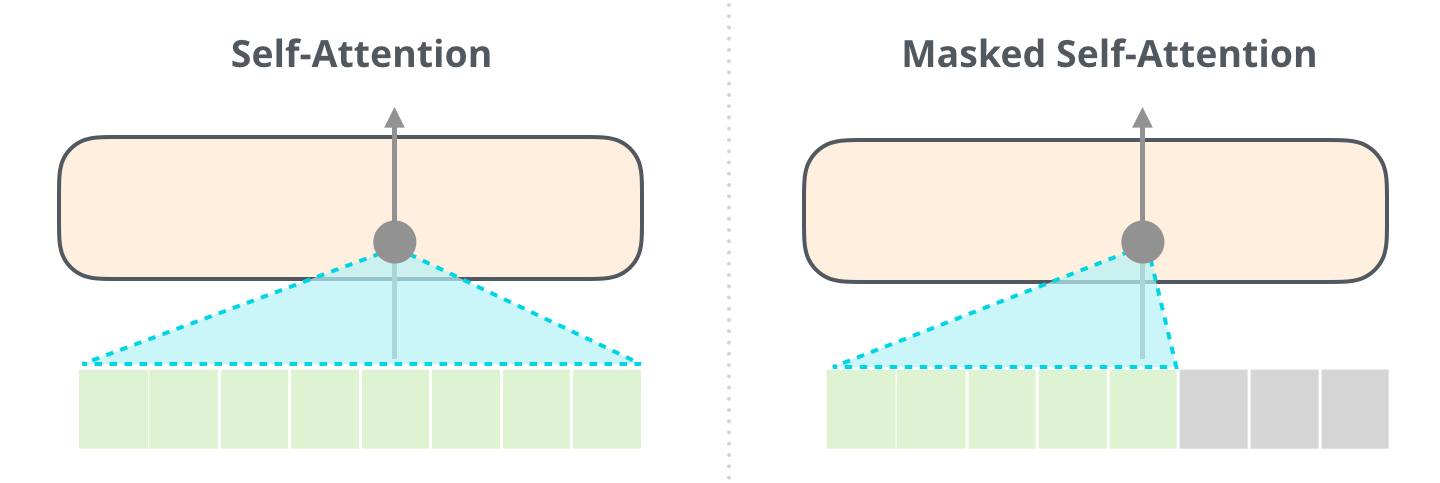
masked self attention

ordered input tokes

• attention to the left only (causality)
• value, key, query
  $ \mathbf{V}_m = \hat{V}_m \cdot \mathbf{x}_m, \qquad \mathbf{K}_m = \hat{K}_m \cdot \mathbf{x}_m $
  $ \mathbf{Q}_m = \hat{Q}_m \cdot \mathbf{x}_m $

• linearized attention
  [Linear Transformers]

$$ \begin{array}{rcl} \mathbf{s}_q^{\mathrm{(head)}} &= & \sum_k \mathbf{V}_k\, \mathrm{softmax}\Big(F_a(\mathbf{K}_k,\mathbf{Q}_{q})\Big) \\[0.5ex] &\to& \frac{\sum_k\mathbf{V}_k \big(\mathbf{K}_k\,\cdot\,\mathbf{Q}_{q}\big)} {\sum_k \mathbf{K}_k\,\cdot\,\mathbf{Q}_{q}} = \frac{\big(\sum_k \mathbf{V}_k \otimes\mathbf{K}_k\big)\,\cdot\,\mathbf{Q}_{q}} {\big(\sum_k \mathbf{K}_k\big)\,\cdot\,\mathbf{Q}_{q}} \end{array} $$

• outer product: $\ \otimes$
• additionally: positiveness

associative soft weight computing

• enters linearized attention (mean-field approximation)
  :: $\ W_{\rm tot}=\sum_k \mathbf{V}_k \otimes\mathbf{K}_k$

$$ W_m = W_{m-1} + \mathbf{V}_m \otimes\mathbf{K}_m $$

• akin to time decomposition of a autoassociative recurrent net
  :: internal state: $\ W_m$
• key-value associations

$$ \mathbf{V}_m \otimes\mathbf{K}_m = \mathbf{x}_m\,\cdot\,\big(\hat{V}_m \otimes\hat{K}_m \big)\,\cdot\,\mathbf{x_m} $$

why does it work?

attention in neuroscience / psychology

• external (saliency, 'something fast')
• top-down attention commands
  :: 'looking for a red object'
  $\color{brown}\Rightarrow \ $ humunculus problem
• “No one knows what attention is”   [Hommel et al., 2019]

ML attention

• Q, K, V matrices adapt to Q-K matching condition
  :: dot product
• attention $\ \color{brown}\equiv\ $ information routing
  :: self-optimized information bootleneck

• statistical learning of causal relations
  :: not (only) of information

foundation models

GPT - generative pretrained transformer

• number of adaptable parameters (matrix elements)
  :: $10^8$ / $10^9$ / $10^{11}$ / $10^{12}$
  :: GPT 1 / 2 / 3 / 4
• $10^3-10^4\ $ context tokens, $\ \sim 80\ $ layers

• SFT: $\ 10^4\!-\!10^5\ $ hand-crafted (prompt, response) pairs
  :: learns to answer; ¬(text completion)

applications / tasks on top of foundation model

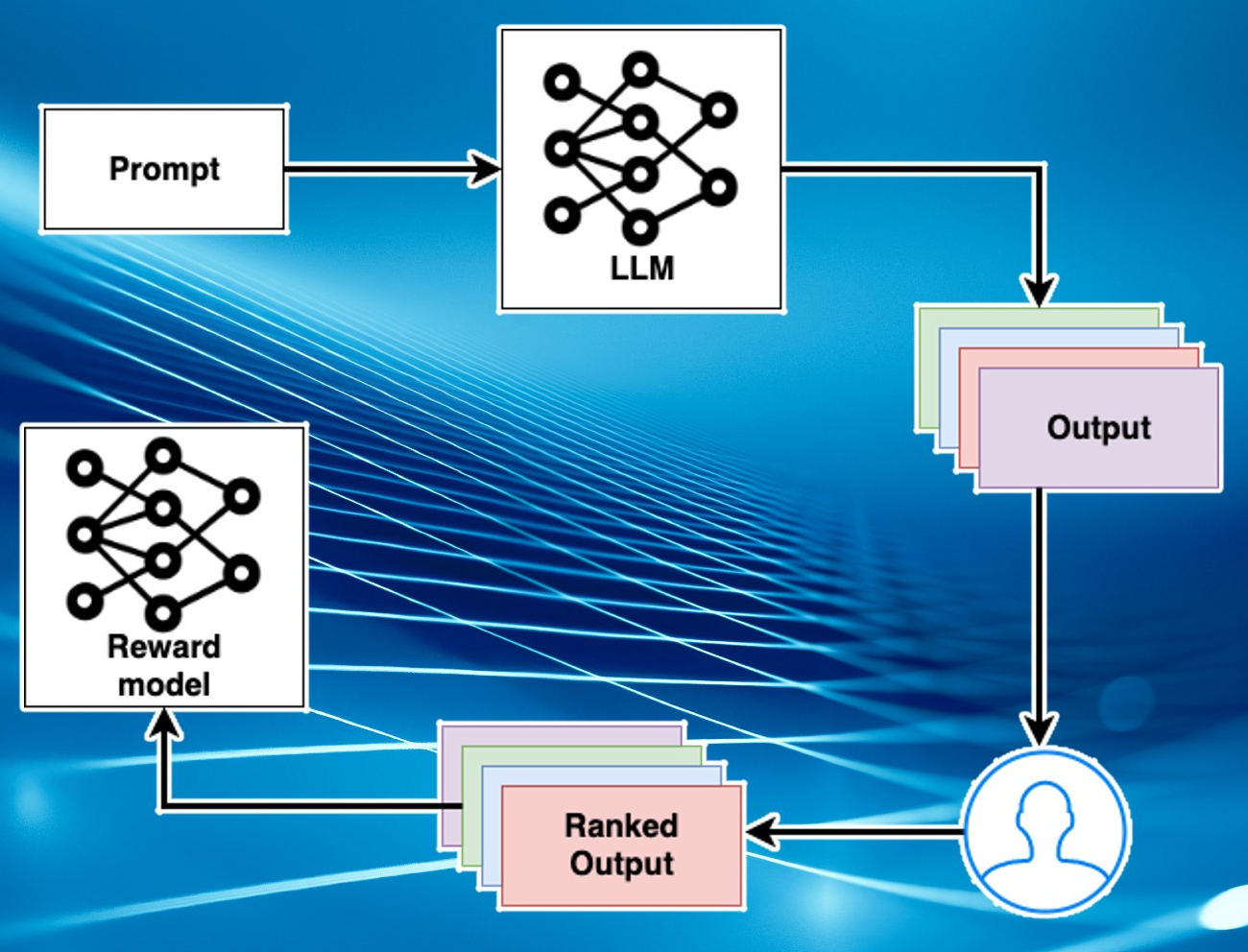
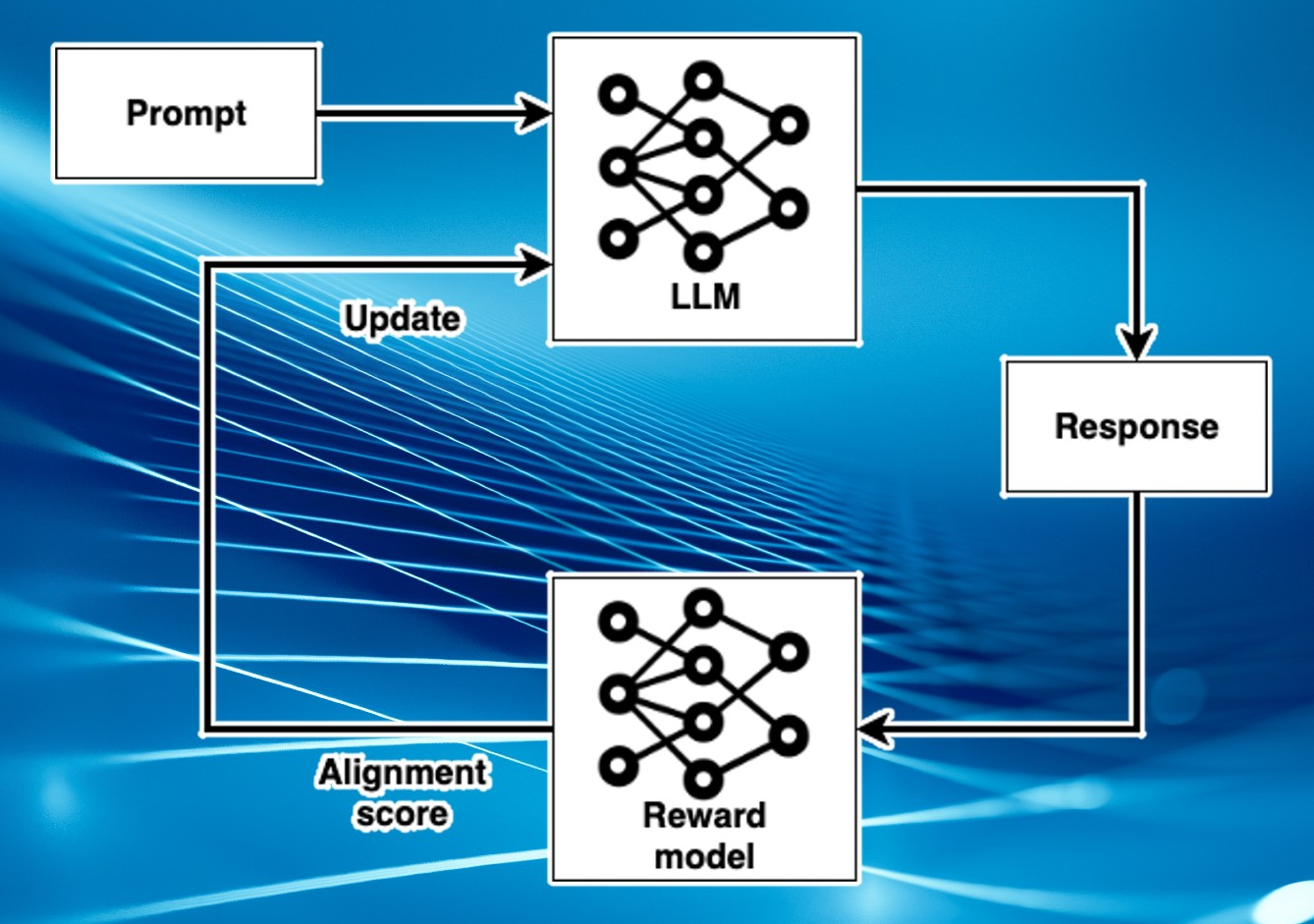
value alignment

reinforcement learning from human feedback (RLHF)

• reinforcement learning
  :: learning from feedback
• humans train the reward model
  the reward model trains GPT
  :: circumvents behavioral cloning
  $\color{brown}\Rightarrow\ $ value alignment
  $\color{brown}\Rightarrow\ $ ChatGPT

open-source explosion

LLaMA (Meta AI)

• public release Feb 2023
  :: 7B, 13B, 33B, and 65B parameters
  :: parameters leaked within a week

'We have no moat'

• leaked Google memo, May 2023

AI psychology

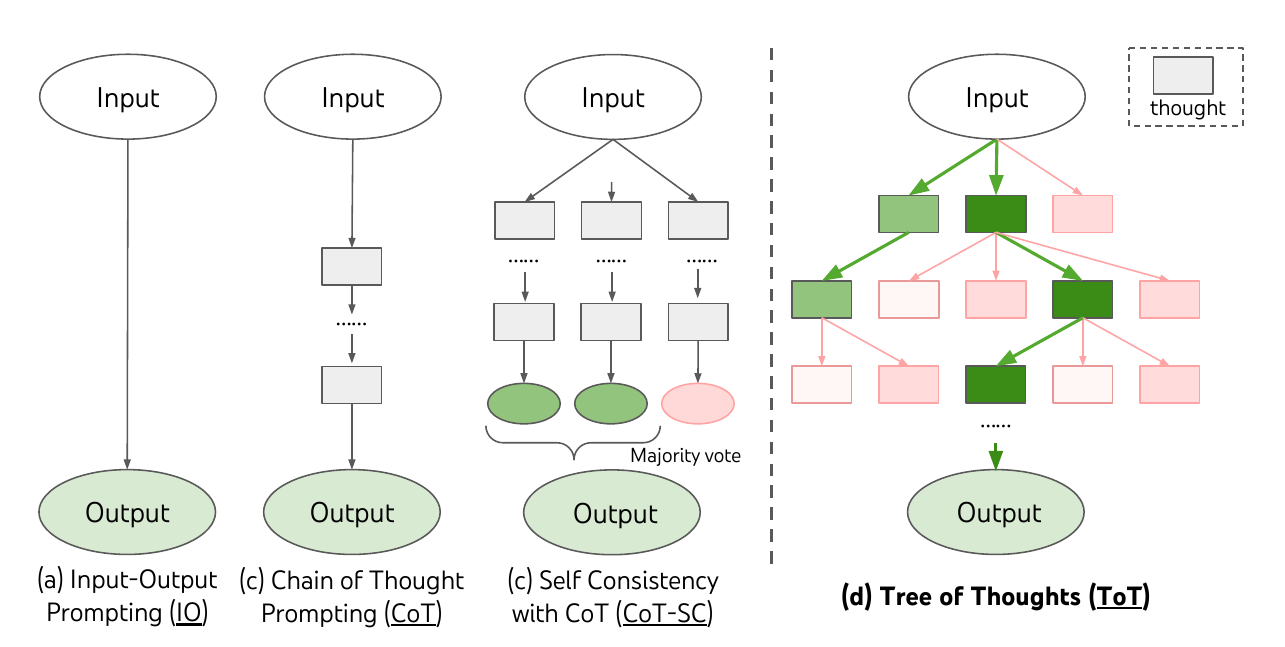
[Yao et.al, 2023]

Tree of Thoughts:
Deliberate Problem Solving with Large Language Models

• helping large language models to 'think'
  :: substantial performance boost

potential problems

value alignment

• democratic / liberal for most western chatBots
  :: no opinion given
• possible alternative value alignments
  :: socialist / suppressive (China)
  :: religious, e.g. islamic
  :: ...

copyright

• training corpus
• ¬(generated text)

social media polution

• mass generation of social media posts
  :: value marketing
  $\to\ \ $ training data polution

regulation

• data privacy / age verification / risk of wrong answers (Italy)
• EU AI act (dangerous applications)
• however, open-source explosion
  :: regulation no possible?