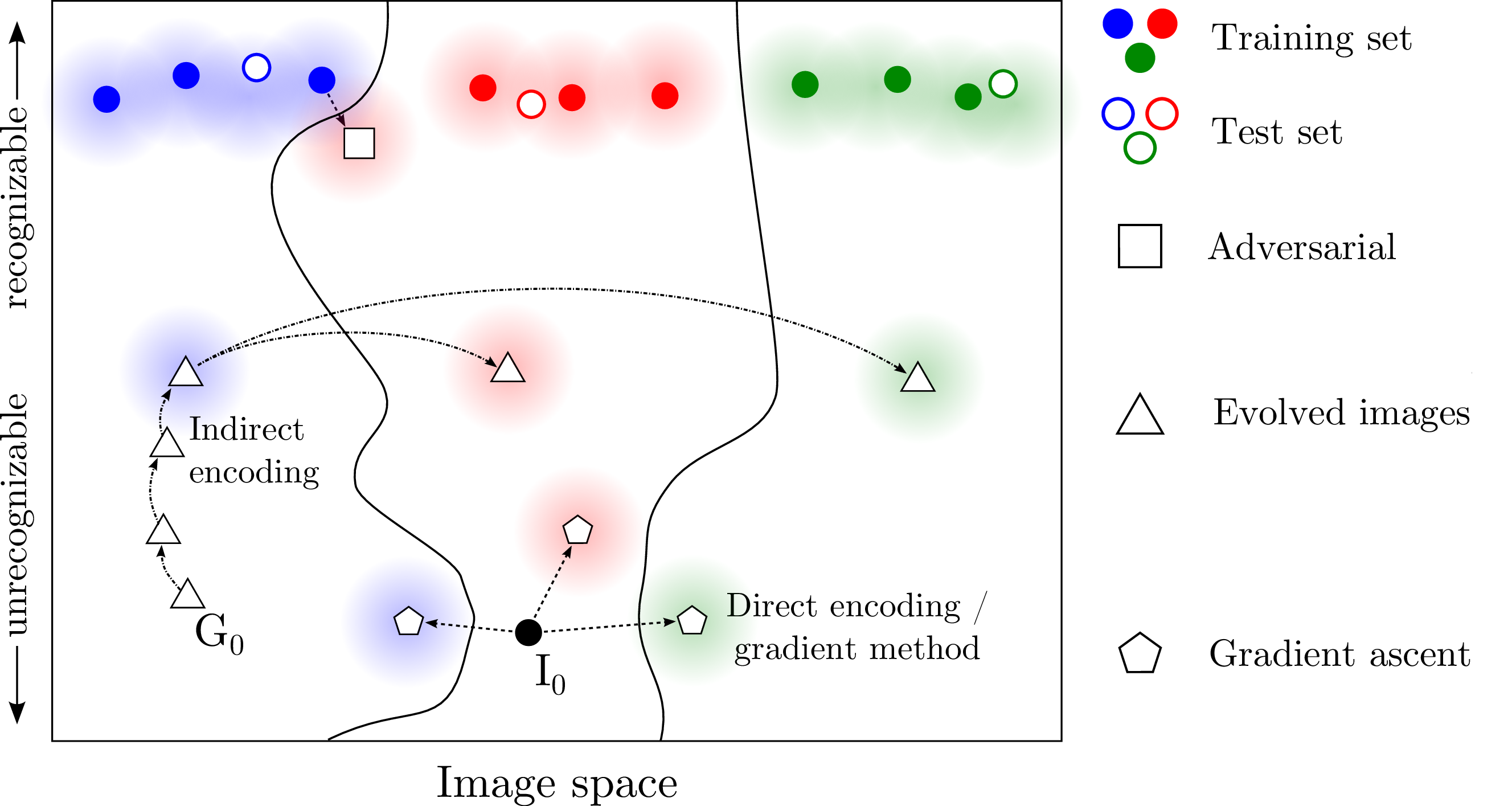
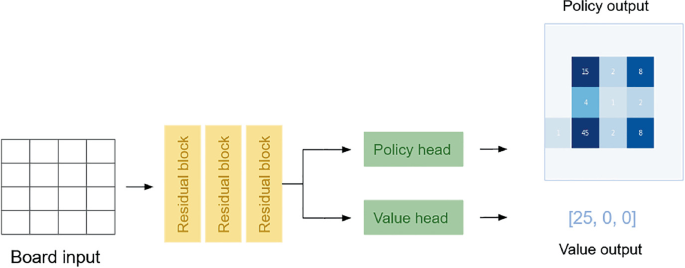
simple vs. complex problems
simple problems
- limited number of variables
- exact solution of interest, like for XOR
: lowest energy state
: gradient descent does not work
backpropagation fails for simple problems
complex problems
- large numbers of variables
- many 'good' local minima are ok
- humans would not survive, if it was otherwise
given enough (labeled) training data, large
classes of complex problems are 'solvable'
classes of complex problems are 'solvable'
- like playing Go, recognizing a face, ...
- counter-examples: cryptology, ...
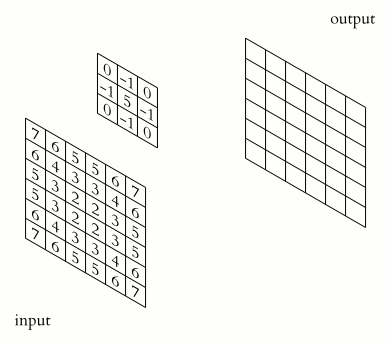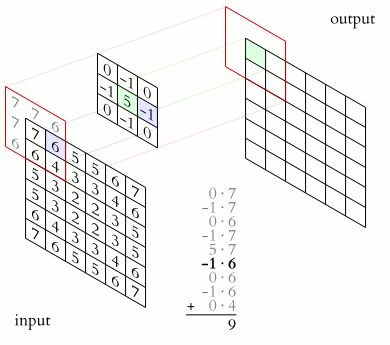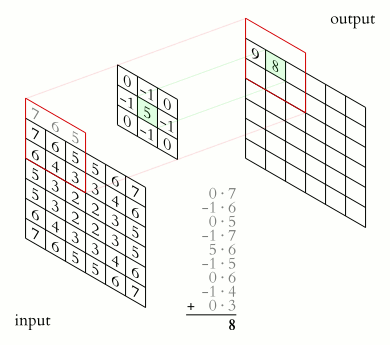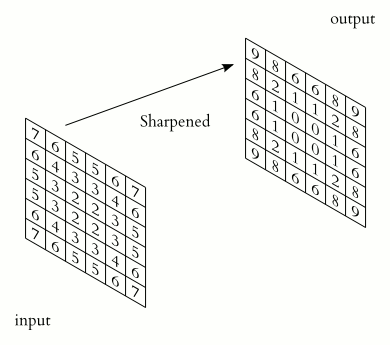
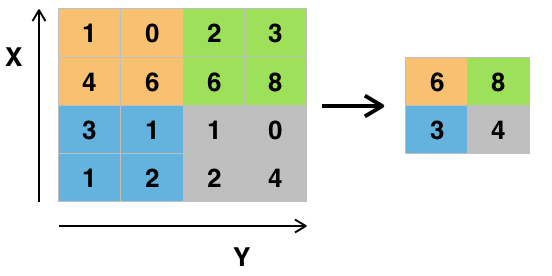 $\qquad$
$\qquad$