Advanced Introduction to C++, Scientific Computing and Machine Learning
Claudius Gros, WS 2021/22
Institut für theoretische Physik
Goethe-University Frankfurt a.M.
NM : Numerical Evaluation of Integrals
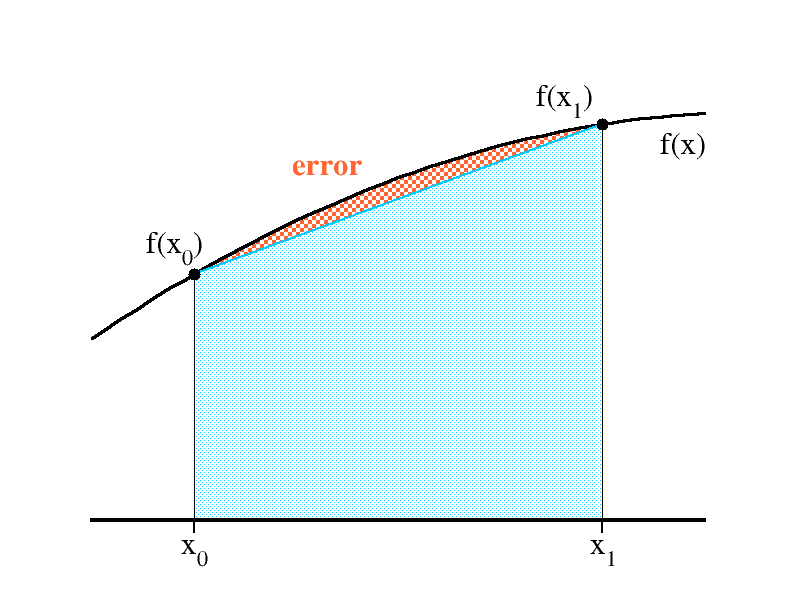
numerical integration
$$
I\ =\ \int_a^b\, f(x)\, dx
$$
$$
\int_{x_0}^{x_1} f(x)dx \ \approx\ \frac{f(x_0)+f(x_1)}{2}
\left(x_1-x_0\right)
$$
$$
T_n\ \equiv\
\sum_{k=1}^n\, \frac{f(x_{k-1})+f(x_{k})}{2}\,\Delta x
$$
trapezoidal rule at work
$$ y_m\ =\ \int_0^1\,
\frac{x^m}{x+a}\, dx$$
n p T(p) (4T(p)-T(p-1)/3
1 0 0.0454545454545455
2 1 0.0227273635533981 0.0151516362530156
4 2 0.0114620139299330 0.0077068973887780
8 3 0.0066417103644638 0.0050349425093074
16 4 0.0051140844181988 0.0046048757694438
32 5 0.0047045044781142 0.0045679778314194
64 6 0.0046002267297100 0.0045654674802419
128 7 0.0045740370560200 0.0045653071647900
256 8 0.0045674820820493 0.0045652970907257
512 9 0.0045658428656951 0.0045652964602438
1024 10 0.0045654330320428 0.0045652964208253
2048 11 0.0045653305717818 0.0045652964183615
4096 12 0.0045653049566010 0.0045652964182075
8192 13 0.0045652985527986 0.0045652964181978
16384 14 0.0045652969518476 0.0045652964181972
^ ^
9 16
- inverse recursion ($a=10$, $m=19$):
$\quad 0.0045652964181972$
- convergence acceleration with
$$ T_p^* \ =\ \frac{1}{3}\,\Big(4\,T(p)-T(p-1)\Big)$$
for $n=2^p$. Why?
convergence scaling
- scaling of accuracy as
a function of effort
accuracy of trapezoidal approximation improves
quadratically with the number of trapezoids
$$
I \ =\ \int_a^b\, f(x)\, dx\ \approx\ T_n \,+\, O(n^{-2})
$$
$$
T_n\ =\ \frac{\Delta x}{2}\,\sum_{k=1}^n\,
\Big(f(x_{k-1})+f(x_{k})\Big),
\qquad \Delta x\,=\, \frac{b-a}{n}
$$
$$
\begin{array}{rcl}
f(x_0+\delta x) & =& f(x_0) + f'(x_0)\delta x + O\big(\delta x^2\big),
\qquad\quad (\mbox{general})
\\
f(x_1) & =& f(x_0) + f'(x_0)\Delta x + O\big(\Delta x^2\big),
\qquad\quad \Delta x = x_1-x_0
\end{array}
$$
$$
\begin{array}{rcl}
T_n^{(1)} & =& \frac{\Delta x}{2}\Big(f(x_0)+f(x_1)\Big)
\ =\ \frac{\Delta x}{2}\Big(f(x_0)+f(x_0)+f'(x_0)\Delta x +O\big(\Delta x^2\big)\Big)
\\ & =& f(x_0)\Delta x+f'(x_0)\frac{\Delta x^2}{2} +O\big(\Delta x^3\big)
\end{array}
$$
$$
\begin{array}{rcl}
I^{(1)} & =& \int_{x_0}^{x_1} f(x)dx \ =\
\int_{0}^{\Delta x}dx' \Big(f(x_0)+f'(x_0)x'+O\big((x')^2\big)\Big)
\\ & =& f(x_0)\Delta x+f'(x_0)\frac{\Delta x^2}{2} +O\big(\Delta x^3\big)
\end{array}
$$
- difference for a single term / cummulative
$$
I^{(1)}-T_n^{(1)} \ \propto\ \big(\Delta x\big)^3,
\qquad\quad
I-T_n \ \propto\ n\big(I^{(1)}-T_n^{(1)}\big)
\ \propto\ \big(\Delta x\big)^2,
\qquad\quad \Delta x \propto 1/n
$$
- further systematics leads to the
Euler–Maclaurin formula
convergence acceleration
- exploit scaling for performance improvements
$$
T_n\ =\ I \,+\,\frac{c}{n^2} \,+\, \,O(n^{-3}),\quad\qquad
T_{2n}\ =\ I \,+\,\frac{c}{4n^2} \,+\, \,O(n^{-3})
$$
$$
\frac{4}{3}T_{2n}-\frac{1}{3}T_{n} \ =\
\left(\frac{4}{3}-\frac{1}{3}\right)\, I \,+\,
\left(\frac{4}{3}\frac{1}{4}-\frac{1}{3}\right)\, \frac{c}{n^2}
\,+\, \,O(n^{-3})
$$
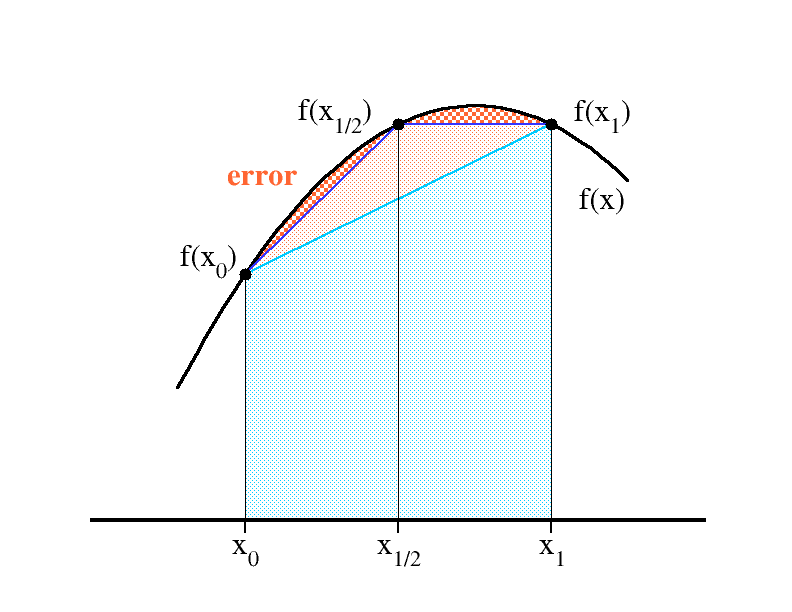
a single term
- from $\ S_n $ out of the interval $\ [x_0,x_1]$
$$
T_n\ \to\ \Delta x\frac{f_0+f_1}{2},\qquad\quad
T_{2n}\ \to\ \frac{\Delta x}{2}\Big(
\frac{f_0+f_{1/2}}{2}+\frac{f_{1/2}+f_1}{2}\Big)
,\qquad\quad
$$
$$
S_n\ \to\ \frac{\Delta x}{3}\Big(f_0+2f_{1/2}+f_1 -\frac{f_0+f_1}{2}\Big)
\ = \frac{\Delta x}{6}\Big(f_0+4f_{1/2}+f_1\Big)
$$
Simpson rule - error scaling
Compare
$$
S_n^{(1)}\ = \frac{\Delta x}{6}\Big(f_0+4f_{1/2}+f_1\Big),
\qquad\quad I^{(1)} \ =\ \int_{x_0}^{x_1} f(x) dx
$$
- Spimpson update
Using
$$
f(x_0+\delta x) \ =\ f(x_0) + f'(x_0)\delta x
+ \frac{1}{2}f''(x_0)\delta x^2
+ \frac{1}{6}f'''(x_0)\delta x^3
+ O\big(\delta x^4\big)
$$
we obtain $\quad f_0\ =\ f(x_0) \quad$ and
$$
f_{1/2}\ =\ f_0 + \frac{f'}{2}\Delta x + \frac{f''}{2\cdot4}\Delta x^2
+\frac{f'''}{6\cdot8}\Delta x^3,
\qquad\quad
f_{1}\ =\ f_0 + f'\Delta x + \frac{f''}{2}\Delta x^2 + \frac{f'''}{6}\Delta x^3
$$
and hence (with $1/6+1/12=1/4$)
$$
S_n^{(1)}\
= \frac{\Delta x}{6}\Big(6f_0+3f'\Delta x+f''\Delta x^2
+\frac{f'''}{4}\Delta x^3\Big)
$$
- integrating Taylor expansion
$$
I^{(1)} \ =\ \int_{0}^{\Delta x}dy\Big(
f_0 + f'y + \frac{1}{2}f''y^2 + \frac{1}{6}f'''y^3 \Big)
\ =\ f_0\Delta x +\frac{f'}{2}\Delta x^2
+\frac{f''}{6}\Delta x^3 +\frac{f'''}{24}\Delta x^4
$$
We hence find with
$$
I^{(1)}- S_n^{(1)} \ \propto\ O(\Delta x^5),\qquad\quad
I- S_n \ \propto\ O(\Delta x^4)
$$
that $\ S_n\ $ is accurate to $\ O(\Delta x^4)$, one order
more!
Romberg method
- general scaling
a series of approximations $\ A_n\ $ to $\ A\ $ (could be anything)
scales like
$$
A_n\ =\ A + \frac{c}{n^z},\qquad\quad
A_{2n} \ =\ A + \frac{1}{2^z}\frac{c}{n^z},\qquad\quad
aA_{2n}-bA_n\ =\ (a-b)A + \Big(\frac{a}{2^z}-b\Big)\frac{c}{n^z}
$$
- convergence accelerations
$$
B_{n} \ =\ aA_{2n}-bA_n, \qquad\quad
a \ =\ \frac{2^z}{2^z-1}, \qquad\quad
b \ =\ \frac{1}{2^z-1}, \qquad\quad
$$
Romberg iteration
$$
S_n \ =\ \frac{4}{3}T_{2n}-\frac{1}{3}T_{n} \ =\ I \,+\,O(n^{-4})
$$
accelerated integration
- simple to use, never hurts
- quadratic convergence acceleration
#include <iostream>
#include <stdio.h> // for printf
#include <math.h> // for pow
using namespace std;
/** Integrating
* y_m = \int_0^1 x^m/(x+a)dx
* for various m and n of the trapezoidal integration method
*/
// ---
// --- Straight summing up trapezoids
// ---
double sumTrapezoids(int n, int m, double a)
{
double result = 0.0;
double x0, x1;
double DeltaX = 1.0/n;
for (int i=0; i<n; i++)
{
x0 = i*DeltaX;
x1 = (i+1)*DeltaX;
result += 0.5*( pow(x0,1.0*m)/(x0+a) + pow(x1,1.0*m)/(x1+a) );
}
return result*DeltaX;
} // end of sumTrapezoids
// ---
// --- main
// ---
int main()
{
int m = 19;
double a = 10.0;
// *** ****************************** ***
// *** loop over numbers of trapzoids ***
// *** ****************************** ***
double Rn = 0.0;
double Sn = 0.0;
double lastSn = 0.0;
double Tn = 0.0;
double lastTn = 0.0;
int n = 1;
printf("%8s %5s %22s %22s %22s\n", "n","p","T(p)","(4T(p)-T(p-1)/3","(16S(p)-S(p-1)/15");
for (int jj=0; jj<15; jj++)
{
Tn = sumTrapezoids(n, m, a);
Sn = ( 4.0*Tn-lastTn)/3.0;
Rn = (16.0*Sn-lastSn)/15.0;
if (jj==0)
printf("%8d %5d %22.16f\n", n, jj, Tn);
if (jj==1)
printf("%8d %5d %22.16f %22.16f\n", n, jj, Tn, Sn);
if (jj>1)
printf("%8d %5d %22.16f %22.16f %22.16f\n", n, jj, Tn, Sn, Rn);
//
n = n*2;
lastTn = Tn;
lastSn = Sn;
}
printf("\n");
//
return 1;
}