Crowd Dynamics in Escape Situations

Introduction

One of the currently discussed topic of the dynamics of groups is the dynamic of crowds escaping some place in a competitive way. Even though this problem occurs repetitively in many critical social situations, the problem itself is rather rarely discussed in a basic scientific way.

The topic of crowd dynamics are somewhat related to the topics of swarm dynamics. The main difference shows in the basic behaviour of the group - where the agents of a swarm are interacting constructively, you will find the agents of a crowd just interacting in a very minimalistic way. Some panicking buffalos or people escaping a fire won't take notice of each other further than avoiding a total crash.

This LPZ Robots simulations tries to investigate the escape behaviour of such a crowd, wherein any agent has the same goal, and the influences of different intrinsic and extrinsic parameters on that behaviour.

Setup

This simulation contains several robots (50 for the most of the runs), which are instantiated inside a "room", that is a construct of five walls with only one door. The robots will try to leave the room by passing this door at the same time, so that they will crowd in front of this door. The observable parameters for all simulation series are the total execution time the whole group needs for escaping the room and in the same way the escape time for any individual robot.

The room the robots are escaping from is basically a square, where the front wall is replaced by two walls concurring with a certain angle at the door. The angle is chosen with 90 degrees for all simulations as it occurs not to have a large influence on the execution times. So we chose an angle with the minimal effect of robots sticking on the door frame. The doors broadness is a variable of this setup.

Within the room the robots begin the simulation arranged in a squared lattice. The lines of the lattice are displaced relative to the line in front with a small translation offset to have a better performance of the robots inside the room and get the crowdie behaviour just in the periphery of the door.

Roboter Setup

The robot is a basic model of the "Differential" type - so basically it is a cylinder shaped body with two wheels and a sensor bank with infrared sensors for obstacle avoidance.
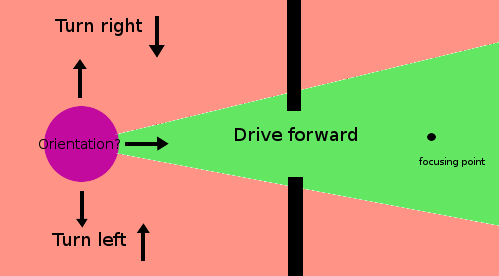
The basic type of this robot is modified with two additional sensors, as you can see below. One of those returns the absolute angular orientation of the robot, the other one measures the position of the robot related to a fixed point nearby the door.

Performance

The robots run with certain adjustable parameters. They have a mean velocity around which the individual velocities of the robots are distributed in a pseudorandom Gaussian way. Additional the number of robots joining the escape was adjustable, and so was the broadness of the gate as a geometric parameter.

The mean velocity is tested in a range from 2.5 velocity units to 20 velocity units in steps of 2.5. If not other mentioned, the mean velocity for testing series with other adjusted parameters is 5.
The standard deviation of the velocity distribution is tested in a range from 0 (exact velocity) to half the value of the mean velocity (so that the robots occupy velocity states between 0 and two times the mean velocity). If not other mentioned, the standard deviation for series not testing the deviation is 0.
The broadness of the gate is tested with space for 1 to 3.5 robots passing at once. If not other mentioned, 2.5 robots can pass the gate at once.

In every simulation run the sensor data is logged by every individual robot. The relative position sensor is used to determine the global time each robot leaves the room at and with this the time the last robot leaves the room at (which is the total execution time).

Results

The simulation was tested in several series for different parameters.

In steps of 10 the number of robots got changed between 20 and 100. The influence on the total execution time is rather trivial, but not very intuitive. We expected at least a power law correlation, since with a growing number of robots the crowding should increase rapidly. The result for the correlation was purely linear, as one can see in FIGURE 1. The flow of robots through the door seems not to be influenced by the degree and size of "crowdedness", but its pure existence seems to limit the flow of robots through the door.
The green line shows the "optimal flow" of the robots through the door with respect to the number - which is the flow the robots would leave the room with, when theo would totally ignore each other and walk out unimpeded. For large robot numbers this value is constant for the robots are starting in a squared lattice, which has a maximum distance to the door. If there are more robots than lattice spaces, the lattice spaces get filled more than once.

Second the broadness of the door was tested. In steps of 0.5 robot diameters (rd) the doors width was increased from 0 rd to 3.5 rd. At a first glance one would expect a monotonic hyperbolic decrease of the total execution time, relaxing for large widths of 7 rd (which is the squareside of the robots initializing geometry) and somewhat "diverging" for a door hardly wide enough for one robot.
The expectation is confirmed for the lower boundary of the interval of door sizes, the total execution time is growing strongly for smaller door sizes. But for a larger size of the door the total execution time seemes to relax faster than expected. With widths of the door of 2 rd a limit execution time seems to be achieved. This is shown in FIGURE 2. We again propose, that the behaviour of the robots near the door and the flow through the door is limited by the pure existence of "crowdedness" in front of the door - if there are any collisions in front of the door and any robots sticking, this strongly regulates the possibility of leaving the crowd. For the robots at the door the leaving time is limited by this effect, not of the time needed for just leaving the room itself through the door. For the lower boundary it is to mention, that the execution time gets enlarged by the robots sticking at the door frame.
Some of the effects could be caused by the setup of the controller whatsoever, since the goal of the robots is not localized in infinity, so that the robots drive straight forward, but the robots were focussing on a point quite near to the door itself.

Third the mean velocity limit of the robots was tested in steps like mentioned above. One would think, that the larger the velocity limit of the robot gets, the faster the entire group of robots would be able to escape. The measurements illustrated in FIGURE 3 on the other hand show that although the execution time decreases strongly hyperbolic for lower velocity limits, it hits a minimum execution time at roughly 12 velocity units (vu). This limit holds until the end of the series at a upper boundary of 20 vu. One can conclude that for velocities beyond 12 vu the increase of the velocity limit only leads to more collisions and an increase of the general crowdedness. This results align with the findings of the sited article [SDFEP]. (The relaxation of total execution time is found there also, the so called "the faster the slower"-effect could not be reproduced distinctly - maybe due to a naive collision model.)

Manipulating the velocity standard deviation of the Gaussian velocity distribution (note FIGURE 4) shows that with rising deviation the formerly constant robot flow through the door now starts to separate into groups. While the group of the fastest robots has almost no change in their execution time, the robot groups of lower velocity dominate the behaviour of the total execution time, which increases for large standard deviation values.

Comparing the velocity series for different door sizes (1.5 rd, 2.5 rd, 3.5 rd) as done in FIGURE 5, one can see, that in any case the total execution time relaxes hyperbolically on a certain lower limit. The absolute value of the total execution times lower limit differs with the size of the door, connecting lower time limits with the larger gate. (This correlation is only observed qualitatively, not quantitatively or analytically due to the large fluctuations for just little changes in the door size.)

Conclusion

From all series of measurement above we can conclude, that escape situations aren't solved by simply maximizing environmental and intrinsical parameters, but in contrast evacuation problems appear to be optimization problems in almost all parameters. This means, that a maximum of efficiency (which in this model would be measured by a minimal total execution time with least parameter effort) exists, that cannot be breached. It is nontrivially found by optimizing combined parameter series, for the relaxation of e.g. velocity and door size together do not lead to a relaxation on the same time value in combination. The parameters appear to not only manipulate the time parameter, but also the impact of other parameters on the time parameter, so that they are found to form a dependent parametric system.

Comparing our crowd of robots to an actual situation containing living and reacting beings we have to consider, that the last ones do not simply follow algorithms as the robots do, but adapt their behaviour to the immediate situation and choose deviating approaches. Some of them might even be less effective than the algorithmic ones. Based on the findings of [SDFEP] we assume that even for living beings our proposal that escape problems are optimization problems still applies to a large part.

Download

Download the manipulated code files here

Literature

1. [SDFEP] Helbing, Dirk, Illes Farkas, Tamas Vicsek: "Simulating dynamical features of escape panic.", Nature 407.6803 (2000): 487-490.
2. LPZ Robot Package & its documentation, Research Network for Self-Organization of Robot Behavior in Leipzig, Goettingen and Edinburgh