COMPLEX AND ADAPTIVE DYNAMICAL SYSTEMS - Prof. Dr. C. Gros

Student: Giulia Russo - Summer term 2020

Radial losses in a nuclear reactor core

Contents

• Introduction
• Operation
• Fundamentals of neutron transport theory: the diffusion model
• Monte Carlo simulations: design of a neutron reflector for a nuclear core
• Comments and conclusions
• References
• Further readings

Introduction

There are different types of Nuclear Power Plants (NPP) which differ by the energy spectrum of the neutrons that induce fissions. Below 0.3eV a NPP is a thermal reactor because neutrons are almost at thermal equilibrium with the surrounding matter; above 10keV a NPP is a fast reactor; in between we have the intermediate reactors. We'll focus on the first type of reactors because they're the most common and the very first that have been built and studied since the first fission reaction achieved by Fermi in 1942.

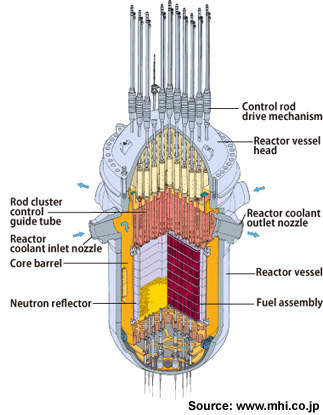
The nuclear reactor core is a very limited and confined space of a nuclear power plant where fission reactions occur. It has a cylindrical shape and the thermal cores are mainly composed by four elements:

• Nuclear fuel: containing a mixture of U-238 and U-235 (around 3% in weight)
• Water: responsible for cooling the core and thermalize the neutrons
• Boron: that absorbes neutrons
• Iron alloy: to keep fuel in place and define volumes where water can flow.

The fuel is organized in a very precise way: the smallest part is the fuel pellet, a cilinder of $\approx$1cm radius x $\approx$1.5cm hight. They are collected in rod of $\approx$4m height (fuel rods) then collected in the fuel assembly of 14 (or 17) x 14 (or 17) rods. To have some numbers in mind: a NPP for electricity production has approximatelly around 176 (or 264) fuel rods per assembly and between 121 and 193 assemblies in the core. It is easy to notice that $14^2 > 176$, part of the remaining places are occupied by instrumentations but the majority is occupied by the so called control rods. As the name says, these particular rods are installed at the place of fuel rods. They are made by materials able to absorb neutrons therefore a change in the power produced by the reactor can be easily achieved by changing the axial position of some of them. Moreover, the insertion of all the rods causes the complete shut-down of fission reactions, this process is called scram.

Operation

The fuel is an oxide mixture of U-238 and U-235. The latter is called fissile material thanks to its ability to undergo to fission when hit by a low energy neutron, the first is called fertile due to its ability to transform into a fissile by neutron capture; therefore, it's able to produce the fissile needed to keep the reaction going. In nature there are different types of fissiles U-233, Pu-239, Pu-241, but U-235 is the only one that occurs in a usable ammount (almost 0.72% in weight).

The ammount of U-235 is defined as the enrichment and for safety reasons it cannot exceed the 3%-4% in weight. Of course, other type of reactors can have different percentages: the High Temperature Gas Cooled (HTGC) reactors can reach the 7%-20% or the Fast Liquid Metal Reactors (LMR) between the 15%-20% (of Pu). Due to the high content of fissile materials in the core, this reactors have to handled cautiously. (But this topic is a way more wide than what I could explain here, since all the industrial process that lead to enrich the fuel should be taken into account).

It is important to understand that U-235 is an unstable element, so it will spontaneously undergo to a nuclear transmutation that will bring it to a more stable state. This transmutation is nuclear fission and will lead to an emission of $\nu$ neutrons in a certain energy range. The minimum amount of fissile material needed for a sustained nuclear chain reaction is called critical mass. The nuclear chain reaction occurs when the average amount of neutrons produced by nuclear fission is larger than those absorbed and lost. Therefore, all NPP contain an amount of fissile material larger than the critical mass, so that when the core is switched on for the very first time there is no need for an external source of neutrons. Then, between 1.5y up to 3y of operation, the opertators will move the control rods in the core, change the content of Borum diluited in water in order to produce the eletrical power required by the grid and try to consume the fuel in the most homogeneous way. In reality, this last point is not really achieveble, thus every 2y (on average) refueling operation occurs: fuel assemblies are moved in other part of the reactor, some are removed and new one are inserted. How and where to move fuel assemblies in the reactor, as well as how much U-235 insert in the new fuel assemblies is known as criticality calculation because, as we said, we aim to have a bit more than the critical mass at each restart. When the core contains exactly the critical mass, it is called critical (k=1), if it's slightly below this value is said sub-critical (k<1) and supercritical (k>1) otherwise.

The majority of the neutrons will be emitted immediatelly after the event ($10^{-17}$s) others with some delay. The first are called prompt neutrons, the latter delayed neutrons. As all the nuclear reactions, there is a certain probability that a certain reaction occurs and in general after a fission event there could be from 0 up to 5 neutrons emitted. There are two important parameters that influece the outcome of this event:

• The energy of the incident neutron
• The number of neutrons emitted by a certain isotope: $\nu_0$

$$ \begin{aligned} \nu(E) = \nu_0 + constant * E \end{aligned} $$

Element	$\nu_0$	Energy [MeV]
U-235	2.35	>1MeV
U-235	2.43	0-1 Mev
U-238	2.30	All energies

It is intuitive to understand that as soon as the fission reaction starts, it self-suistains and, in absence of any control, the number of neutrons emitted will rapidly increase. On the one hand, it is important to build a reactor that is able to self-sustain the reaction chain (otherwise we'll need an external source of neutrons to keep alive the reaction), on the other hand it is even more important to be able to properly control (and in some cases "switch off") this chain. The long term control of the reaction (like, for example, the change of the power produced) is performed by changing the vertical position of control rods; while the short term control is performed by the Boron diluted in the cooling water.

Talking about the criticality of a core, we introduced the parameter k, it is called effective multiplication factor and is given by:

$$ \begin{aligned} k_{eff} = \frac{\text{neutrons produced by fission in one neutron generation}}{\text{neutron lost by absorption and leakages in the preceding neutron generation}} \end{aligned} $$

The term neutron generation is used to refer to the "life" of a group of neutrons from birth to the time they're absorbed to induce fission and therefore, produce new neutrons that will be part of the next neutron generation.

The core has an effective multiplication factor slightly larger than one, this allows to have a self-sustained reaction. As we see the two main sources of losses of neutrons are parasitic absorptions (by surrounding metal structure, cooling water, fission products, ...) and leakages (neutrons escape from the boundary of the core). To understand which parts are more affected by these losses we're supposed to have a good understanding of how the neutrons distribute in the reactor, therefore the shape of the flux as a function of space (thanks to the cylindrical symmetry just the axial and radial position are considered) and time.

Fundamentals of neutron transport theory: the diffusion model

The distribution of neutrons inside the core is given by the Boltzmann's Transport Equation. It's derivation won't be reported but it's important to understand the meaning of the different terms in order to introduce later on a simpler model and study it's solution. The demonstration could be found in Neutron Transport Theory by Davison and Sykes.

$$ \begin{aligned} \frac{d}{dt}\int_{V} N(\mathbf{r},v,t) dV = \text{production rate} -\text{absorption rate} - \text{leakage rate} \end{aligned} $$

$$ \begin{aligned} \frac{d}{dt}\int_{V} N(\mathbf{r},v,t) dV = \int_{V} S(\mathbf{r},t) dV - \int_{V}N(\mathbf{r},v,t) v \Sigma_c (\mathbf{r},v,t) dV - \oint J(\mathbf{r},v,t) \cdot \mathbf{n} dA \end{aligned} $$

Reading the previous equation from left to right we find out that:

The local rate of change in the average neutron density ($N$) is due to the local rate of neutrons added by the source ($S$, i.e. neutron fissions) minus those captured ($N \cdot \Sigma_c$) and those flowing out the local surface ($J \cdot dA$).

The diffusion model is the simplest model to understand the shape of the neutron flux $\phi$ in a core as a function of time and space. The events related to a NPP occur on two completely different time scales: on the time scale of the fission events the neutron flux is almost constant, while on the time scale of a human observer the flux changes in time. In particular, leakages and capture phenomena occur on time scales longer than the fission events. In the first case, neutrons have to travel all the radial distance of the core (except if they're produced nearby the boundaries) while in the latter one, they have to be slow down enough to be actually "seen" by the atoms (right now it's not important if the absorption will produce or not a fission, in the latter case the capture is said parasitic). From a mathematical point of view it means that we're asking the fractional change in the neutron flux to be small during the time required by a neutron to travel three mean free paths. In particular, the following evaluation is made in the most conservative way (i.e. for the slowest neutrons in the reactors that travel at an average speed of $1000$m/s = $10^5$cm/s):

$$ \begin{aligned} \Big|\frac{1}{\phi} \frac{d \phi}{dt}\Big| << \frac{10^5}{3\lambda_s} \frac{1}{s} \end{aligned} $$

Assumptions:

• The medium is uniform (we'll define average cross sections for the different phenomena);
• There are no external neutron sources, the only source of neutrons are fissions;
• Isotropic scattering in the laboratory reference system;
• The neutron flux is a slowly varying function of the position;
• We neglect the effect of possible present reflector.

The Diffusion Equation

$$ \begin{aligned} D \nabla ^2 \Phi (r,z) - \Sigma _a \Phi(r,z) + S(r,z,t) = \frac{1}{v}\frac{\partial \phi(r,z)}{\partial t} \end{aligned} $$

The critical passage to move from the integral form of the neutron transport equation to the partial differential equation above underlies on the set of assumptions made before and the use of Fick's law that allows to relate the neutron current with the neutron flux. Of course, this has some implications on the result we'll obtain but they'll be discussed later on.

It is possible to further simplify the calculations by using the fact that the core has a cylindrical symmetry. Therefore, the steady state solution of the diffusion equation is determined and it reads as follows:

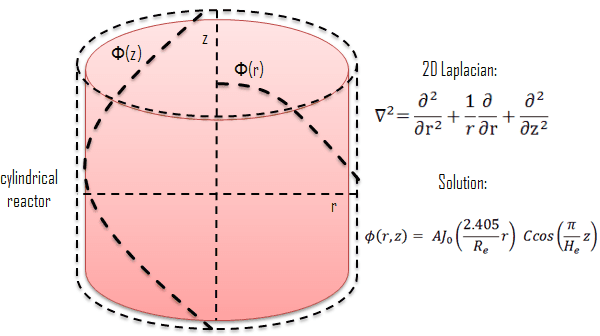
Where,

$A$ and $C$ are integration constants. We see that the axial flux is modulated with a cosine, while the radial component is modulated by a Bessel function. The quantities $R_e$ and $H_e$ are the extrapolated radius and extrapolated height, respectivelly.

The diffusion model is not valid near the boundaries due to the fact that we used many assumptions. Nevertheless, physical boundary conditions will be imposed and it will be possible to prove that the mathematical model won't be violqted. We ask the neutron flux to be zero at a radius (the same can be said for the axial direction) slightly larger than the core one: this distance is called extrapolated radius. From a physical point of view, this is not true, but it's a very powerful mathematical artifact in order to have simple analytical solutions. The detailed and precise description of the neutron flux nearby the boundaries is give just by the exact transport theory.

Monte Carlo simulation: design of neutron reflector for a nuclear core

We now know how the neutrons distribute inside a core, but still we have to understand what happens to a neutron after it is generated by a fission event.

As reported in the table in the Operation section, the energy spectrum of the neutrons emitted by a fission is pretty wide, but only thermal neutrons (0.025eV) are able to induce fissions. Fast neutrons are able to induce fissions as well but due to the small cross section their contribution can be neglected, as a first approximation. It is then obvious that they have to be strongly slow down before they're able to be captured by U-nuclei. This work is performed by water, thanks to the collision with these molecules, neutrons progressively lose their energy. At these energies and far from the boundaries, scattering can be considered almost isotropic. But as it was said at the beginning there is a certain amount of Boron in water which aims to capture neutrons. Therefore, when we give an estimation of the average scattering cross section we should considered that Boron and other pollutants (such as fission products) are diluited in water and that the scattering cross section of each of them changes as a function of the energy of the incident neutron and of the temperature of the system.

A similar rationale can be adopted to estimate the fission cross section. As we said, the fuel is not uniformely burned inside the core, therefore we expect to have an axial dependence (we could neglect the radial one since the rods have a small radius) but (also in this case) more important is the energy dependence (we assum to neglect any transient so that the temperature of the fuel can be considered almost constant).

Last but not least also parasitic absorptions must be considered. Under this name we collect all the absorptions performed by control rods, Boron, pollutants and fuel (that don't lead to fission). It's now intuitive to understand that we have a dependence on energy and temperature, but in this last case it is more important to consider that different material have completely different cross sections.

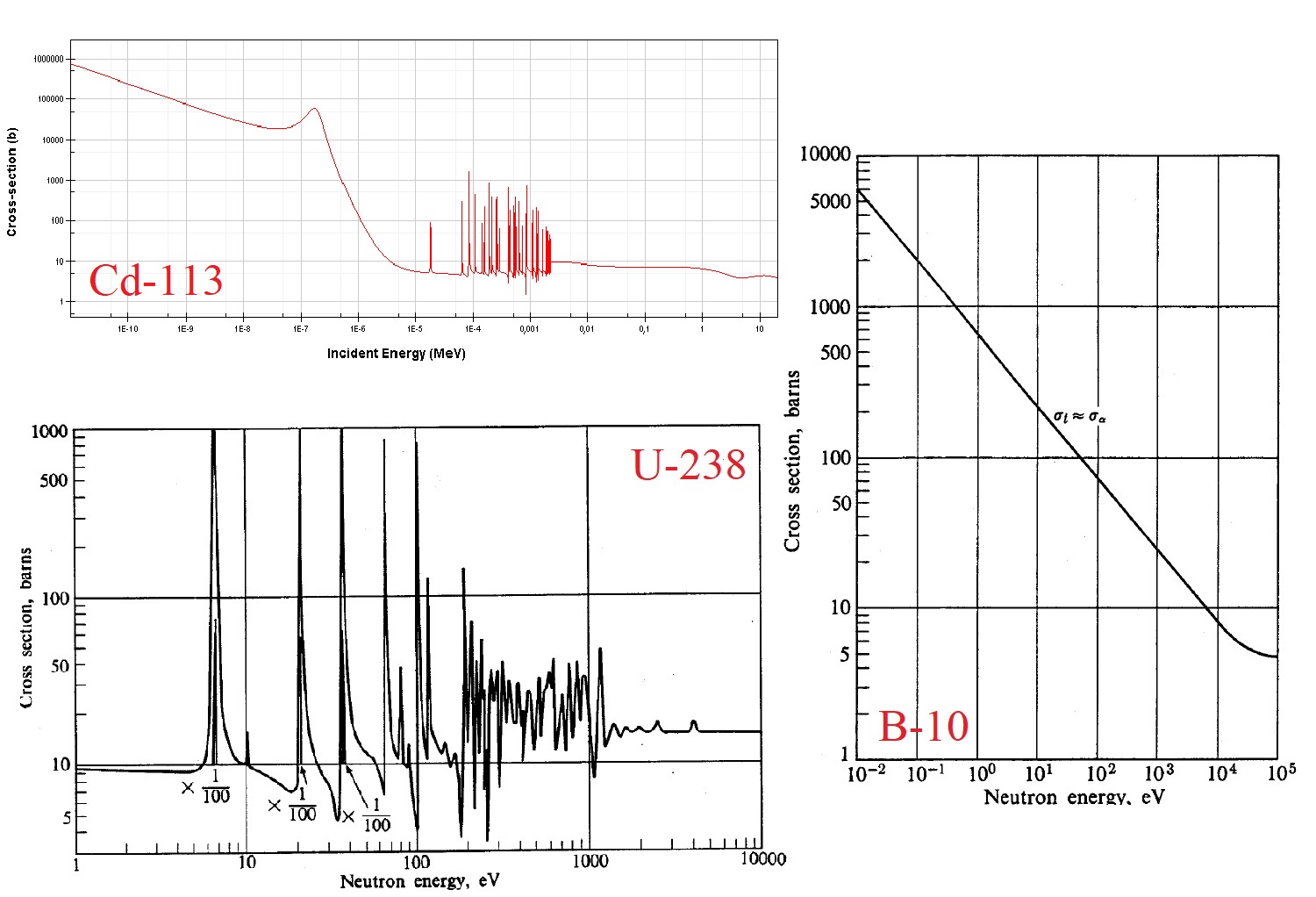
The values adopted in the simulation are purely qualitative. Since we want to understand how effective a neutron reflector is by varying its thickness and its scattering "capabilities" (i.e. the scattering cross section), we have to fix some parameters:

• Radius of the core will be constant and equal to 6.5 m;
• In the reflector we just have absorptions and scattering and of course the scattering probability has to be larger than the absorption one. Since we just have this two phenomena, we fix one of the two parameter and the other is determined as the complementary to 1.0;
• In the core we have fissions and scattering (we neclect the parassitic absorptions) and in this case the fission probability has to be larger than the one for scattering;
• We assume that the scattering cross sections in the core and in the shield are constant. The first one will be fixed while the latter will be changed.

Monte Carlo codes rely on repeated random sampling to obtain numerical results, therefore we have to define a tolerance and once the error will reach that value we will stop the analysis and move to the other case study. What we want to estimate is the effectiveness of the neutron reflector.

Before moving to the study of the results a very last comment. The axial motion of the neutron is not considered because usually the reference system is located at half the height of the core and we're performing a study on the radial losses through the boundaries.

import numpy as np
import matplotlib.pyplot as plt
import random as rn
import time
from prettytable import PrettyTable

pA = 0.05
pF = 0.85
R0 = 6.5 # Radius of the core is fixed
sigmaS_core = 0.3
toll = 2./100
ps = 1 - pA
col = ["blue", "orange", "red", "green"]

start_time = time.time()
for R in np.linspace(7.0,8.6,4):   
    table = PrettyTable(['Scattering cross section of the reflector','Leakages','Additional fissions','Parassitic absorptions'])
    sigma_vector = np.linspace(0.3, 0.9, 4) #scattering cross sections of the reflector
    col_labels = ['scattering','absorption','fissions']
    row_labels = ["%1.3f" %ss for ss in sigma_vector]
    f0, (ax1,ax0) = plt.subplots(nrows=1, ncols=2, sharex=False, sharey=False, figsize=(12,6))
    f0.suptitle(str("Neutron reflector thickness: %1.3f m" %(R-R0)), size = 15)
    #Transverse section core
    ax1.plot(R*np.cos(np.linspace(0,2*np.pi,100)),R*np.sin(np.linspace(0,2*np.pi,100)), label = "Neutron reflector")
    ax1.fill(np.append(R0*np.cos(np.linspace(0,2*np.pi,100)),R*np.cos(np.linspace(0,2*np.pi,100))[::-1]), np.append(R0*np.sin(np.linspace(0,2*np.pi,100)),R*np.sin(np.linspace(0,2*np.pi,100))[::-1]),alpha=0.4)
    ax1.plot(R0*np.cos(np.linspace(0,2*np.pi,100)),R0*np.sin(np.linspace(0,2*np.pi,100)), label = "Reactor core")
    ax1.fill(np.append(R0*np.cos(np.linspace(0,2*np.pi,100)),0), np.append(R0*np.sin(np.linspace(0,2*np.pi,100)),0),alpha=0.4)
    ax1.legend()
    ax1.axis('equal')
    ax1.set_xlabel ("x", size = 13)
    ax1.set_ylabel ("y", size = 13)
    ax1.grid()
    for h,sigmaS in enumerate(sigma_vector, start = 0):
        err = 1.0
        i = 0
        csi = [] #statistical variable
        SampleAverage = [] #mean
        mom_2 = [] 
        variance = []
        PRSD = [] #Percentage relative s.t.
        absorptionReflector = 0
        newFission = 0
        escaped = 0
        while(err>toll or i<100):
            i += 1
            #Isotropic source at r=R0 for a fix emission angle (we use polar symmetry)
            x0 = R0 * np.cos(np.pi/4.0)
            y0 = R0 * np.sin(np.pi/4.0)
            life = 1 #Neutron just escaped
            #Random generation
            mu = -1 + 2*rn.random()
            phi = 2*np.pi*rn.random()
            csi_temp = 0
            sigma = sigmaS
            while life == 1:
                free_path = -1/sigma * np.log(rn.random())
                x = x0 + np.sqrt(1-mu**2)*np.cos(phi)*free_path
                y = y0 + np.sqrt(1-mu**2)*np.sin(phi)*free_path
                if np.sqrt(x**2+y**2)>=R:
                    life = 0
                    csi_temp = 1 #we have a leakage!
                    ax1.plot(x,y,"x", color = col[h])
                    escaped += 1
                elif (np.sqrt(x**2+y**2)<R and np.sqrt(x**2+y**2)>=R0):
                    if rn.random()<pA:# we have an absorption in the reflector
                        life = 0
                        absorptionReflector += 1
                    else: #We have scattering --> new random generation
                        x0 = x
                        y0 = y
                        mu = -1 + 2*rn.random()
                        phi = 2*np.pi*rn.random()
                        sigma = sigmaS
                else: #after reflection the neutron go back into the core
                    if rn.random()<pF:# we have an absorption with fission
                        life = 0
                        newFission += 1
                        ax1.plot(x,y,".", color = col[h])
                    else: #We have scattering --> new random generation
                        x0 = x
                        y0 = y
                        mu = -1 + 2*rn.random()
                        phi = 2*np.pi*rn.random()
                        sigma = sigmaS_core
            csi.append(csi_temp)
            SampleAverage.append(sum(csi)/i)
            mom_2.append(sum(np.array(csi)**2)/i)
            variance.append(np.array(np.array(mom_2)-np.array(SampleAverage)**2))
            PRSD.append(np.array(np.sqrt(np.array(variance[-1])/i)/np.abs(np.array(SampleAverage)))) 
            if np.array(PRSD[-1][-1])>0:
                err = np.array(PRSD[-1][-1])
        # Sample average
        ax0.plot(SampleAverage, label = "$\u03A3 _s$ = %1.3f" %sigmaS)
        ax0.set_title("Sample average", size = 13)
        ax0.set_xlabel("iterations", size = 13)
        ax0.legend()
        
        norm_factor = absorptionReflector + newFission + escaped
    
        r1 = ["%1.3f" %sigmaS, "%1.2f %%" %(SampleAverage[-1]*100), "%1.2f %%" %(absorptionReflector/norm_factor*100), "%1.2f %%" %(newFission/norm_factor*100)]
        table.add_row(r1)
        
    ax0.grid()
    plt.show()
    print(table)
    
print("\n\n")    
print("Time needed for the simulation: %1.2f seconds" % (time.time() - start_time))

/usr/local/bin/start_ipykernel.py:75: RuntimeWarning: invalid value encountered in true_divide
/usr/local/bin/start_ipykernel.py:76: RuntimeWarning: invalid value encountered in greater

+-------------------------------------------+----------+---------------------+------------------------+
| Scattering cross section of the reflector | Leakages | Additional fissions | Parassitic absorptions |
+-------------------------------------------+----------+---------------------+------------------------+
|                   0.300                   | 50.45 %  |        1.71 %       |        47.84 %         |
|                   0.500                   | 43.77 %  |        1.96 %       |        54.27 %         |
|                   0.700                   | 39.71 %  |        2.08 %       |        58.21 %         |
|                   0.900                   | 38.60 %  |        2.51 %       |        58.88 %         |
+-------------------------------------------+----------+---------------------+------------------------+

+-------------------------------------------+----------+---------------------+------------------------+
| Scattering cross section of the reflector | Leakages | Additional fissions | Parassitic absorptions |
+-------------------------------------------+----------+---------------------+------------------------+
|                   0.300                   | 46.58 %  |        2.75 %       |        50.66 %         |
|                   0.500                   | 37.48 %  |        2.95 %       |        59.57 %         |
|                   0.700                   | 34.15 %  |        4.37 %       |        61.48 %         |
|                   0.900                   | 30.92 %  |        5.17 %       |        63.91 %         |
+-------------------------------------------+----------+---------------------+------------------------+

+-------------------------------------------+----------+---------------------+------------------------+
| Scattering cross section of the reflector | Leakages | Additional fissions | Parassitic absorptions |
+-------------------------------------------+----------+---------------------+------------------------+
|                   0.300                   | 42.17 %  |        3.29 %       |        54.53 %         |
|                   0.500                   | 32.75 %  |        4.95 %       |        62.31 %         |
|                   0.700                   | 27.66 %  |        5.87 %       |        66.47 %         |
|                   0.900                   | 24.28 %  |        7.36 %       |        68.37 %         |
+-------------------------------------------+----------+---------------------+------------------------+

+-------------------------------------------+----------+---------------------+------------------------+
| Scattering cross section of the reflector | Leakages | Additional fissions | Parassitic absorptions |
+-------------------------------------------+----------+---------------------+------------------------+
|                   0.300                   | 39.32 %  |        3.73 %       |        56.95 %         |
|                   0.500                   | 29.79 %  |        6.04 %       |        64.17 %         |
|                   0.700                   | 24.77 %  |        7.25 %       |        67.98 %         |
|                   0.900                   | 20.46 %  |        8.61 %       |        70.93 %         |
+-------------------------------------------+----------+---------------------+------------------------+



Time needed for the simulation: 1234.27 seconds

Comments and conclusions

The general comment is that the more we increase the thickness of the reflector the longer it takes to run the simulation due to the fact that we're implicitly increasing the number of collisions that neutrons will perform in the reactor and therefore their "life". At constant thickness, a change in the scattering cross section induces strong modifications in the results.

Let's consider the case where the thickness is equal to 1.567m. Increasing the cross section we observe an increase in the scattering events in the reflector, i.e. a reduction in the leakages. Moreover, we observe an increase of the number of fissions (neutrons are scattered back into the core where they induce fissions) as well as parasitic absorptions in the reflector. This phenomenon can be intuitively explained considering that at high scattering cross sections the neutrons will undergo to a higher number of collisions, therefore, the probability to be back-scattered in the core as well as the probability of being absorbed in the reflector is increased. The most important feature is a strong reduction (almost halved) in the leakage probability. Of course, it is important to find a trade-off between the phenomena. The most important are the reduction of losses and parasitic absorptions, while the least important is the contribution of additional fissions. This is the reason why several simulations have been performed varying the radial dimension of the reflector. Increasing the thickness of the reflector we observe a reduction of the leakages when the scattering cross section of the material is increased. Moreover, this value is almost halved, except for the first case where the reflector is definetely not thick enough. At the same time, it is possible to observe that the parasitic absorptions get more and more important when the thickness is increased.

The main reason to install a neutron reflector is the increase of the neutron flux at the boundaries, which means having a flatter radial flux and therefore a more uniform consumption of the fuel. The reduction of losses induces a lower activity of the surrounding materials (mainly the pressure vessel).

Commonly, neutron reflectors are made by graphite, beryllium, steel or tungsten carbide (but these are just examples) and their lenght can vary between 5cm up to 3m according to the type of reactor we're considering. The choice of the material, therefore, strongly depends on the energy of the incident neutron; in fact, some materials may show a very high scattering cross section but in the wrong energy range.

References

• J. R. Lamarsh - Introduction to nuclear reactor theory - Addison-Wesley
• Personal notes of the course Nuclear reactor physics by Prof. Dr. Piero Ravetto at Politecnico di Torino - academic year 2016/2017.

Further readings

• J. B. Davison and B. Sykes - Neutron transport theory - 1958
• G. I. Bell and S. Glasston - Nuclear reactor theory - 1970 (if you wanna know learn how to solve the neutron transport equation)