Counterflows: |
 |
 |
 |
optimal counterflows |
with "frictions" |
"freezing by heating" |
by Frederik Depta, Lijuan Liu and Nibras A Suleman
Nowadays, with an increasing number of urban population and also a huge number of social events, the analysing the collective human behaviour is getting more important. Especially when it comes to the behaviour of crowd in panic situations. This project of ours, based on the works of the Institute for Economics and Traffic in Dresden, Institute for Advanced Study and Department Biological Physics both from Budapest, investigates the behaviour of the crossing of two pedestrian stream, which simulates a jamming of pedestrians e.g in a panic situation. This applet simulates two pedestrian streams intersecting with an adjustable angle.
Counterflows: |
 |
 |
 |
optimal counterflows |
with "frictions" |
"freezing by heating" |
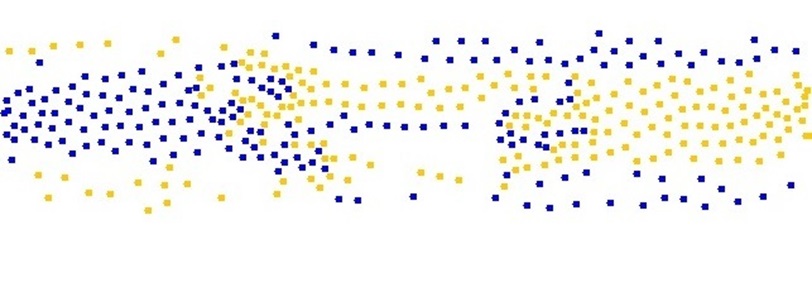
In counterflows, the two pedestrian streams intersect with an angle of 180°. The pedestrian streams will be divided into several lanes in walking direction. This segregation phenomenon reduces the number of encounters with oppositely moving pedestrians, i.e. the interaction frequency and number of necessary breaking or avoidance maneuvers. As a result, the efficiency of walking is maximized. Therefore, this phenomenon can be viewed as a prime example of optimal self-organization.
The number of lanes depends on the width and length of the walkway, fluctuations and disturbances. The shape of the lanes is time dependent, as in other two-fluid flows. If pedestrian crowds moving in opposite directions meet each other, they form small channels at first, and then these channels merge to produce wider lanes. This phenomenon is related to fluctuation-induced ordering and reduces the number of events with high "friction" due to opposite directions of motion.
In cases of extreme densities, large disturbances, or nervous pedestrian crowds, ordered lanes can break down due to relentless overtaking maneuvers. Then, blocks of pedestrians with opposite desired directions of motion face each other, but cannot progress. This phenomenon is called "freezing by heating" and may emerge in counterflows of panicking pedestrians.
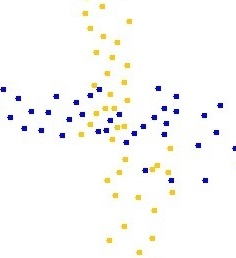
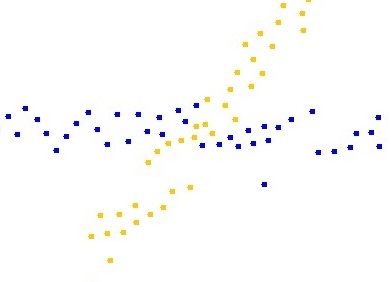
Intersecting flows: |
 |
 |
 |
|
\begin{array}{r l} \vec{f}_{\alpha} (t) = \vec{f}^{0}_{\alpha}(\vec{v}_{\alpha})+ \vec{f}_{\alpha B} (\vec{r}_{\alpha})+ \sum_{\beta \neq \alpha} \vec{f}_{\alpha \beta} ( \vec{r}_{\alpha}, \vec{v}_{\alpha}, \vec{r}_{\beta}, \vec{v}_{\beta}) + \sum_{i} \vec{f}_{\alpha i} (\vec{r}_{\alpha}, \vec{r}_{i}, t) \end{array}
The force of $ \vec{f}_{\alpha B} (\vec{r}_{\alpha}) $ is the repulsive effect from the pedestrian $\alpha$ to the boundaries. Thus, it can be set to zero for our simulation.
The sum of forces in $ \sum_{i} \vec{f}_{\alpha i} (\vec{r}_{\alpha}, ...) $ is the long range interaction between the pedestrians as seen in a group of pedestrians and families. It can also represent the attraction of an display on the boardwalk or a street artist. For our simulation it is set to zero.
The force $ \vec{f}^{0}_{\alpha}(\vec{v}_{\alpha})= \frac{1}{\tau}(\vec{v}^{0}_{\alpha}-\vec{v}_{\alpha}) $ is the acceleration force on the pedestrian $\alpha$ due to the desire to walk in a certain direction with $\vec{v}^{0}_{\alpha} = v^0_\alpha (t) \cdot \vec{e}^0_\alpha$ being the desired and $\vec{v}_{\alpha}$ being the actual velocity of the pedestrian. $\tau$ is the relaxation time due to disturbances in the movement caused by the manoeuvres of the pedestrians and it is set to $\tau=1s$. $v_\alpha^0 (t)$ is modelled by the following function: \begin{array}{r l} v^0_\alpha (t) = & [1-n_\alpha (t)]v^0_\alpha (0) + n_\alpha (t) v_\alpha^{max} \\ n_\alpha (t) = & 1 - \frac{\overline{v}_\alpha (t)}{v^0_\alpha (0)} \end{array}
Where $v^0_\alpha (0)$ is the desired velocity at $t=0$, $v_\alpha^{max}$ is the maximal desired velocity and $\overline{v}_\alpha (t)$ is the average velocity of the pedestrian in the desired walking direction $\vec{e}^0_\alpha$.
The repulsive force from pedestrians $\alpha$ to $\beta$ is given by the sum over \begin{array}{r l} \vec{f}_{\alpha \beta}(t) = & A^{(1)}_{\alpha}exp \lgroup (r_{\alpha \beta}-d_{\alpha \beta})B^{-1}_{\alpha} \rgroup \vec{n}_{\alpha \beta} \\ & \cdot \lgroup \lambda_{\alpha} + 0.5 \cdot (1-\lambda_{\alpha})(cos(\varphi_{\alpha \beta})+1) \rgroup \\ & +A^{(2)}_{\alpha}exp \lgroup (r_{\alpha \beta}-d_{\alpha \beta})B^{-1}_{\alpha} \rgroup \vec{n}_{\alpha \beta}, \; \end{array}
$ $
with $ r_{\alpha \beta}=(r_{\alpha}+r_{\beta})$ the sum of radii of the pedestrian,
${d}_{\alpha \beta} (t) =||(\vec{x}_{\alpha}(t)+\vec{x}_{\beta}(t))|| $ the distance (between the centers of mass) of pedestrains $\alpha$ and $\beta$,
and $\vec{n}_{\alpha \beta}=[\vec{x}_{\alpha}(t)+\vec{x}_{\beta}(t)] \cdot d^{-1}_{\alpha \beta}(t) $ the normalized vector pointing from pedestrian $\beta$ to $\alpha$.
For the anisotropic character of the interactions $\lambda_{alpha}$ is set to $0.75$, so for every pedestrian only the front matters and the happening in the behind is not considered for the motion.
$A^{(1)}_{\alpha}$ (in the first term of the equation) is the private zone of every pedestrian. This coefficient helps to avoid collisions. Obviously in crowded situations like this the personal comfort zone doesn't matter as seen in the following schematic representation. And to speed up the simulation, it is set to zero.

The second term in the force $\vec{f}_{\alpha \beta}(t)$ represents the interactions in crowded situations. $B^{-1}_{\alpha}$ is the range of the repulsive interaction. $A^{(2)}_{\alpha}=3\frac{m}{s^{2}}$ denotes the respective interaction strengh and $B$ is adjustable.