Pattern Formation in the Gray-Scott Reaction-Diffusion System
Description of the System
The presented system describes the dynamics of two interacting variables U(x,t) and V(x,t) defining a density distribution of two chemical substances in two dimensions. The modeled chemical system can be scetched in the following way:
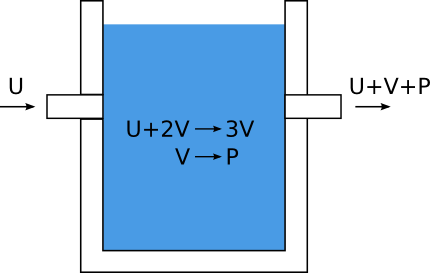
The evolution of both variables over time are defined through two first-order differential equations:
Here, the -terms correspond to the reaction
,
to the reaction
and
and
to the inflow and outflow respectively. The dynamic of the inert substance P does not influence the dynamics of U and V and therefore does not have to be considered. The terms
and
describe the diffusion of the substances in the volume (or, to be precise, in the area, since the system is modeled in two dimensions in this case).
The Applet
Controls/Explanation
- Two things are plotted by the applet during the simulation: One plot which shows the density-distribution of U by a color-coding. Black stands for U=1, green stands for U=0.2 (roughly) and blue blends between both colors/values. The other plot is a plot of all points of the 2d-grid used in the simulation and their current position in the U-V phase-space. Additionally, the green line represents the isocline of U and the red line represents the isocline of V for the dynamical system without the diffusive terms.
- The "set"-button sets all the manipulable internal parameters to the values that where entered into the text fields.
- The list with elements called "Solitons", "Worms", "Mazes" etc. carries a set of parameters which will guide the user to typical types of patterns which can be observed in the system.
- With the scrollbar one can add an additional delay to each timestep which will cause the simulation to be played slower.
- "switch plots" and "clear" should be self-explanatory.
- "U(paint)" and "V(paint)" specifies the values for U and V which are imposed onto a small circular area of the density distribution around the mouse-pointer, when the big square area is clicked somewhere. It still works if the big area displays the phase-space plot instead of the density distribution. However, you will see the effects of your painting in the scaled down version on the upper right.
- The red dots in the phase-space plot shows the current state of the coordinate the mouse is pointing at.
Theory
To understand the dynamics of the system, one can first look at the dynamics without the diffusive terms:
The fixed points of the system can be found to be
The Jacobian of has eigenvalues -F and -K and is therefore always stable.
The two other two fixed points only exist, if the term in the square root is positive:
Looking at , one finds, that given the existence of this fixed point, it is always a saddle:
on the other hand, is never a saddle, and by looking at the trace of
, one finds that this fixed points changes from stable to unstable if
.
Furthermore, one can also observe a transition between a stable node and a rotating focus, but this transition is of no importance for the occurence of patterns.
One can map the parameter values at which the types of patterns listed in the applet occur onto the phase-space together with the separatrices just described:
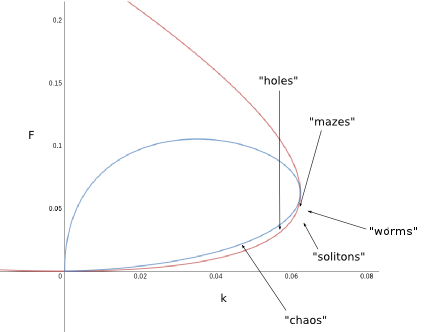
It turns out that patterns form mostly in the regime of only the trivial (1,0)-fixpoint but close to the separatrix defining a saddle-node bifurcation. The chaotic behaviour can be found in the regime enclosed by both lines.
Turing instability is often considered to be responsible for pattern formation, but cannot be applied to this case, since one cannot find a Diffusive term which would make the Jacobian
of the trivial fixed point unstable if it where added.
References
- John E. Pearson: "Complex Patterns in a Simple System", SCIENCE VOL.261
- Claudius Cros: Script on Self-Organization, SoSe 2014