Characteristic Gradients of Density
Characteristic Gradients of Density
The gradient expansion (GE) of the
exchange-correlation (xc) energy of density functional theory
includes the inhomogeneity corrections to the xc-energy of the
homogeneous electron gas in a systematic fashion.
Its basic ingredients are the gradients of the ground state
(spin-)density n(r).
The lowest order contribution to the GE, depending on
[grad(n)]2, is rigorously
determined by the long wavelength limit of the linear response
function of the homogeneous electron gas.
The first principles evaluation of higher order gradient terms
requires knowledge of higher order contributions to the long
wavelength expansion of the linear response functions and of
nonlinear response.
The convergence of the GE (or the GE-based functionals) and thus
its applicability depend on the actual size of the gradients.
In practice, of course, only the lowest gradients are of interest.
The appropriate dimensionless form of these gradients is obtained
by analysis of the long-wavelength expansions of the response
functions.
For the first gradient one finds
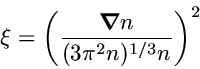
while the second gradient enters the GE in the form
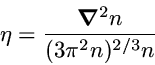
In terms of these quantities the exchange functional has a
particularly simple form,
![E_x[n]](xieta/img3.png)
The convergence of the GE thus requires that the product of the
characteristic gradients with the corresponding prefactors is
smaller than 1.
As the prefactors turn out to be smaller than about 0.1 the
gradients should be of the order of (or smaller than) 1.
Below these quantities are shown for a number of systems, ranging
from atoms to solids.
The densities used for these plots have been obtained by selfconsistent
calculations with the exact exchange.
However, the characteristic gradients are rather insensitive to the
particular density utilized.
The units of the plots are as follows:
All length scales are given in Bohr.
The characteristic gradients themselves are dimensionless.
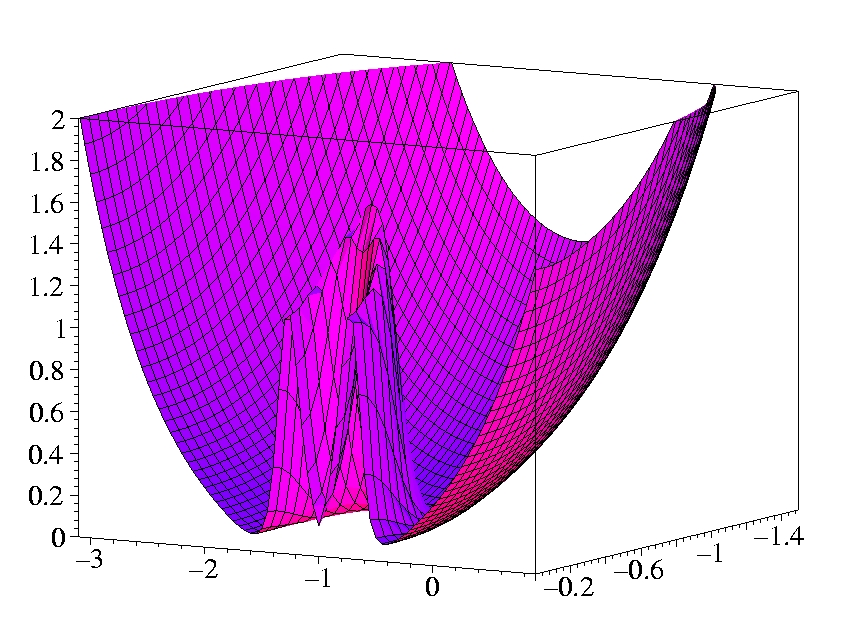
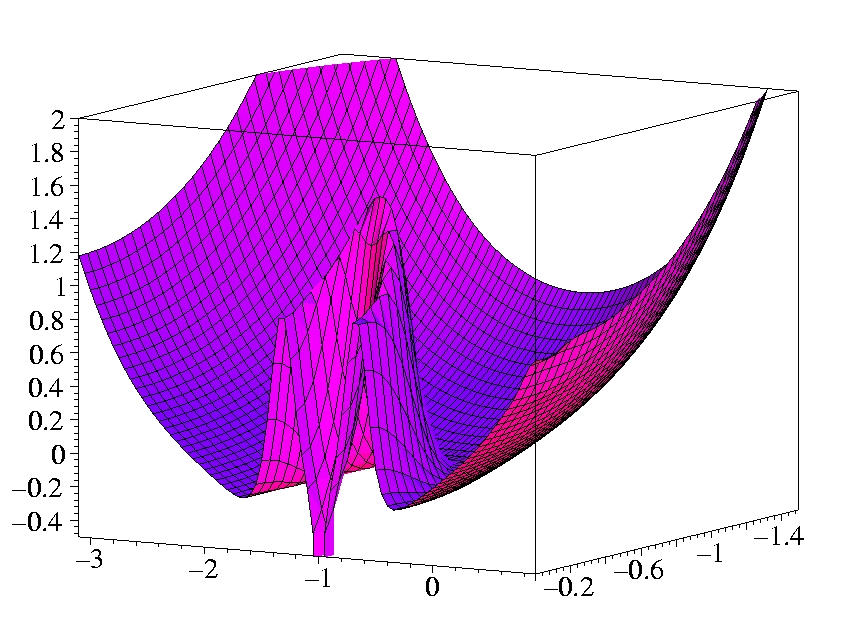
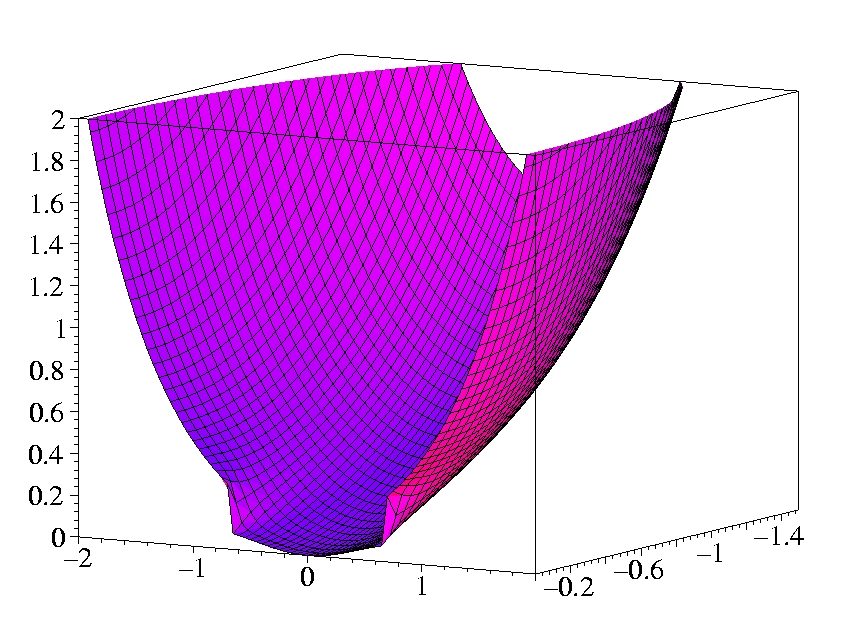
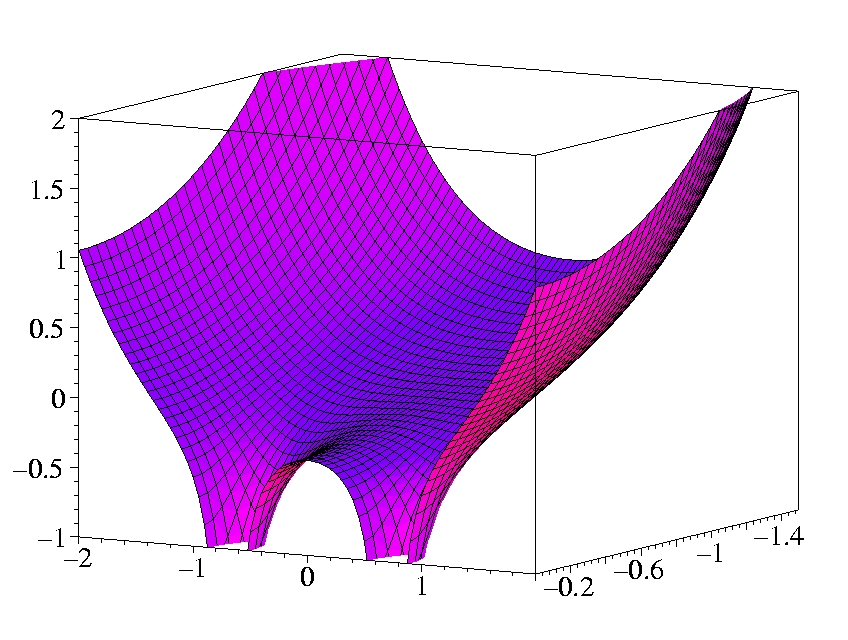
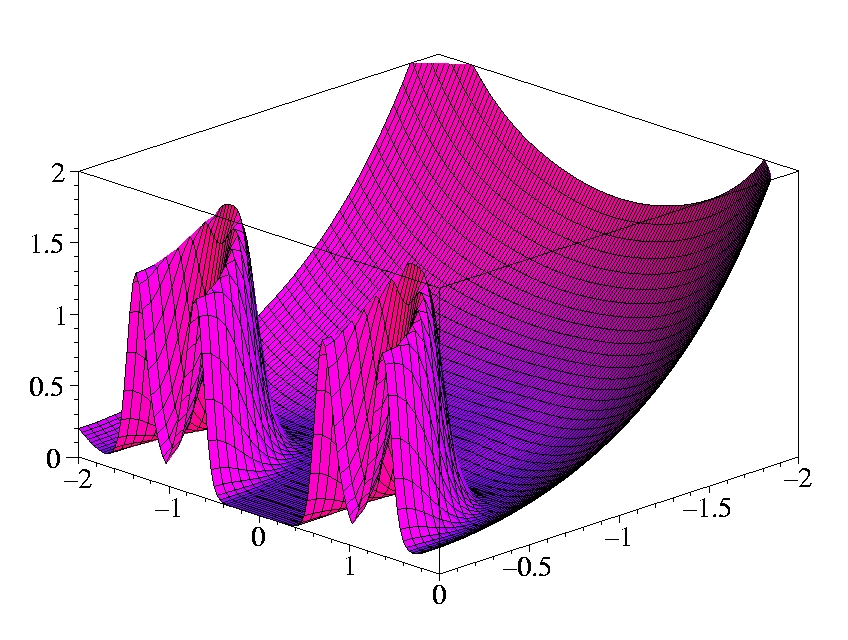
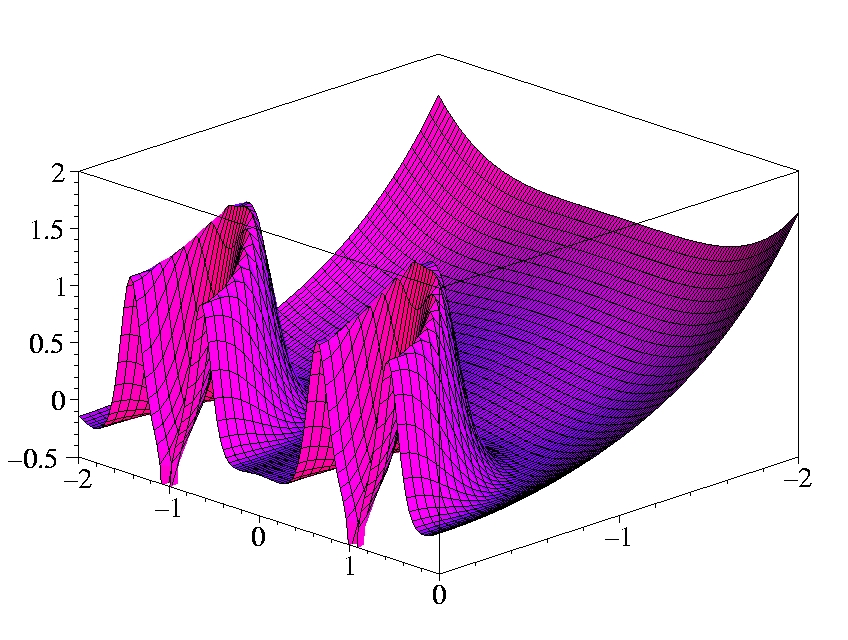
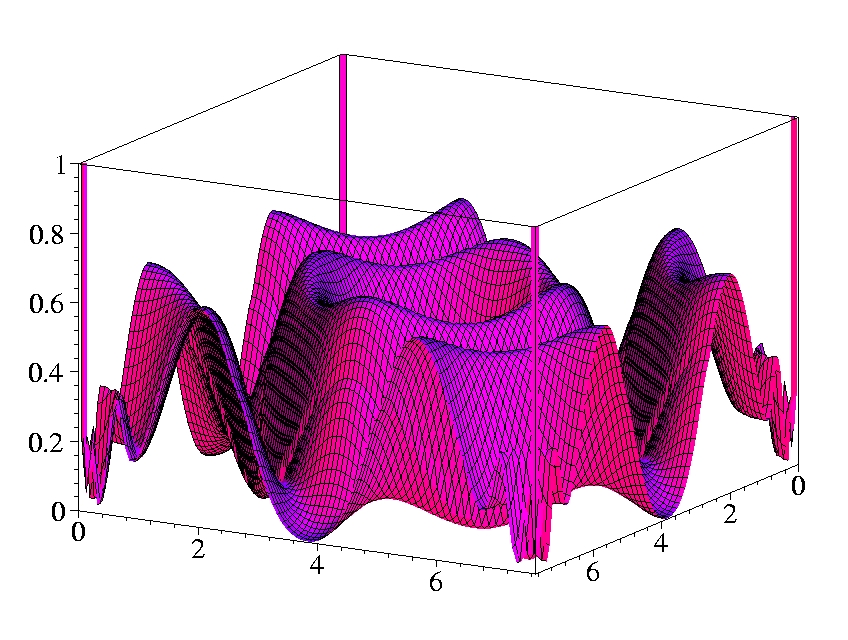
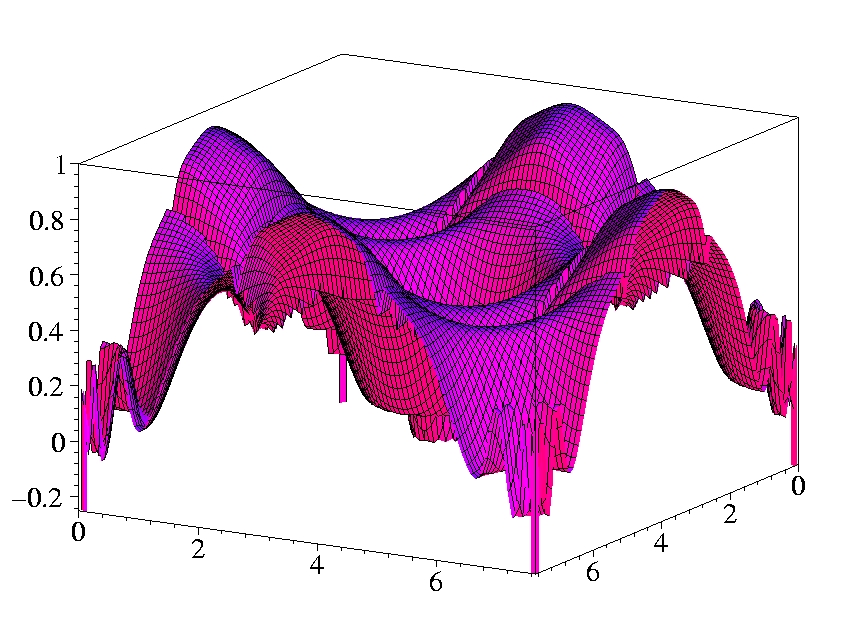
II.1) Oxygen
-
The plots show the gradients in the x-z-plane.
The atom is sitting on the x-axis at z = -1 Bohr.
-
The shell structure is obvious in both gradients.
-
The Laplacian of the density diverges at the position of the nucleus
(cusp condition).
-
Both gradients diverge for exponentially decaying density.
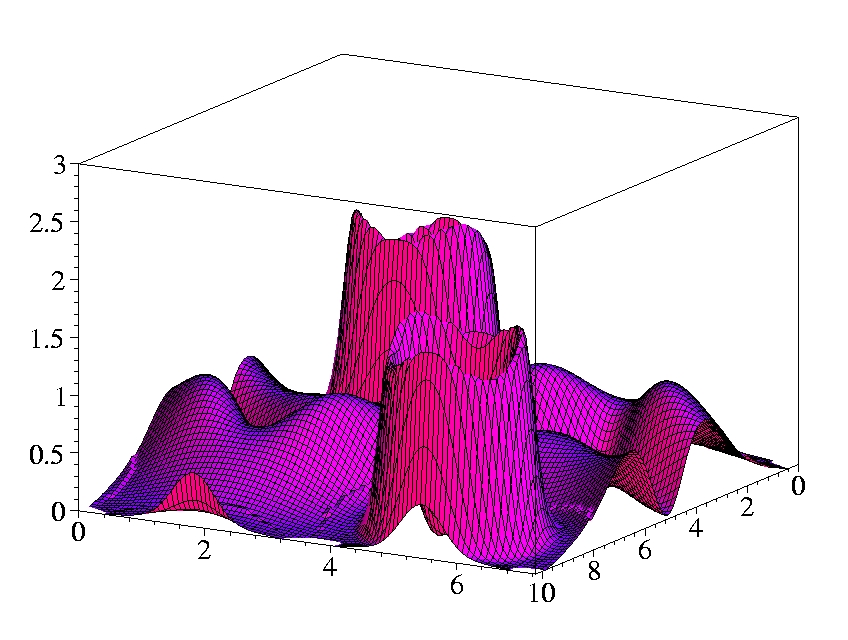
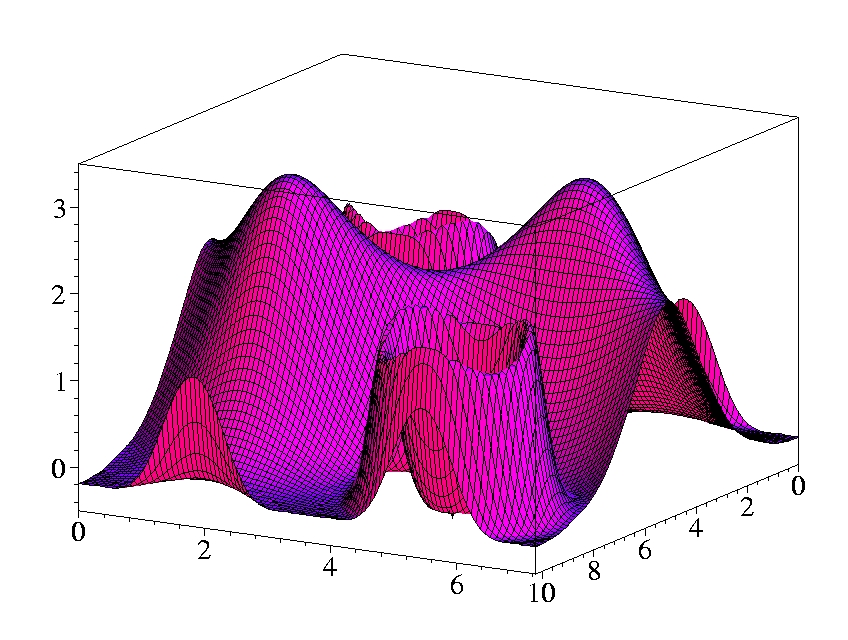
II.2) Chromium, Palladium, Radon
see
E. Engel and S. H. Vosko,
Phys. Rev. B 47, 13164 (1993).
III.1) H2
III.2) N2
IV.1) Silicon
IV.2) Gold
Home
Top
Last modified: April 13, 2004
Disclaimer
ee
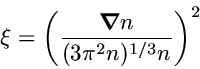
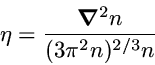
![E_x[n]](xieta/img3.png)