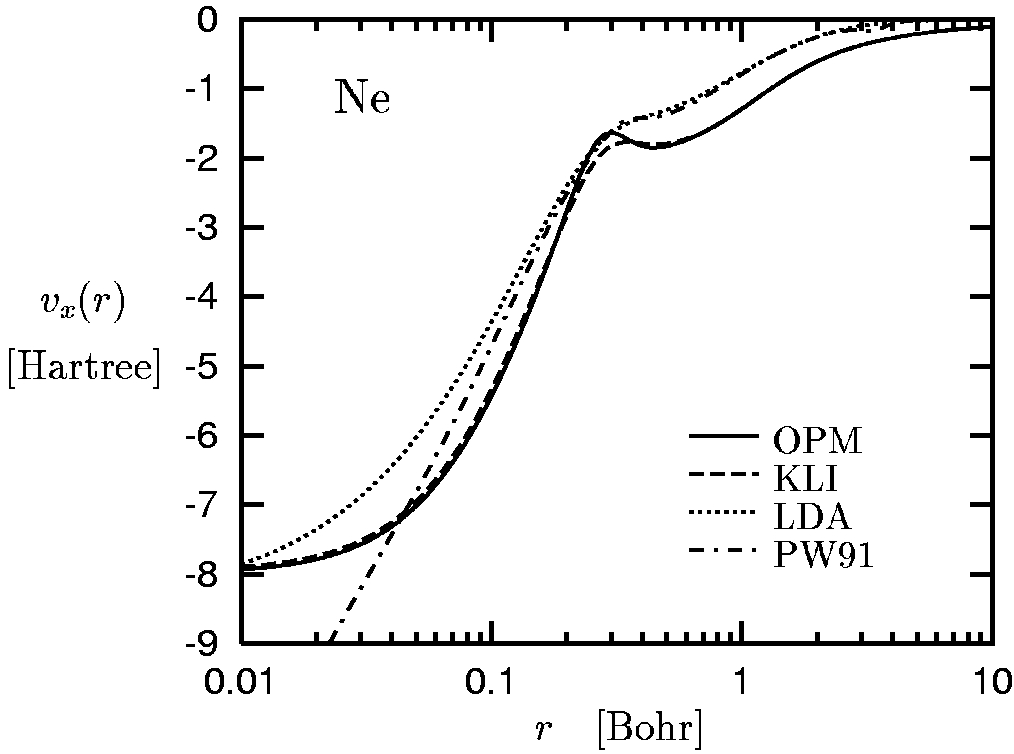
II.1) Neon (GGA = PW91 [3])

• The atomic shell structure is obvious in the exact exchange potential (OPM).
• The exact exchange potential falls off like -1/r for large r, i.e. in the asymptotic region in which the density decays exponentially.
• The KLI approximation also shows the shell structure, although much less pronounced. It is exact in the asymptotic regime.
• Neither the LDA nor the GGA reproduce the shell structure. The LDA and GGA potentials decay exponentially for large r (with the exception of the B88-GGA potential [4] which formally decays as r^-2 [5]).
• The GGA potential depends on the Laplacian of the density, which diverges like 1/r at the position of the nucleus (cusp condition).

II.2) Chromium, Palladium, Radon

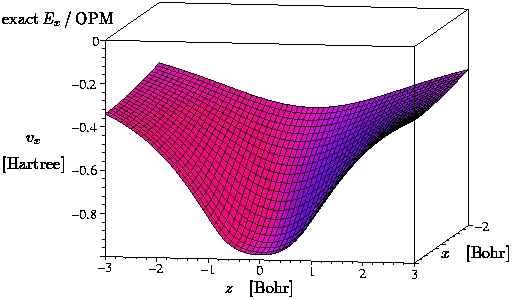
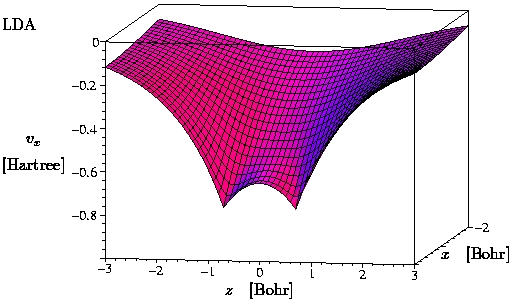
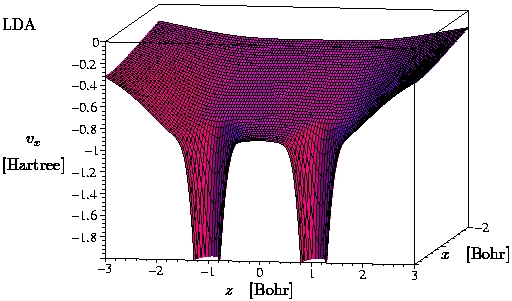
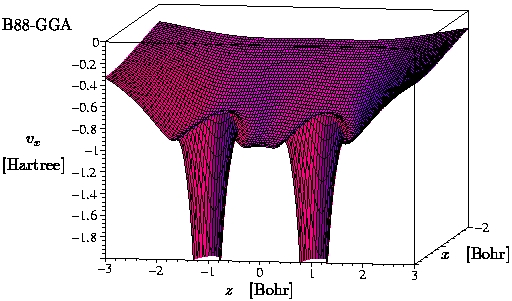
III.1) H₂ (GGA = B88 [4])

• The plots show the potential in the x-z-plane. The atoms are sitting on the x-axis at z = +/-0.7 Bohr.
• The exact exchange potential of H₂ only cancels the self-interaction component in the Hartree potential.

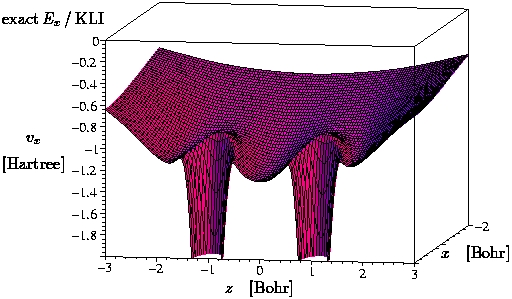
III.2) N₂ (GGA = B88 [4])

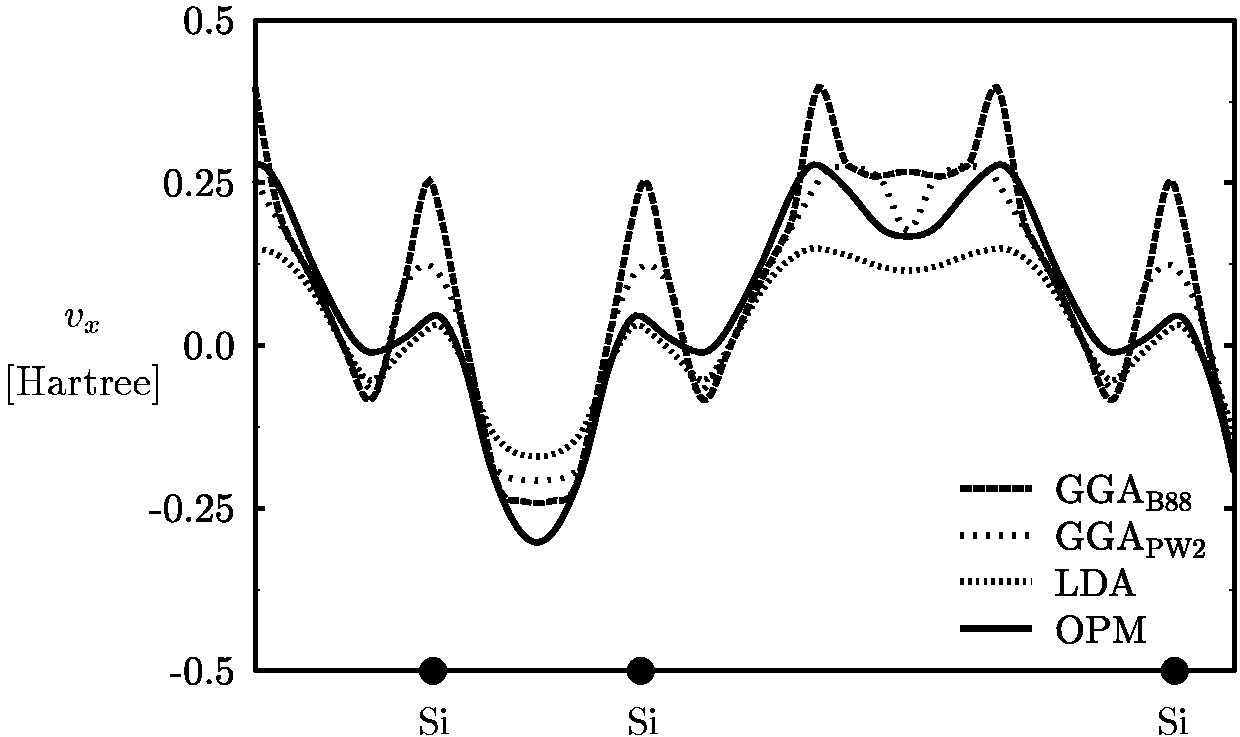
V.1) Silicon

• GGA = PW91 [3] and B88 [4]
• Plane-wave pseudopotential calculation with a cut-off energy of 25 Rydberg, k-point sampling based on 19 special k-points (a = 10.2 Bohr).
• The plots show the potential along [111] direction of the diamond structure.

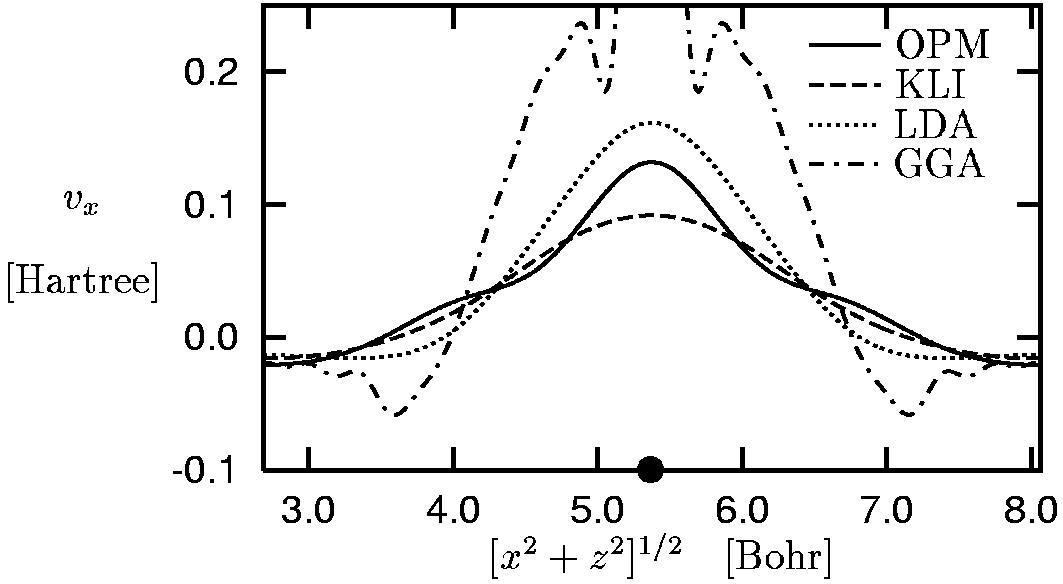
V.2) Aluminum

• GGA = PW91 [3]
• Plane-wave pseudopotential calculation with a cut-off energy of 100 Rydberg, k-point sampling based on 44 special k-points, 750 Kohn-Sham states included in evaluation of Kohn-Sham response function (a = 7.6 Bohr).
• The plots show the potential along [100] direction of the fcc structure.

• KLI approximation reasonably close to exact OPM result.
• GGA deviates much more from exact potential than LDA.