|
|
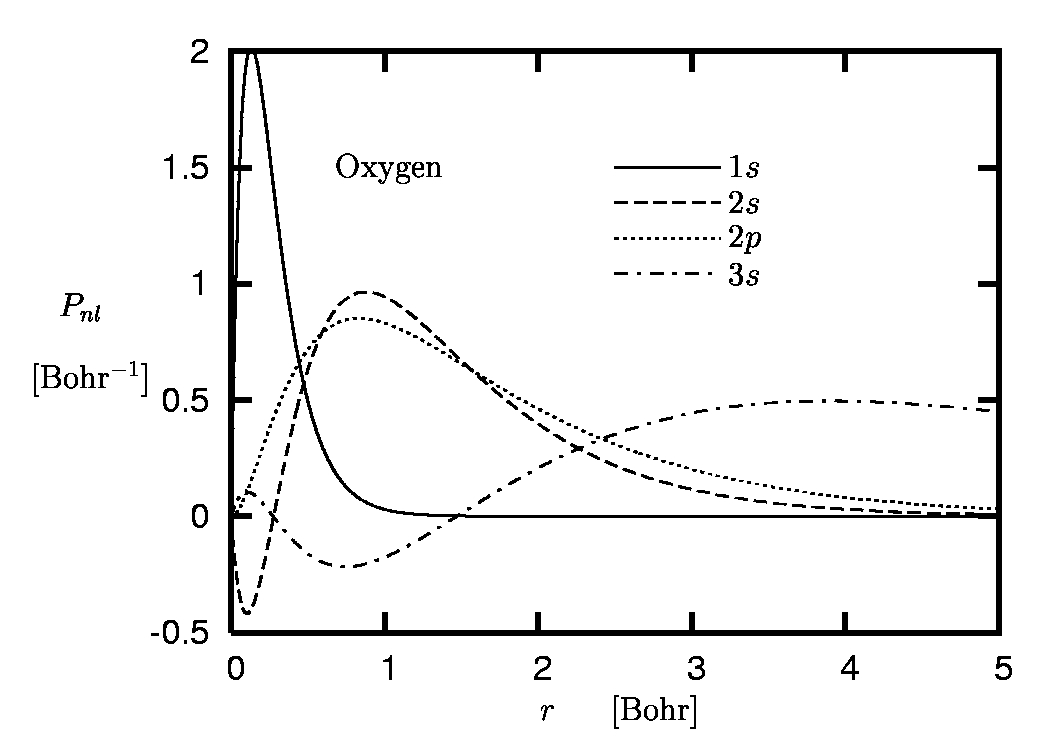
Figure 1:
Radial orbitals of oxygen:
Spatial separation of K-, L- and M-shell.
|
The main reason for the limited role of the core electrons in many processes is the spatial separation of the core and valence shells which originates from the comparatively strong binding of the core electrons to the nucleus. This effect is illustrated in Figure 1 where the radial orbitals Pnl of the oxygen atom are plotted.
One immediately recognizes the separation of the 1s-state with its r-expectation value of 0.2 Bohr from the L-shell orbitals with r-expectation values of roughly 1.2 Bohr. The corresponding eigenvalues differ by an order of magnitude. Similarly, the L-shell is well separated from the unoccupied M-shell orbitals. The spatial separation allows a clear decomposition of the complete spectrum into core, valence and higher-lying excited states.The interatomic distances in molecules or solids, however, are controlled by the spatial extension of the most weakly bound occupied orbitals. As a consequence, the much more localized core electrons have little overlap with the wavefunctions of electrons from neighboring atoms and thus essentially do not interact with them. They experience the presence of neighboring atoms only indirectly via the deformation of the valence orbitals. This repercussion, however, is rather weak due to the strong binding of the core states to the nucleus, so that the form of the core orbitals remains almost unchanged. There are only few situations in which the core states are directly affected by neighboring atoms, so that the PP concept breaks down. This is typically the case if charge centers are present and the core states are not sufficiently attracted by their own nucleus. The deformation of the 1s-orbital of lithium in LiF may serve as an example.
The precise decomposition of the bound state spectrum into core, valence and excited states is sometimes more difficult than for oxygen. From the arguments given above it is clear that problems will come up as soon as the spatial and/or energetic separation between two shells breaks down. This is, for instance, the case for the 3d transition metal elements, for which the most weakly bound 4s-state is not well-separated from the 3d-states. As a result the overlap of the 3d-orbitals with the orbitals from neighboring atoms is too large to be ignored. In this situation it is usually necessary to consider the complete shell, to which the critical d- or f-state belongs, as valence space, rather than just the critical state itself. These more strongly bound, but nevertheless relevant states are called semi-core states.
It is obvious that the quantum mechanical description of poly-atomic systems is simplified considerably if part of the spectrum is kept out of the calculation: As such calculations inevitably utilize some form of basis set for the representation of the wavefunctions, the computational effort is reduced substantially if only the valence states have to be expanded in terms of basis functions. The elimination of the core electrons and, at the same time, the small scale structure of the valence states allows the use of much smaller and much simpler basis sets, as the plane-wave basis usually employed in the context of quantum molecular dynamics. This is the basic idea behind the PP concept: Only the valence electrons are treated dynamically, i.e. represented by wavefunctions for which some Schrödinger-type equation is solved, while the core states are completely eliminated from the poly-atomic calculation. The presence of the core electrons, which essentially restrict the Hilbert space available to the valence electrons, must therefore be simulated by some other means, the pseudopotential: The orthogonality requirement is recast in the form of an effective potential. For each atom in the poly-atomic system there is a corresponding effective potential, responsible for representing the core states and the nucleus of this particular atom. The molecular or crystalline PP is then obtained by a linear superposition of the atomic PPs.
Ideally the atomic PP simply projects out all core states from the complete Fock space, while leaving the remaining spectrum unchanged. The exact formulation of such a projection potential is possible in principle, but the projection operators involved rely on an explicit representation of the core states. In the standard form of the PP approach the ambitions are thus cut back a little bit: Rather than requiring the PP to generate exactly the same atomic spectrum as the all-electron (AE) Hamiltonian (apart from the core states), one is satisfied with an accurate reproduction of just the valence states.
The term 'accurate reproduction' requires some explanation: Clearly, in the region of space in which most of the electronic norm is concentrated both orbitals must be very close, if not identical. On the other hand, the form of the valence orbitals in the core region, where the core electrons are moving, is less relevant: Otherwise the core states themselves would play a more important role. In the core region one can thus allow the pseudoorbital (PO) to differ from the all-electron orbital (AO) without loosing too much accuracy. In the case of our example, the oxygen atom, the core region roughly extends to 0.5 Bohr (see Figure 1).
Of course, one can not expect a single multiplicative PP to reproduce
several valence AOs, i.e. to simulate several projection operators
simultaneously.
In order to give this statement a more precise form one considers
some atomic valence shell n.
The standard form of the AOs is
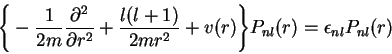
Given the AE information, the actual construction of the PPs proceeds in two steps. In the first step a screened radial PP vps,lsc is generated: vps,lsc is the total single-particle potential which has the desired pseudo valence state as lowest eigenstate. The identity of the pseudo with the AE orbital for r>rc,l requires the screened PP to coincide with the total AE Kohn-Sham (KS) potential in this valence region (as both orbitals satisfy the same radial differential equation). Consequently only the form of the PP in the core region remains to be determined. For the extension of the PP into the core region different procedures have been suggested [8-12] among which the Troullier-Martins (TM) approach [12] seems to be the most widely used. Compared with the orginal concept of Hamann, Schlüter and collaborators [8] the TM scheme produces somewhat smoother PPs, so that smaller plane-wave basis sets can be utilized in applications.
In the TM scheme an ansatz for the PO in the core region is made, which
|
|
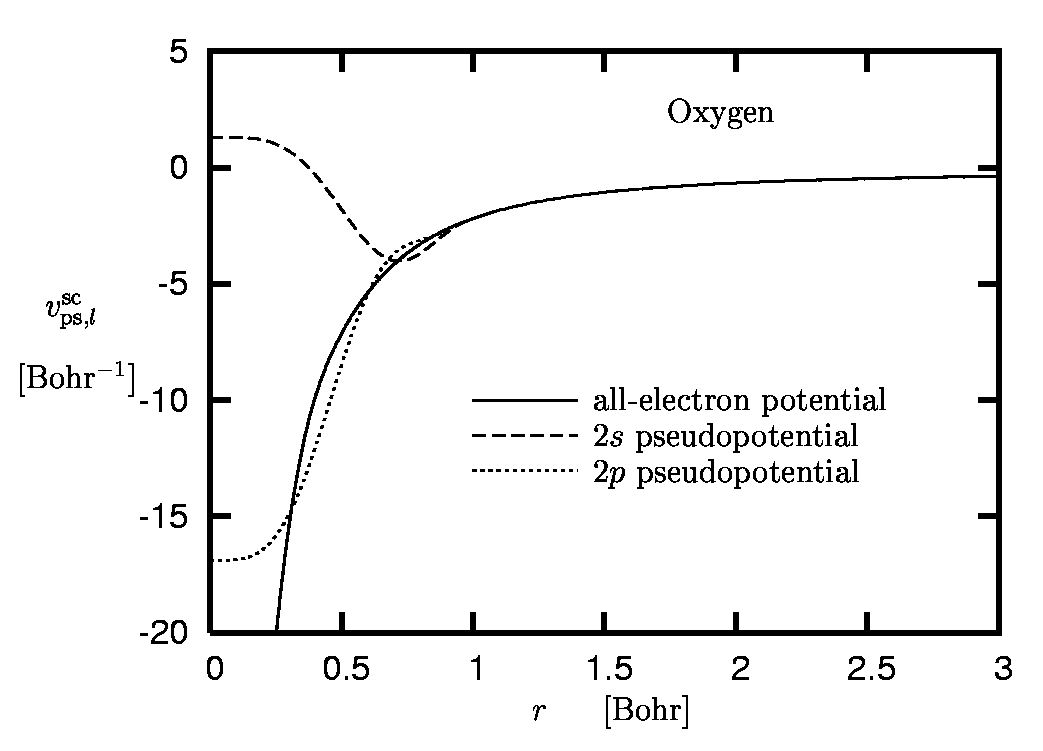
Figure 4:
Pseudopotential of oxygen:
Screened pseudopotentials versus all-electron potential.
As cut-off radii 1.0 Bohr and 0.9 Bohr have been used for the
2s and the 2p state, respectively.
|
In many cases the valence shell of an atom does not only consist of occupied states, but also contains unoccupied states. The most obvious example are the second row elements, for which the 3s and 3p orbitals are at least partially occupied, while the 3d orbital is empty. Unfortunately, the standard exchange-correlation (xc) functionals of DFT, the LDA and the GGA, do not yield bound 3d-levels for the ground state configurations of these atoms, as the corresponding xc-potentials decay exponentially for large r. One way to solve this problem is the use of a fractionally ionized configuration for the atom [8]: If the net positive charge on the atom is sufficiently large the critical orbital is bound. An alternative approach has been suggested by Hamann [11]. It is based on the observation that the actual form of the AE-orbital is only required for r<rc,l - for r>rc,l the PP is identical with the AE potential anyway. Moreover, the normalization of the orbital does not play any role for the final PP. The complete TM procedure can thus be carried through with any function obtained by outward-integration of the radial Kohn-Sham equations with the AE-potential, starting with appropriate boundary conditions at the origin. In the Hamann prescription one thus chooses some energy value in the appropriate range between the highest occupied KS state and zero and then performs an outward integration from 0 to some r-value beyond rc,l, using an arbitrary normalization. With the resulting function the standard procedure for the construction of the associated PP is gone through.
In a second step the interaction among the valence electrons (and their self-interaction) is eliminated from the screened PP by the so-called unscreening procedure. This step is required as PPs are usually applied to molecules or solids within a selfconsistent framework, typically nonrelativistic spin-density functional theory. In any non-perturbative framework, however, the differences between the atomic and the poly-atomic valence states are of crucial importance. The same is true for the interaction potentials between the valence states, most notably the direct electrostatic interaction. The screened PP contains the interaction among the atomic valence states, which is quite different from the interaction potential obtained with the molecular or bulk valence states. The atomic interaction potential must thus be eliminated from vps,lsc. The result is the unscreened PP which plays the role of the external potential in the poly-atomic calculation, analogous to the nuclear potential in the AE situation.
The simplest approach for this elimination is linear unscreening,
![\begin{eqnarray*}
v_{\rm H}([n];r)
&=&
4\pi e^2
\Bigg\lbrace
{1\over r} \int_0^r...
..._{\rm xc}([n];r)
&=&
{\delta E_{\rm xc}[n]\over\delta n(\bm{r})}
\end{eqnarray*}](ncpp/img129.png)
Linear unscreening provides a complete elimination of the direct Coulomb interaction among the valence electrons, as the Hartree potential is linear in the density. The xc-energy functional Exc of DFT, on the other hand, is a nonlinear functional of the density. Linear unscreening thus implies a linearization of Exc with respect to the core-valence interaction. The quality of the linearization obviously depends on the spatial overlap between the core density and the valence xc-potential. In the case of the (semi-)local functionals LDA and GGA this overlap is directly determined by the overlap of core and valence density, which is nonzero only in the transition region between valence and core shells. The overlap does not vanish completely even for first row elements (compare Figure 1), so that the nonlinearity of Exc shows up even for these ideal PP candidates. Nevertheless, linear unscreening is often sufficient, at least as long as the accuracy requirements are not particularly high.
The nonlinearity of Exc can be
taken into account via the so-called nonlinear core corrections
(nlccs) [13].
In this approach the atomic core density
nc
is included in the xc-component of the unscreening potential,
so that the complete atomic core-valence interaction is eliminated.
As a consequence nc
must then be added to the valence density of the poly-atomic system
when the xc-potential of this system is calculated.
Fortunately, one needs only that part of
nc which actually
has overlap with the valence density.
This allows a smooth truncation of
nc
below some core-cut-off radius
rnlcc.
The unscreened PP including nlccs is then given by
The example of oxygen is given in Figure 5. One immediately observes the different asymptotics, reflecting the fact that vps,l asymptotically approaches -Zion/r, while the screened PP has the same behavior as the AE potential (which falls off like -1/r on the exact level and decays exponentially within the standard approximations of DFT).
So far, the formulation of PPs has been strictly nonrelativistic, so
that the issue of heavy elements still remains to be addressed.
In fact, the PP treatment is particularly attractive for heavy atoms
for which many shells belong to the core states.
In order to cover the complete periodic table the PP construction is
thus usually based on relativistic AE results
[14].
This leads to j-dependent PPs
vps,lj, in accordance
with the j-dependence of the individual valence states.
However, while the core states directly experience the relativistic
effects, the valence states are in most cases only indirectly affected
by relativity via the orthogonality requirement (which is simulated by
the PP).
Consequently, poly-atomic PP calculations are usually performed in
a nonrelativistic framework, even if heavy ions are present.
The j-independent PPs required for these nonrelativistic
calculations are then obtained from a j-average,
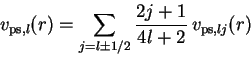
In order to address this question one has to analyze the sensitivity of the agreement between atomic POs and AOs to the specific eigenenergy in the single-particle equation. One finds that the variation of the logarithmic derivative P'nl(r)/Pnl(r) with the single-particle energy is determined by the norm contained in the sphere between the origin and r. This is true in particular in the neighborhood of one of the actual atomic eigenvalues εnl, i.e. for a bound atomic eigenstate. Thus, as soon as norm-conservation is ensured, the POs exactly reproduce the energy dependence of the logarithmic derivative of the AOs for r>rc,l. Consequently, one expects the POs to react as the AOs when the valence states experience some energy shift in a poly-atomic environment -- provided the underlying PPs are norm-conserving. This argument supporting the transferability of PPs emphasizes the importance of norm-conservation in a very explicit way.
In practice, it is nevertheless always recommendable to check the
transferability explicitly by examination of some suitable atomic
excitation process and of the binding properties of simple molecular
or crystalline systems.
| rc,l [Bohr] | rnlcc | |||
| s | p | d | [Bohr] | |
| Li | 2.8 | 3.0 | -- | 1.2 |
| Be | 1.7 | 1.5 | -- | 0.7 |
| B | 1.3 | 1.3 | -- | 0.6 |
| C | 1.2 | 1.1 | -- | 0.4 |
| N | 1.1 | 1.0 | -- | 0.3 |
| O | 1.0 | 0.9 | -- | 0.25 |
| F | 0.6 | 0.5 | -- | 0.2 |
| Na | 2.7 | 2.7 | 2.7 | 2.0 |
| Mg | 1.9 | 2.3 | 2.3 | 1.2 |
| Al | 1.9 | 2.3 | 2.3 | 1.0 |
| Si | 1.8 | 2.0 | 2.0 | 1.0 |
| P | 1.7 | 1.7 | 1.7 | 0.8 |
| S | 1.4 | 1.5 | 1.5 | 0.7 |
| Cl | 1.2 | 1.2 | 1.2 | 0.6 |
| rc,l [Bohr] | Re | De | ωe | |
| s | p | [Bohr] | [eV] | [cm-1] |
| 1.1 | 1.0 | 2.065 | 10.967 | 2381 |
| 1.3 | 1.2 | 2.068 | 10.935 | 2371 |
| 1.5 | 1.4 | 2.073 | 10.827 | 2342 |
The second quality parameter of interest is the truncation radius of
the core density, required for nlccs.
The truncated core density nps,c
becomes more and more strongly peaked, the smaller
rnlcc is chosen.
The spacing of the spatial grid in poly-atomic calculations, however,
is often too low to resolve this small-scale structure
of nps,c.
A smaller rnlcc thus requires
a finer grid, which means a higher energy cut-off in the case of
plane-wave basis sets.
This effect is demonstrated in Table 3.
| cut-off | results | ||||
| Emax = Gmax2 / (2m) | π/ (2Gmax) | -Etot(N) | Re | De | ωe |
| [Rydberg] | [Bohr] | [Hartree] | [Bohr] | [eV] | [cm-1] |
| without nlccs | |||||
| 50 | 0.22 | 9.669 | 2.085 | 10.508 | 2348 |
| 100 | 0.16 | 9.749 | 2.065 | 10.830 | 2354 |
| 200 | 0.11 | 9.751 | 2.065 | 10.830 | 2354 |
| 400 | 0.08 | 9.751 | 2.065 | 10.830 | 2354 |
| with nlccs | |||||
| 50 | 0.22 | 12.662 | 2.009 | 1.805 | 2154 |
| 100 | 0.16 | 12.197 | 2.060 | 10.452 | 2386 |
| 200 | 0.11 | 12.147 | 2.067 | 11.262 | 2368 |
| 400 | 0.08 | 12.142 | 2.067 | 11.346 | 2368 |
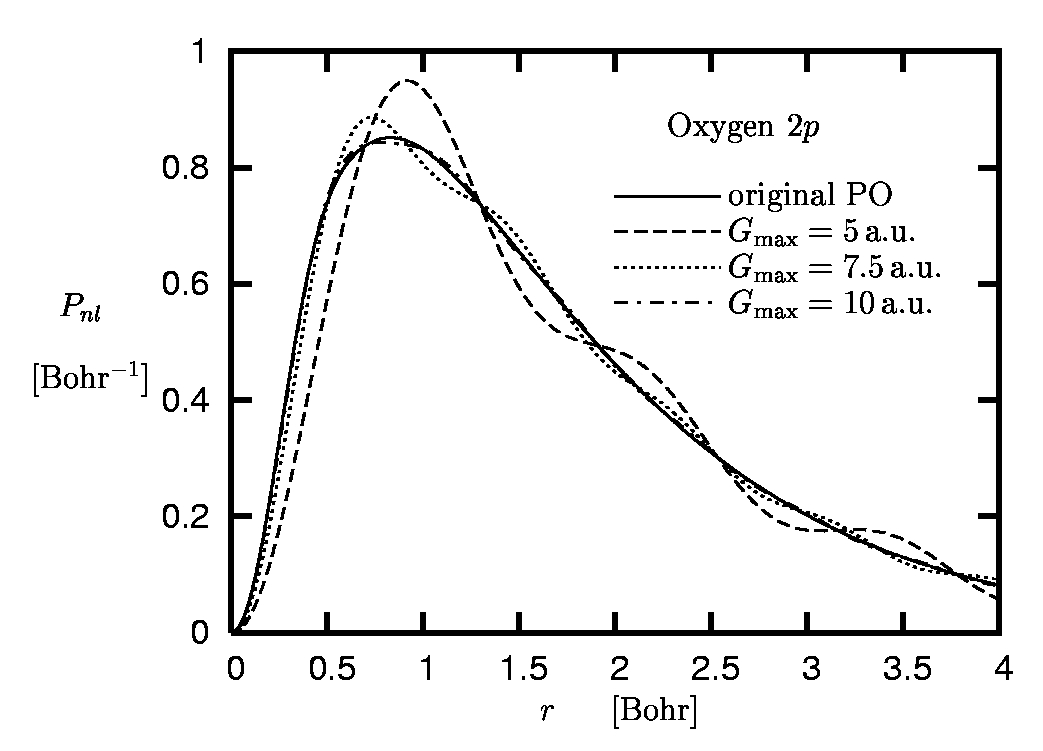
The convergence properties can also be analyzed from a different perspective. In the standard plane-wave pseudopotential scheme the Fourier representation of the POs is truncated at some cut-off momentum Gmax. This truncated Fourier transform deviates from the original PO. The difference between the truncated Fourier and the original PO is illustrated in Figure 6 for the case of the 2p-state of oxygen.
|
|
Figure 6:
Radial 2p orbital of oxygen:
Original pseudoorbital versus Fourier
representations obtained for different cut-off momenta
Gmax.
|
|
|
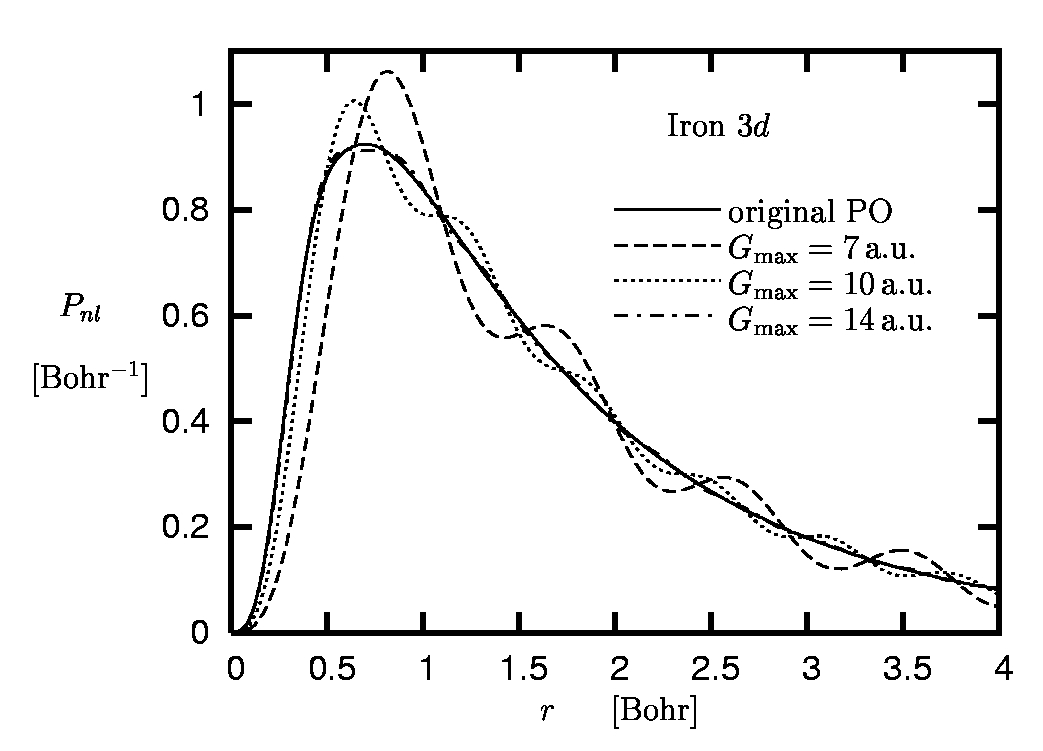
Figure 7:
Radial 3d orbital of iron:
Original pseudoorbital versus Fourier
representations obtained for different cut-off momenta
Gmax
(rc,3d = 0.8 Bohr).
|
All calculations are based on the LDA for the xc-functional, using the parametrization of Vosko, Wilk and Nusair [16]. In order to be consistent with the nonrelativistic AE data, both the PP construction and all calculations are strictly nonrelativistic. Whereever present, spin-polarization is taken into account.
The first class of results which is of interest in this context are
excitation energies.
In Table 4 we list the s-p transfer energies of first
and second row atoms.
All calculations utilize spherically averaged densities.
| atom | ns↓ → np↑ | ns↓ → np↓ | ||||
| AE | PP | PP+nlcc | AE | PP | PP+nlcc | |
| Be | 2.47 | 2.37 | 2.46 | 3.49 | 3.49 | 3.49 |
| B | 3.23 | 3.00 | 3.21 | 5.57 | 5.57 | 5.56 |
| C | 4.05 | 3.68 | 4.01 | 8.02 | 8.02 | 8.00 |
| N | 10.86 | 10.87 | 10.84 | |||
| O | 14.38 | 14.39 | 14.37 | |||
| F | 18.22 | 18.24 | 18.22 | |||
| Mg | 2.80 | 2.69 | 2.80 | 3.44 | 3.40 | 3.44 |
| Al | 3.61 | 3.41 | 3.61 | 5.01 | 4.96 | 5.01 |
| Si | 4.31 | 3.98 | 4.29 | 6.57 | 6.48 | 6.57 |
| P | 8.14 | 8.02 | 8.14 | |||
| S | 9.95 | 9.89 | 9.95 | |||
| Cl | 11.79 | 11.76 | 11.78 | |||
As a third example we consider molecular ground state properties.
The spectroscopic constants obtained for first row diatomic molecules
are listed in Table 5.
| mode | Re | De | ωe | |
| [Bohr] | [eV] | [cm-1] | ||
| B2 | AE | 3.032 | 3.855 | 1042 |
| 3Σ | PP | 3.023 | 3.790 | 1037 |
| PP+nlcc | 3.034 | 3.852 | 1040 | |
| C2 | AE | 2.353 | 7.251 | 1890 |
| 1Σ | PP | 2.350 | 6.923 | 1877 |
| PP+nlcc | 2.355 | 7.223 | 1885 | |
| N2 | AE | 2.068 | 11.593 | 2390 |
| 1Σ | PP | 2.065 | 10.967 | 2381 |
| PP+nlcc | 2.068 | 11.494 | 2387 | |
| O2 | AE | 2.273 | 7.591 | 1626 |
| 3Σ | PP | 2.279 | 7.240 | 1613 |
| PP+nlcc | 2.279 | 7.506 | 1612 | |
| F2 | AE | 2.614 | 3.397 | 1062 |
| 1Σ | PP | 2.619 | 3.234 | 1058 |
| PP+nlcc | 2.618 | 3.375 | 1059 | |
| LiH | AE | 3.032 | 2.643 | 1375 |
| 1Σ | PP | 2.917 | 2.720 | 1320 |
| PP+nlcc | 3.037 | 2.597 | 1322 | |
| CO | AE | 2.128 | 12.967 | 2183 |
| 1Σ | PP | 2.125 | 12.589 | 2164 |
| PP+nlcc | 2.128 | 12.900 | 2181 | |
| average | PP | 0.026 | 0.235 | 15 |
| deviation | PP+nlcc | 0.003 | 0.044 | 12 |
Table 5 documents the well-known success of norm-conserving PPs. Even without nlccs the average error in the bond length is no larger than 0.03 Bohr. This deviation is reduced to less than 0.01 Bohr by inclusion of nlccs. The nlccs are somewhat more important for the dissociation energy. Although the average error of 0.24 eV found for the first row molecules without nlccs is sufficient for many purposes, it is not completely satisfactory. This error mainly originates from molecules whose constituents are ``strongly'' spin-polarized, with Nitrogen being the prime example. For these systems the dissociation energy is generally underestimated without nlccs, as a consequence of an overestimation of the atomic ground state energy. This is consistent with the observation that quite generally the energy of high-spin states is overestimated by PPs without nlccs. These difficulties are resolved by inclusion of nlccs: The resulting average error of 0.05 eV is much smaller than the level of accuracy which can be achieved in calculations for more complex molecules.
As pointed out earlier, the PP-treatment of
transition metal elements is complicated by the large overlap of
the (n-1)d orbital with the ns orbital.
In this case it is necessary to include the semi-core states in the
valence space, if fully reliable results are desired.
The success of this procedure is demonstrated in Table 6
in which the spectroscopic constants for some diatomic molecules
containing transition metal elements are listed.
| mode | Re | De | ωe | |
| [Bohr] | [eV] | [cm-1] | ||
| Fe2 | PP | 3.68 | 3.91 | 440 |
| 7Δ | PP+nlcc | 3.68 | 4.31 | 440 |
| AE | 3.68 | 4.38 | 497 | |
| Ni2 | PP | 3.85 | 3.56 | 363 |
| 3Σ | PP+nlcc | 3.85 | 3.49 | 362 |
| AE | 3.87 | 3.64 | 354 | |
| FeO | PP | 2.99 | 6.65 | 962 |
| 5Δ | PP+nlcc | 2.99 | 7.00 | 968 |
| AE | 3.01 | 7.06 | 957 | |
| CrO | PP | 3.01 | 6.06 | 952 |
| 5Π | PP+nlcc | 2.99 | 6.38 | 978 |
| AE | 3.02 | 6.15 | 976 |
In order to illustrate the accuracy of the charge densities
resulting from PP calculations, the dipole moment of diatomic FeO
is considered in Table 7.
| R | AE | PP |
| [Bohr] | [Debye] | |
| 2.90 | 3.92 | 3.93 |
| 3.00 | 4.27 | 4.29 |
| 3.10 | 4.59 | 4.61 |
Finally, in Table 8 some exemplary results for the
cohesive properties of metals and semiconductors are given.
| system | mode | a | Ecoh | B | M |
| [Bohr] | [eV/atom] | [GPa] | [μB/atom] | ||
| Na | AE [18] | 7.65 | 9.2 | ||
| PP [19] | 7.52 | 1.28 | 8.7 | ||
| PP+nlcc [19] | 7.65 | 1.22 | 9.1 | ||
| Al | AE [18] | 7.52 | 84 | ||
| PP | 7.47 | 4.08 | 86 | ||
| PP+nlcc | 7.48 | 4.08 | 88 | ||
| Fe | AE (rel.) | 5.21 | 266 | 2.08 | |
| (bcc) | PP (rel.) | 5.21 | 6.36 | 276 | 2.15 |
| PP+nlcc (rel.) 400/26 | 5.18 | 6.63 | 192 | 1.97 | |
| Si | AE [18] | 10.22 | 5.28 | 96 | |
| PP [19] | 10.17 | 5.34 | 94 | ||
| PP+nlcc [19] | 10.19 | 5.32 | 94 | ||
| Ge | AE [18] | 10.63 | 4.54 | 78 | |
| PP [19] | 10.51 | 4.75 | 73 | ||
| PP+nlcc [19] | 10.58 | 4.58 | 71 | ||
| GaAs | AE [18] | 10.62 | 7.99 | 74 | |
| PP [19] | 10.39 | 8.68 | 79 | ||
| PP+nlcc [19] | 10.53 | 8.15 | 75 |
The long-range structure thus has to be damped which is most easily
done by multiplication of the unscreened PP with some damping
function [21].
However, any a posteriori damping of the unscreened PP
introduces additional parameters for which no physically motivated
values are available.
In fact, suitable choice of the damping parameters allows to generate
essentially any desired result for poly-atomic systems [17].
A systematic scheme for the elimination of the long-range structure
has been suggested by our group [17].
In this scheme a parameter-free, self-consistent procedure based on
the standard norm-conserving PPs is utilized for the PP construction.
With these asymptotically correct PPs the quality of PP results
obtained with the exact exchange is as high as that of the
corresponding LDA PP data [17].
As an illustration Table 9 lists the spectroscopic constants of the same
first row diatomic molecules as shown in Table 5.
| mode | Re | De | ωe | |
| [Bohr] | [eV] | [cm-1] | ||
| Li2 | AE | 5.266 | 0.168 | 338 |
| PP | -0.004 | 0.001 | -1 | |
| SC-PP | -0.009 | 0.003 | -1 | |
| B2 | AE | 3.068 | 0.608 | 972 |
| PP | 0.006 | -0.028 | -5 | |
| SC-PP | -0.005 | 0.046 | 0 | |
| C2 | AE | 2.332 | 0.281 | 1933 |
| PP | -0.001 | 0.173 | 7 | |
| SC-PP | -0.009 | 0.098 | 6 | |
| N2 | AE | 2.011 | 4.972 | 2736 |
| PP | -0.003 | 0.381 | 24 | |
| SC-PP | -0.008 | 0.170 | 13 | |
| O2 | AE | 2.184 | 1.441 | 1981 |
| PP | -0.017 | 0.365 | 66 | |
| SC-PP | -0.002 | 0.025 | -10 | |
| F2 | AE | 2.496 | -1.607 | 1283 |
| PP | -0.034 | -0.097 | 63 | |
| SC-PP | 0.002 | -0.034 | -2 | |
| LiH | AE | 3.037 | 1.483 | 1427 |
| PP | 0.028 | -0.036 | -37 | |
| SC-PP | 0.000 | -0.022 | -34 | |
| FH | AE | 1.694 | 4.203 | 4501 |
| PP | 0.001 | -0.014 | -16 | |
| SC-PP | 0.000 | -0.040 | -22 | |
| CO | AE | 2.080 | 7.530 | 2444 |
| PP | -0.002 | 0.262 | 16 | |
| SC-PP | -0.009 | 0.162 | 12 | |
| average | PP | 0.011 | 0.150 | 26 |
| deviation | SC-PP | 0.005 | 0.067 | 11 |
| mode | a | Ecoh | B |
| [Bohr] | [eV/atom] | [GPa] | |
| PP | 7.10 | 3.98 | 135 | SC-PP | 7.79 | 1.37 | 71 |
| AE-LDA | 7.52 | 84 | |
| Expt. | 7.65 | 3.39 | 77 |
Last modified: April 19, 2004
Disclaimer
ee