Density Functional Theory
Home
|
|
|
|
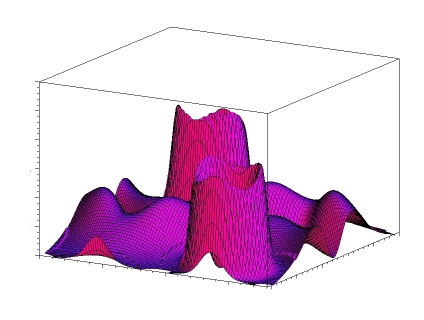
Characteristic density gradient for Silicon (dia)
|
Density Functional Theory (DFT) is a general approach to the ab
initio description of quantum many-particle systems, in which
the original many-body problem is rigorously recast in the form of
an auxiliary single-particle problem (for an overview see [1]).
For the most simple case of (nondegenerate) stationary problems,
DFT is based on the fact that any ground state observable is uniquely
determined by the corresponding ground state density n, i.e.
can be understood as a functional of n.
This statement in particular applies to the ground state energy,
which allows a representation of the particle-particle interaction
effects in an indirect form via a density-dependent single-particle
potential.
In addition to the Hartree (direct) contribution, this potential
contains an exchange-correlation (xc) component, which is obtained
from the so-called xc-energy functional.
The exact density functional representation of this crucial quantity
of DFT is not known, the derivation of suitable approximations being
the major task in DFT.
Extensions of this scheme to relativistic [2] and time-dependent [3]
systems, utilizing the four current and the time-dependent density as
basic variables, are also available.
Furthermore, a DFT approach to quantum hadrodynamics (as a model
for the relativistic description of nuclei) has been developed [4].
The main areas for applications of DFT are condensed matter and
cluster physics as well as quantum chemistry.
Our research focuses on the development of more accurate density
functional methods and a deeper understanding of the foundations
of relativistic DFT.
Applications to critical classes of systems (like van-der-Waals
bond molecules or Mott insulators) serve as a test of new functionals.
In addition, density functional methods are used to study the
structure and dynamics of molecules, clusters and solids.
-
E. Engel and R. M. Dreizler,
Density Functional Theory: An Advanced Course,
(Springer, Berlin, 2011);
-
E. Engel,
in: Relativistic Electronic Structure Theory,
Part 1. Fundamentals,
edited by P. Schwerdtfeger
(Elsevier, Amsterdam, 2002), p.524-624.
-
E. K. U. Gross, J. F. Dobson, and M. Petersilka,
Top. Curr. Chem. 181, 81 (1996).
-
C. Speicher, R. M. Dreizler, and E. Engel,
Ann. Phys. (N.Y.) 213, 312 (1992).
Home
Top
Last revision: Nov 15, 2009
Disclaimer
ee

