Density Functional Calculations for Amino Acids

• Brief introduction
• Ground states and low-lying conformers of glycine, alanine and serine
• References

I) Brief introduction

• the representation of the ionic cores by normconserving pseudopotentials (applying the Troullier-Martins form [3] and the Kleinman-Bylander transformation [4]),
• a plane-wave expansion of the single-particle Kohn-Sham states,
• the supercell concept for periodic repetition of the molecules (using a simple cubic unit cell),
• the local density approximation (in the VWN parameterization [5]) or the generalized gradient approximation (in the PW form [6]) for the exchange-correlation energy functional,
• a quasi-Newton method for the relaxation of the ionic positions, i.e. the total energy minimization (Broyden-Fletcher-Goldfarb-Shanno algorithm).

• the basis set size -- in the case of plane-wave basis sets this size is determined by the highest energy present in the basis, the cut-off energy --
• and the size of the supercell, which has to make sure that the neighboring molecules do not interact.

The results can be summarized as follows:

• The structures of all low-lying conformers examined in this work are obtained rather accurately by density functional methods.
• The same is not true for the energetic ordering of the various states: The subtle energy differences involved can not always be reproduced by the LDA or GGA, indicating the limitations of these (semi)local functionals.
• Gradient corrections appear to be less important for these organic molecules than for many solids.
• The calculations demonstrate the feasibility of DFT calculations for comparatively complex systems on present day consumer PC's.

II) Results for Glycine

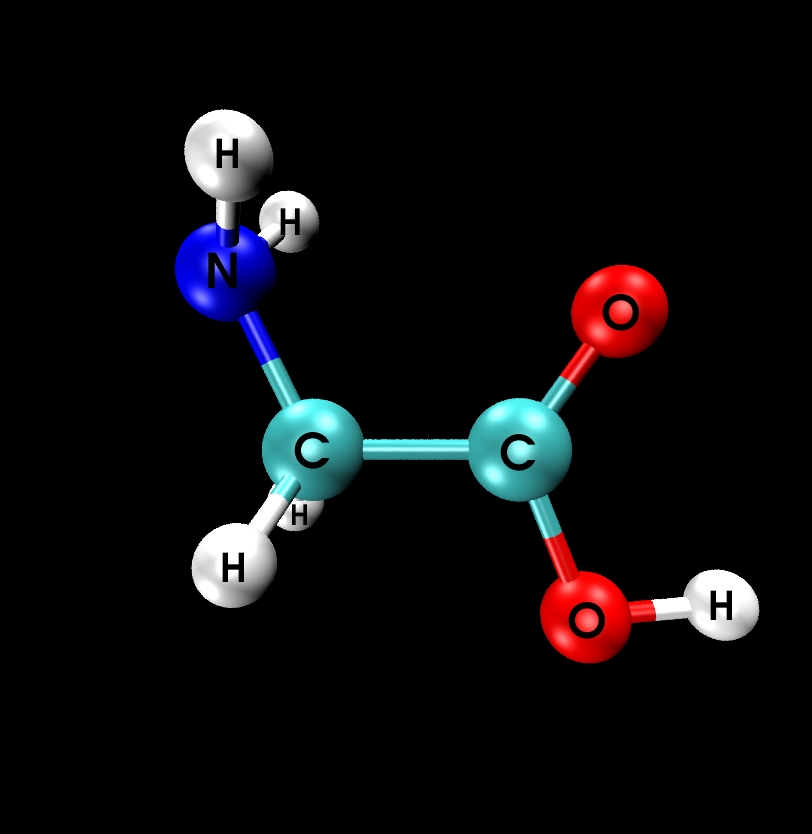
II.1) Ground state: Glycine Ip (planar)

Calculational parameters xc-functional LDA [5] cut-off energy 100 Rydberg pseudopotential Troullier-Martins [3] nonlinear core corrections no supercell size 23 Bohr Results bond lengths [Angstroms] bond angles [degrees] bond expt. [9] LDA angle expt. [9] LDA N-H (1.001) 1.020 H-N-H (110.3) 106.5 N-C 1.467 1.431 H-N-C (113.3) 111.0 C-H (1.081) 1.101 N-C-C 112.1 115.9 C-C 1.526 1.506 H-C-H (107.0) 104.4 C-O 1.355 1.332 C-C-O 111.6 114.9 C=O 1.205 1.200 C-C=O 125.1 125.7 O-H (0.966) 0.976 C-O-H (112.3) 104.7 experimental results in brackets are based on estimates reasonable agreement between LDA and experiment however: LDA erroneously predicts conformer IIp to be energetically lower than the Ip state by 0.14 eV

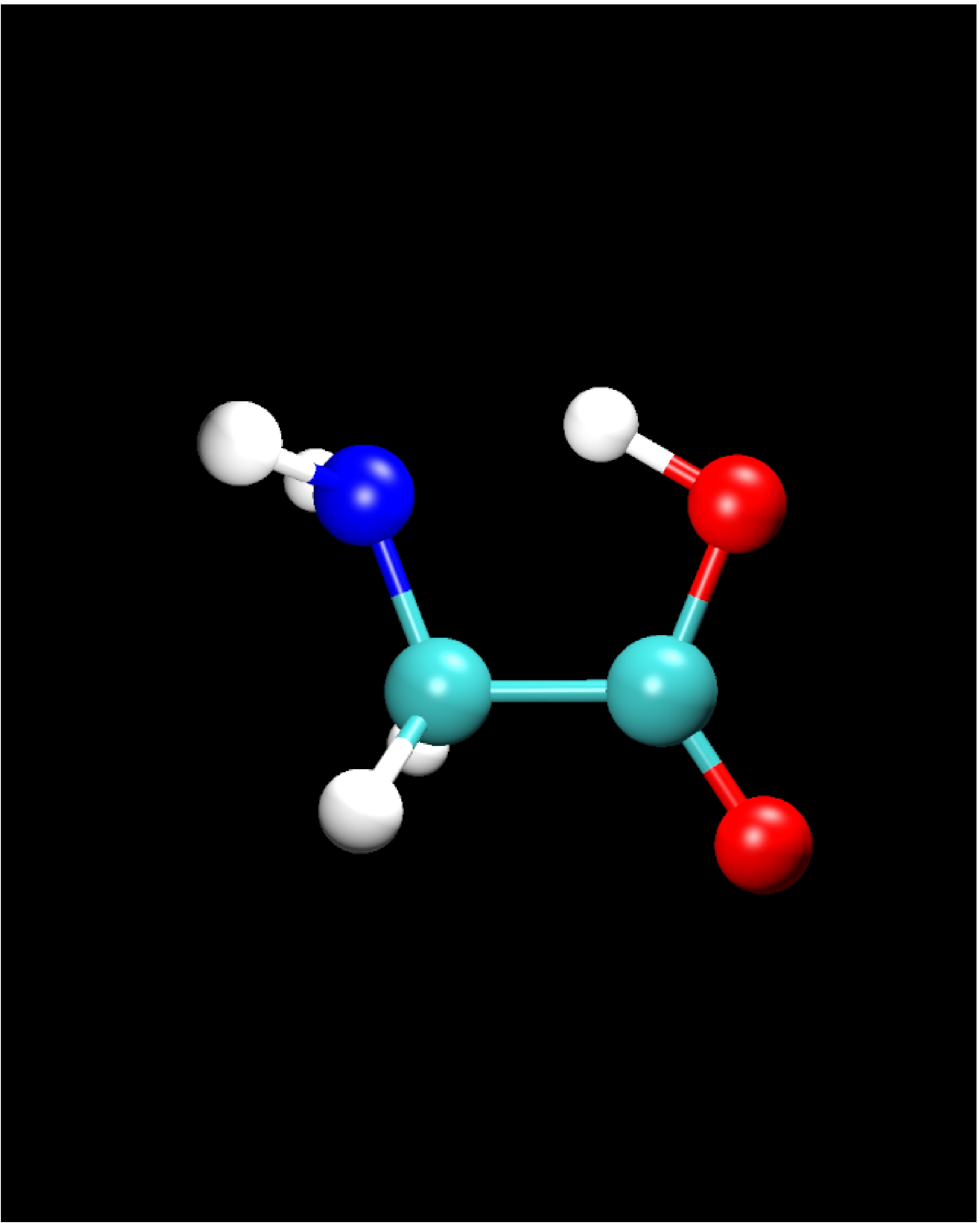
II.2) Energetically lowest conformer: Glycine IIp

Calculational parameters xc-functional LDA [5] cut-off energy 60 and 100 Rydberg pseudopotential Troullier-Martins [3] nonlinear core corrections no supercell size 23 Bohr Results bond lengths [Angstroms] bond angles [degrees] bond LDA 60 Ryd LDA 100 Ryd angle LDA 60 Ryd LDA 100 Ryd N-H 1.026 1.019 H-N-H 107.9 108.7 N-C 1.453 1.449 H-N-C 113.1 113.7 C-H 1.103 1.099 N-C-C 109.9 110.4 C-C 1.518 1.518 H-C-H 106.2 106.1 C-O 1.338 1.324 C-C-O 112.2 112.0 C=O 1.228 1.203 C-C=O 122.5 123.1 O-H 1.046 1.023 C-O-H 100.0 101.8 A bond contraction is observed, when increasing the basis set size from 60 to 100 Rydberg: The oxygen bonds are affected most strongly. Results for 80 Rydberg are almost identical with those for 100 Rydberg.

Calculational parameters xc-functional GGA [6] cut-off energy 80 Rydberg pseudopotential Troullier-Martins [3] nonlinear core corrections no supercell size 23 Bohr Results bond lengths [Angstroms] bond angles [degrees] bond GGA angle GGA N-H 1.013 H-N-H 107.9 N-C 1.453 H-N-C 112.8 C-H 1.088 N-C-C 110.5 C-C 1.518 H-C-H 106.4 C-O 1.344 C-C-O 112.8 C=O 1.224 C-C=O 122.7 O-H 1.020 C-O-H 101.1 GGA contracts bonds slightly compared to LDA: Effect of gradient corrections is less dramatic than for many inorganic molecules and for solids.

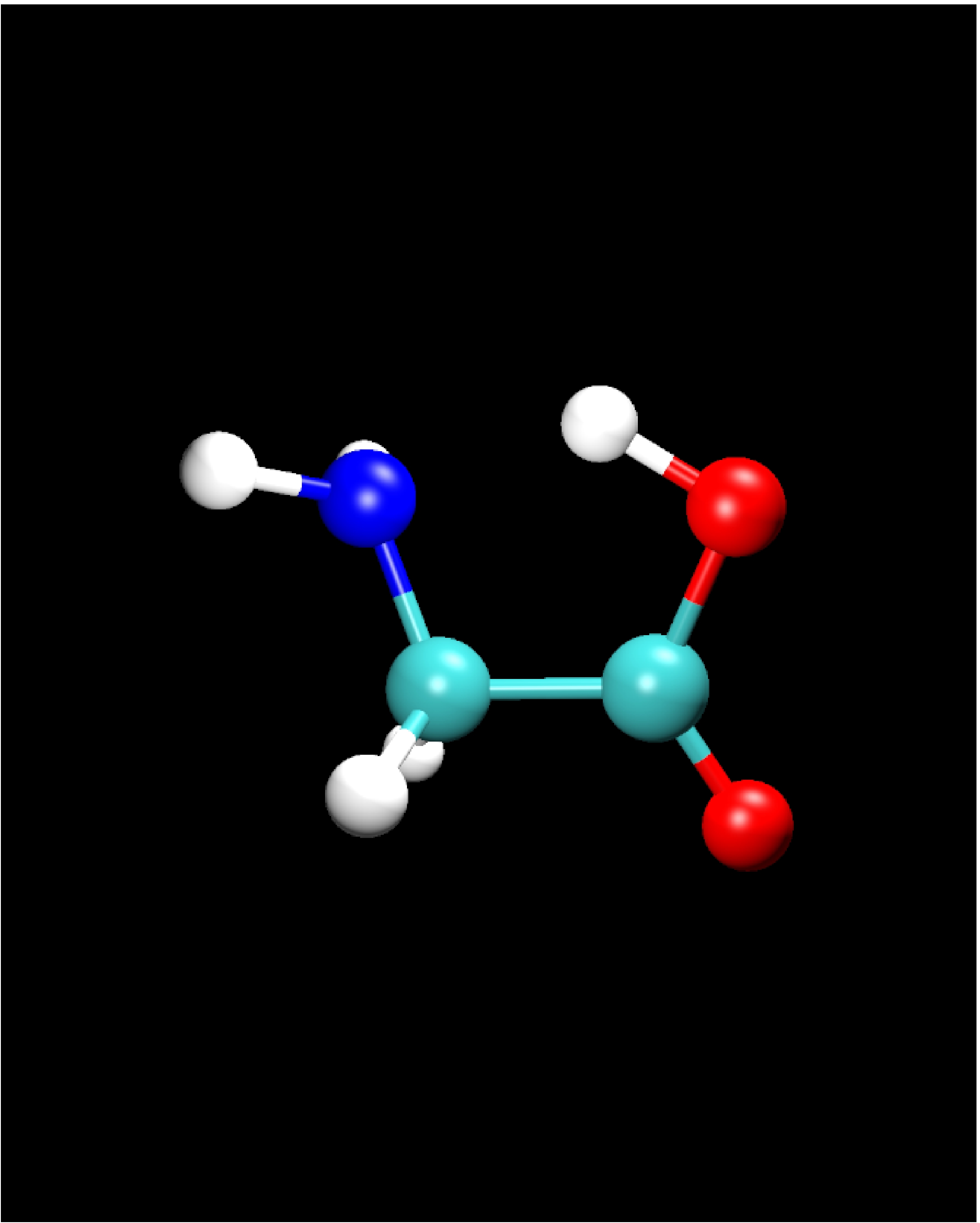
II.3) Glycine IIn

Calculational parameters xc-functional LDA [5] cut-off energy 80 Rydberg pseudopotential Troullier-Martins [3] nonlinear core corrections no supercell size 23 Bohr Results bond lengths [Angstroms] bond angles [degrees] bond LDA angle LDA N-H 1.021 H-N-H 108.5 N-C 1.452 H-N-C 113.7 C-H 1.099 N-C-C 110.3 C-C 1.518 H-C-H 106.2 C-O 1.330 C-C-O 112.0 C=O 1.206 C-C=O 123.1 O-H 1.029 C-O-H 101.3

III) Results for Alanine

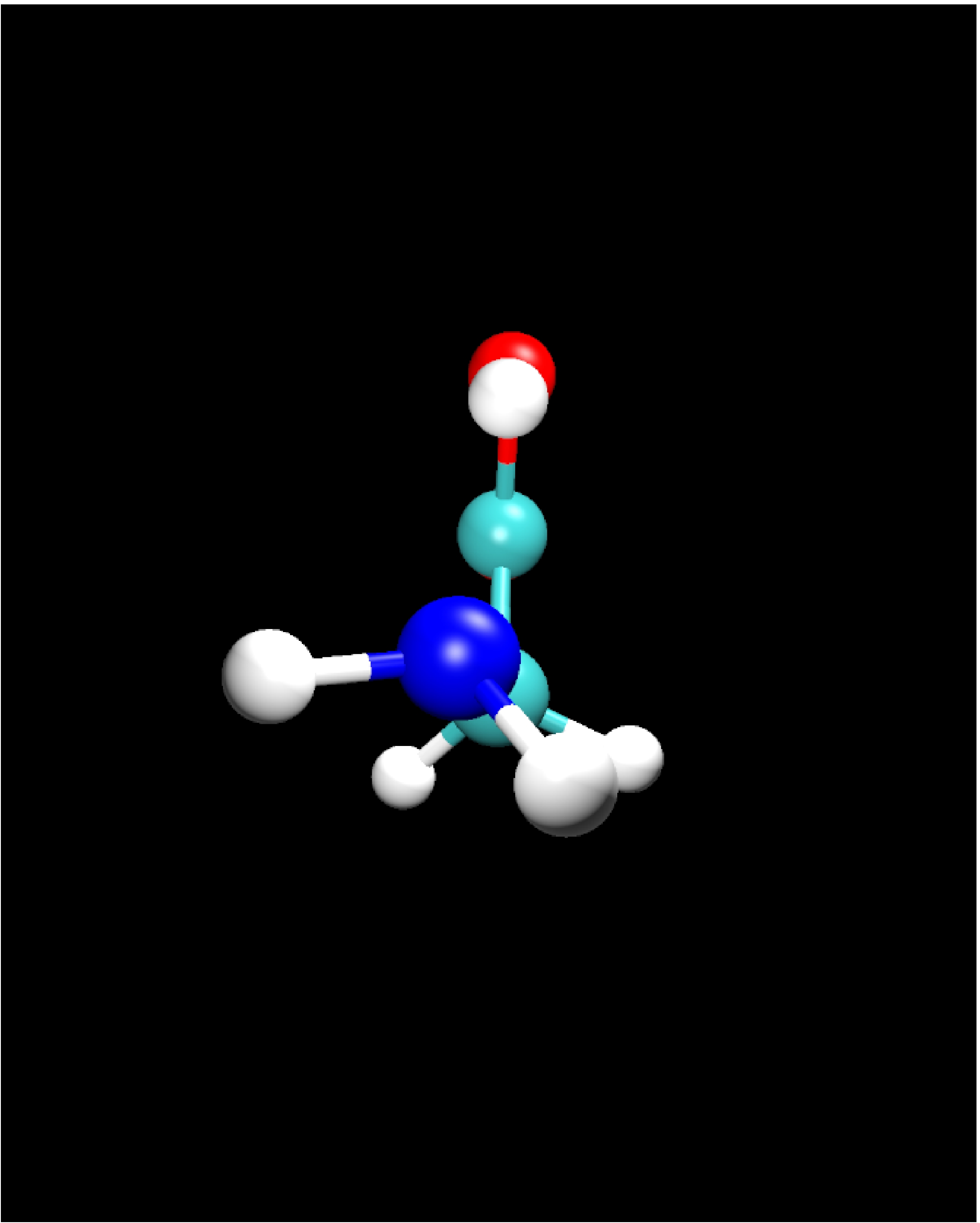
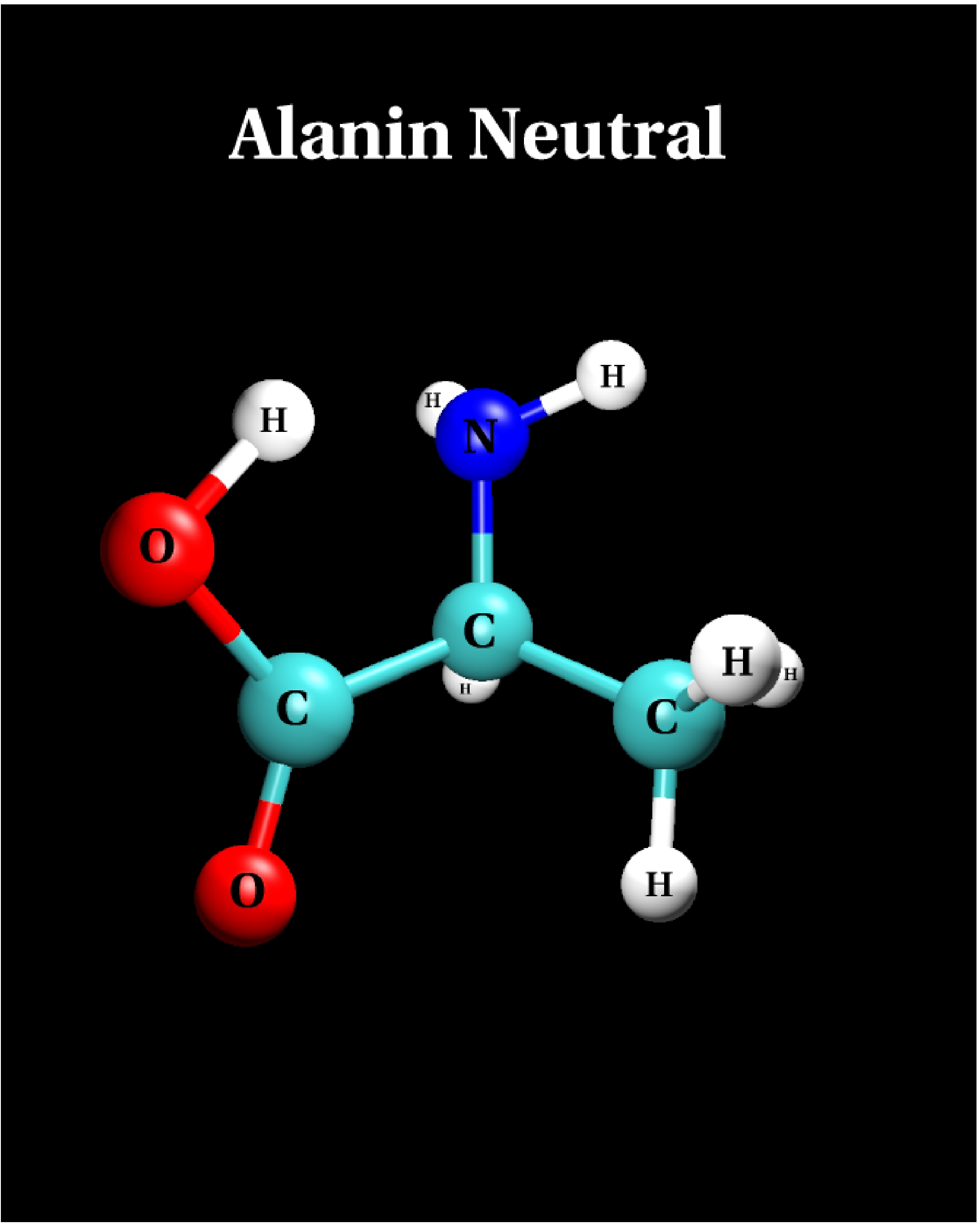
III.1) Neutral structure

Calculational parameters xc-functional LDA [5] cut-off energy 60 Rydberg pseudopotential Troullier-Martins [3] nonlinear core corrections no supercell size 23 Bohr Results bond lengths [Angstroms] bond angles [degrees] bond LDA angle LDA N-C 1.458 - - C-C 1.526 N-C-C 108.3 C-O 1.334 C-C-O 112.6 C=O 1.230 C-C=O 122.3 The LDA predicts the neutral structure to be the ground state configuration if alanine, in contrast to quantum chemical results [10]. The LDA energy difference to the zwitterionic state is 0.94 eV.

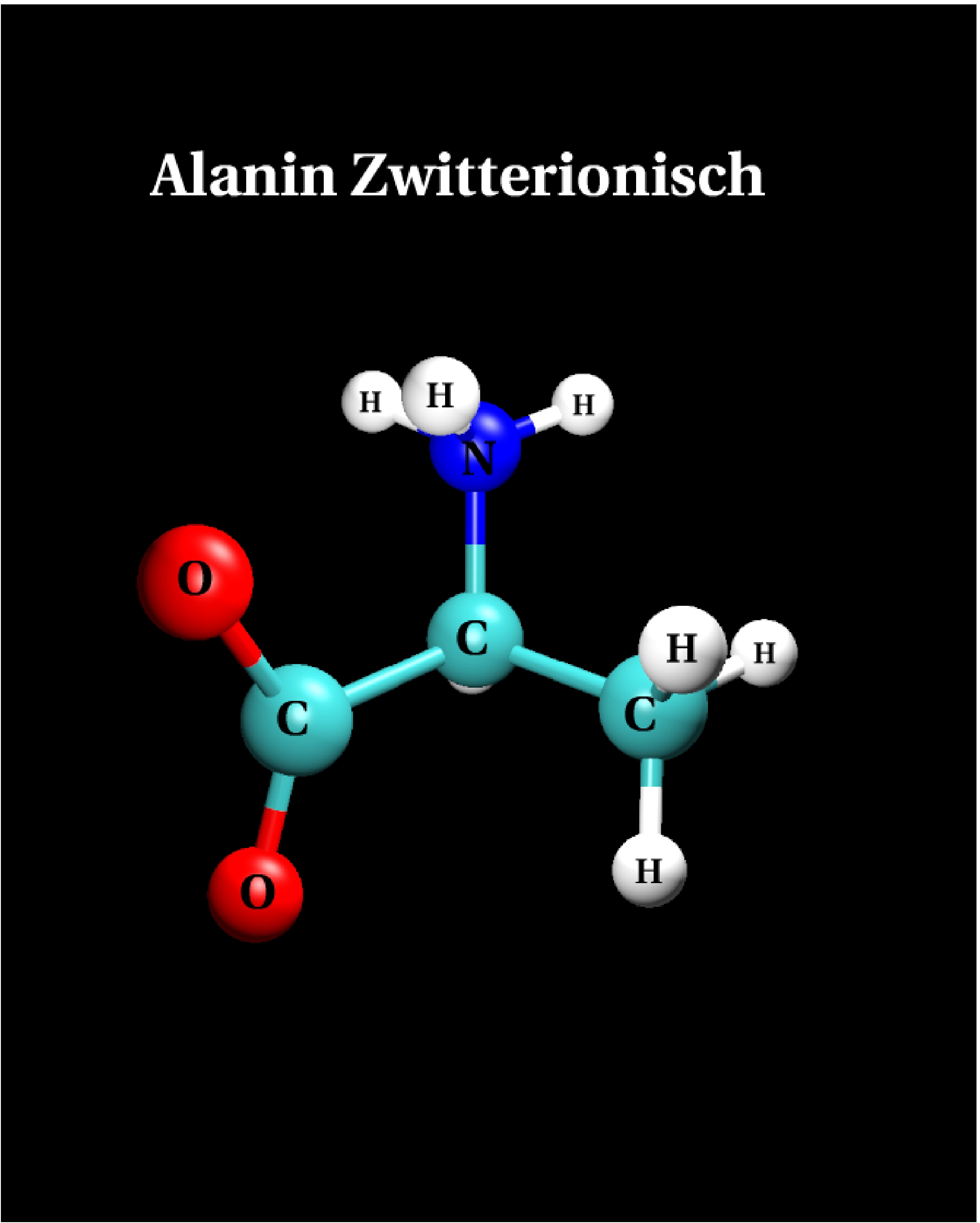
III.2) Zwitterion

Calculational parameters xc-functional LDA [5] cut-off energy 60 Rydberg pseudopotential Troullier-Martins [3] nonlinear core corrections no supercell size 23 Bohr Results bond lengths [Angstroms] bond angles [degrees] bond LDA angle LDA N-C 1.481 - - C-C 1.564 N-C-C 106.6 C-O 1.287 C-C-O 115.5 C=O 1.251 C-C=O 116.6

IV) Results for Serine

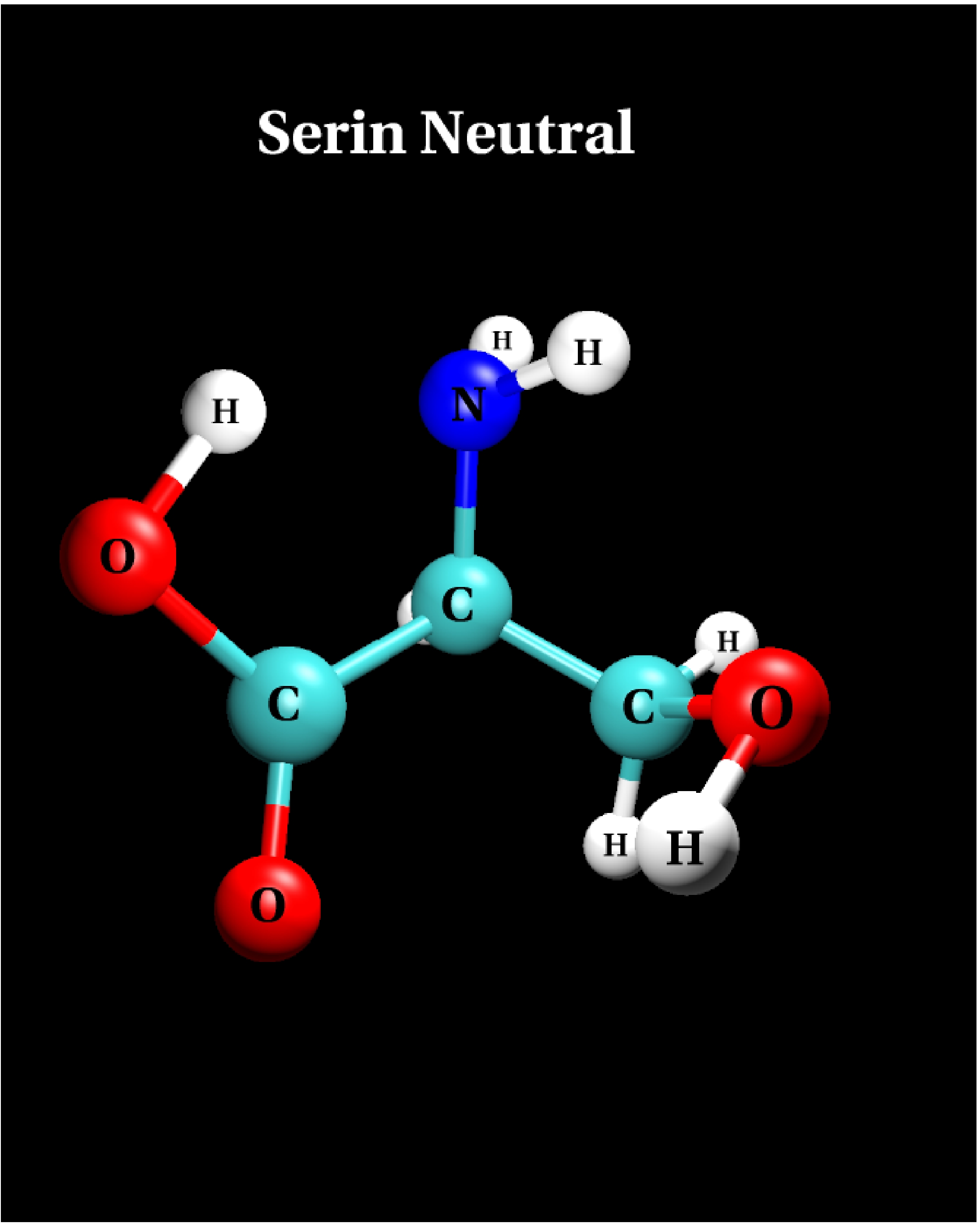
IV.1) Ground state

Calculational parameters xc-functional LDA [5] cut-off energy 60 Rydberg pseudopotential Troullier-Martins [3] nonlinear core corrections no supercell size 23 Bohr Results bond lengths [Angstroms] bond angles [degrees] bond LDA angle LDA N-H 1.028 H-N-H 108.6 N-C 1.452 H-N-C 113.2 C-H 1.107 N-C-C 107.0 C-C 1.528 H-C-H 109.0 C-O 1.333 C-C-O 112.4 C=O 1.232 C-C=O 122.3 O-H 1.054 C-O-H 99.4

References

1. G. Iseri, Diploma thesis, University of Frankfurt (2003).
2. M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias, and J. D. Joannopoulos, Rev. Mod. Phys. 64, 1045 (1992).
3. N. Troullier and J. L. Martins, Phys. Rev. B 43, 1993 (1991).
4. L. Kleinman and D. M. Bylander, Phys. Rev. Lett. 4, 1425 (1982).
5. S. H. Vosko, L. Wilk, and M. Nusair, Can. J. Phys. 58, 1200 (1980).
6. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh, and C. Fiolhais, Phys. Rev. B 46, 6671 (1992).
7. E. Engel, A. Höck, R. N. Schmid, R. M. Dreizler, and N. Chetty, Phys. Rev. B 64, 125111 (2001).
8. S. G. Louie, S. Froyen, and M. L. Cohen, Phys. Rev. B 26, 1738 (1982).
9. Iijima, Tanaka, Onuma, J. Mol. Struct. 246, 257 (1991).
10. F. R. Tortonda, J.-L. Pascual-Ahuir, E. Silla, and I. Tunon, J. Chem. Phys. 109, 592 (1998).

Last modified: April 2, 2004