2-Particle density: Correlated motion of electrons
The basic definitions of the 1- and 2-particle densities for given
N-particle state are
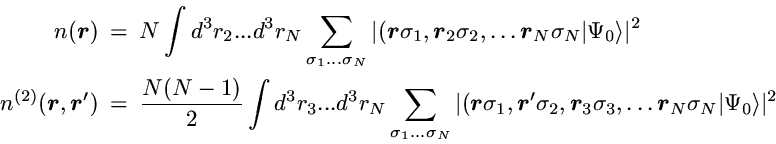
 The 2-particle density represents the probability to find one particle
with arbitrary spin at position r and simultaneously a second
particle with arbitrary spin at position r'.
The 2-particle density represents the probability to find one particle
with arbitrary spin at position r and simultaneously a second
particle with arbitrary spin at position r'.
In the case of noninteracting spin-1/2 particles the
N-particle state reduces to a Slater determinant
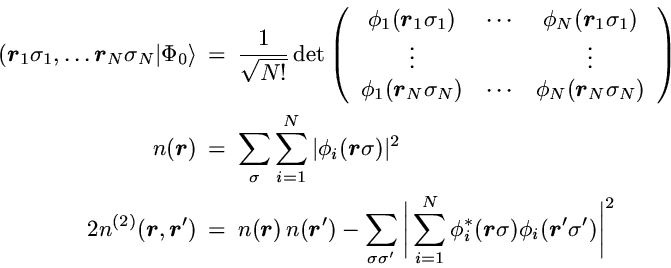
 The first term in the 2-particle density is the direct product of the
probability for finding one particle at point r with the
probability to find a particle at r'.
If the motion of the particles was completely uncorrelated this
product of single-particle probabilities would be the exact result.
However, in contrast to classical particles the spin-1/2 fermions
are correlated by the Pauli principle, even if a particle-particle
interaction is not present.
This so-called Pauli correlation is provided by the second
term.
The first term in the 2-particle density is the direct product of the
probability for finding one particle at point r with the
probability to find a particle at r'.
If the motion of the particles was completely uncorrelated this
product of single-particle probabilities would be the exact result.
However, in contrast to classical particles the spin-1/2 fermions
are correlated by the Pauli principle, even if a particle-particle
interaction is not present.
This so-called Pauli correlation is provided by the second
term.
For Helium the exact ground state wavefunction has the form
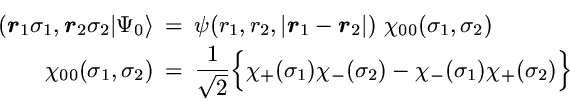
 Due to the spherical symmetry only 3 spatial coordinates are relevant.
One usually chooses the distances
r1 and
r2 between the electrons
and the nucleus (located at the origin) as well as the distance
between the two electrons.
The 1- and 2-particle densities are then simply given by
Due to the spherical symmetry only 3 spatial coordinates are relevant.
One usually chooses the distances
r1 and
r2 between the electrons
and the nucleus (located at the origin) as well as the distance
between the two electrons.
The 1- and 2-particle densities are then simply given by
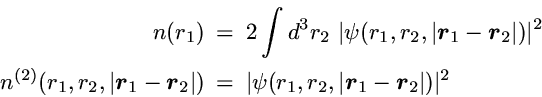
Within an effective single-particle description, as the Hartree-Fock
or the Kohn-Sham approach, the Helium ground state reduces to a product
of single-particle orbitals
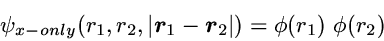
While the correlated motion of the two electrons essentially does not
show up in the 1-particle density - at least as long as a high quality
effective single-particle method is used - it is immediately visible in
the 2-particle density, as demonstrated subsequently.
In all plots the position of the nucleus defines the origin.
The first electron is kept fixed at different positions on the
x-axis (left-right axis), while the position of the
second electron is varied.
Shown is the probability to find the second electron anywhere in the
plane defined by the positions of the three particles.
The precise quantity plotted is the radial 2-particle density
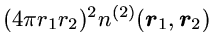
which is chosen so that integration over
r2
yields the standard radial density
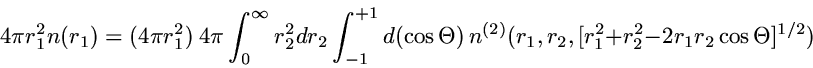
For the exact ground state a very accurate variational wavefunction [1]
is utilized (see Appendix).
The effective single-particle wavefunction has been obtained via the
Optimized Potential Method, using the exact
exchange functional of density functional theory.
Atomic units are used for all length scales.
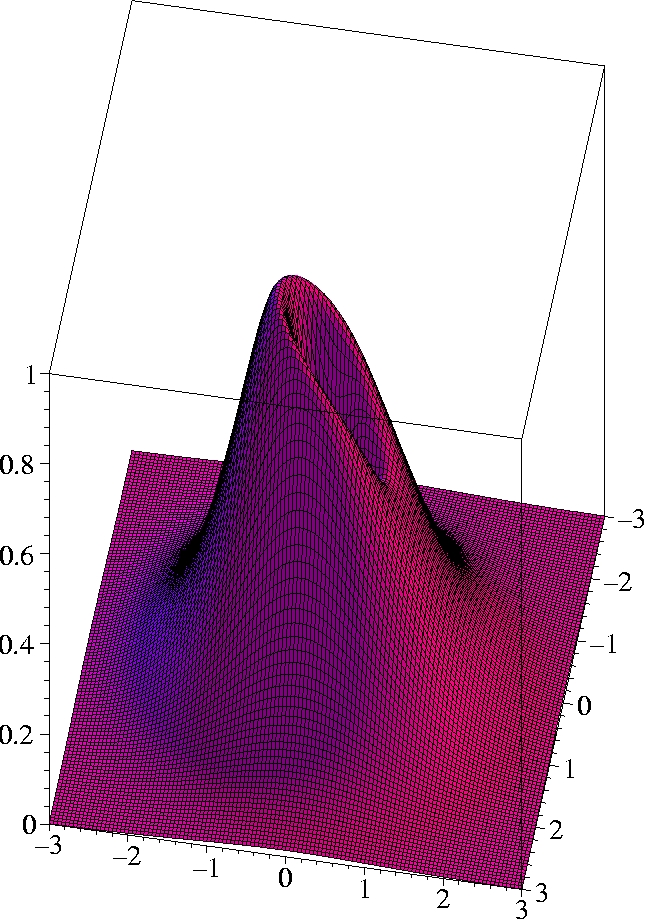
I) Exact 2-particle density of Helium:
r1=(0.559 Bohr, 0, 0) -
complete view
 x
x [Bohr]
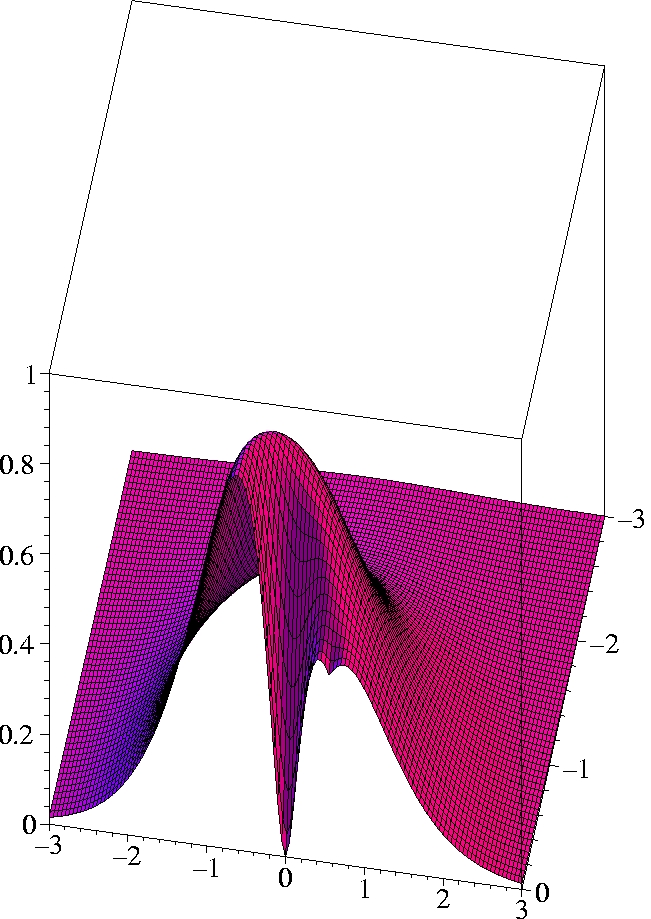
II) Exact 2-particle density of Helium:
r1=(0.559 Bohr, 0, 0) -
half plane only
 x
x [Bohr]
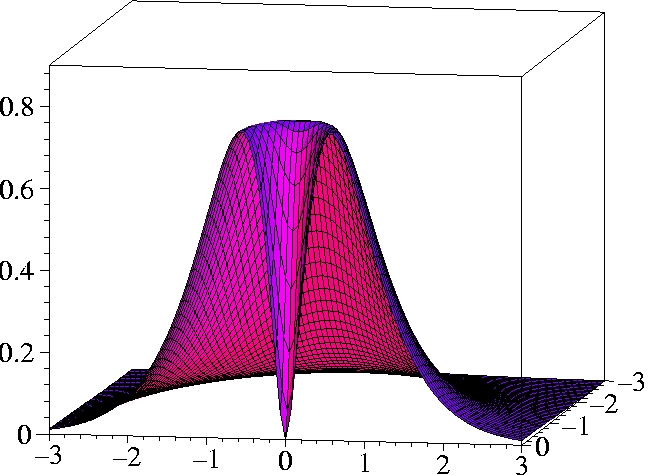
III) Kohn-Sham 2-particle density of Helium:
r1=(0.559 Bohr, 0, 0) -
half plane only
x [Bohr]
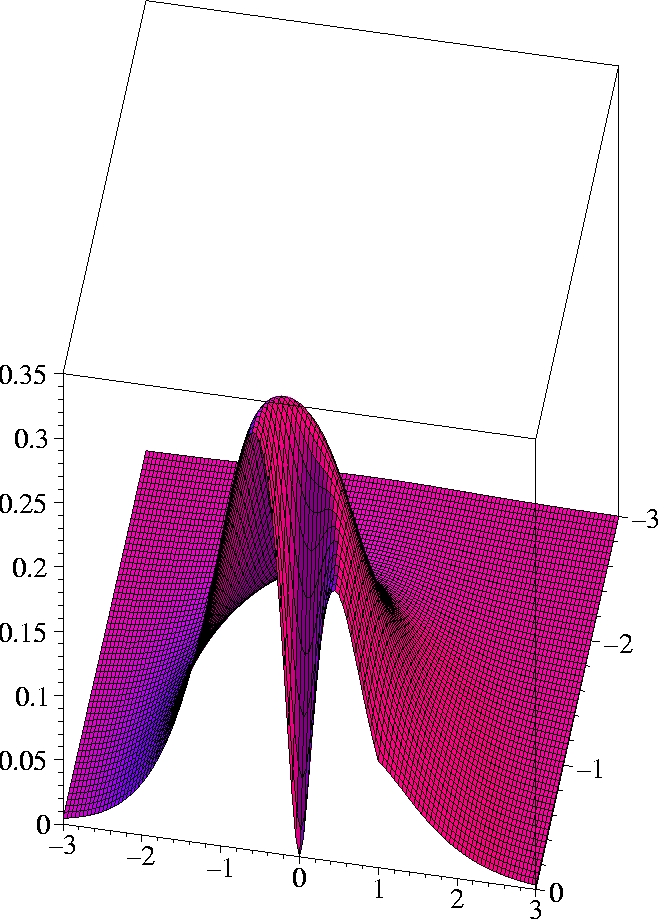
IV) Exact 2-particle density of Helium:
r1=(1.0 Bohr, 0, 0)
 x
x [Bohr]
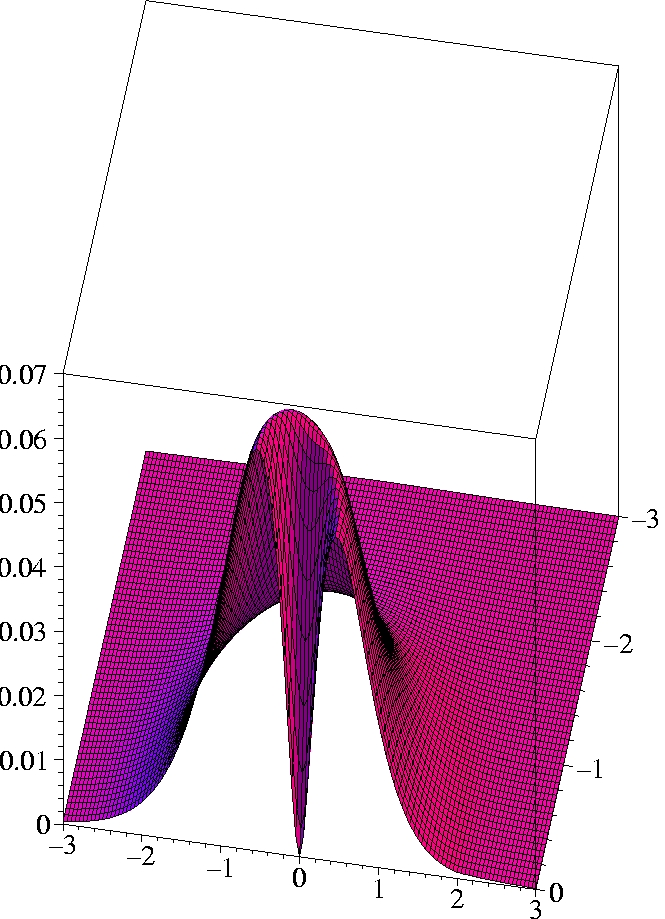
V) Exact 2-particle density of Helium:
r1=(2.0 Bohr, 0, 0)
 x
x [Bohr]
Observations:
-
The two electrons preferably move on opposite sides of the nucleus:
The likelihood to come close to each other is only half as large as
that of remaining on opposite sides
(Coulomb correlation).
-
The 2-particle density clearly shows the electron-electron cusp at
r1=
r2,
reflecting the short-range Coulomb repulsion.
-
While the KS ground state reproduces the exact ground state density
exactly, the KS determinant can not reproduce the exact 2-particle
density even qualitatively.
The motion of the two electrons (Kohn-Sham particles) is uncorrelated.
The correlated wavefunction used for this comparison is the most
elaborate variational wavefunction (38 parameters) given in the
original work of Kinoshita [1].
It has the form
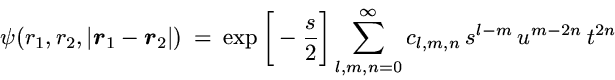
with
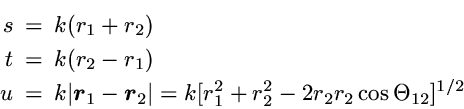
and
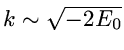 ,
,
 = variational parameters
= variational parameters
-
T. Kinoshita,
Phys. Rev. 105, 1490 (1957).
Home
Top
Last modified: Mar 31, 2004
Disclaimer
ee
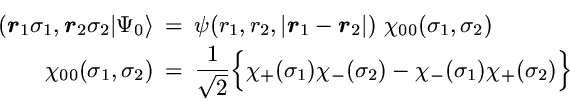
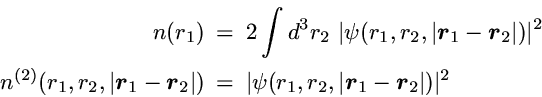
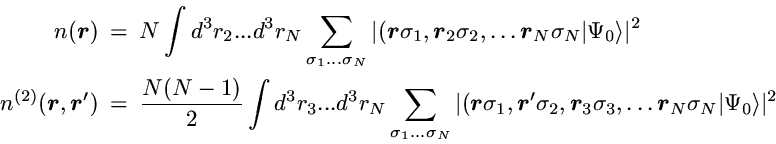
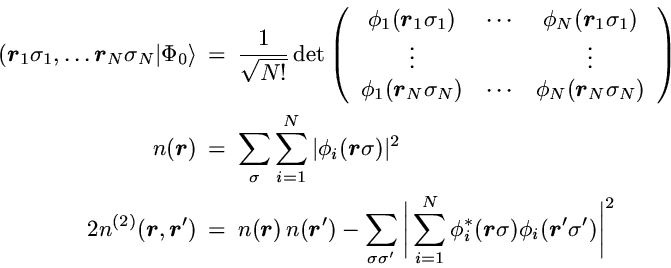
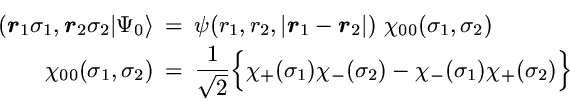
![]() Due to the spherical symmetry only 3 spatial coordinates are relevant.
One usually chooses the distances
r1 and
r2 between the electrons
and the nucleus (located at the origin) as well as the distance
between the two electrons.
The 1- and 2-particle densities are then simply given by
Due to the spherical symmetry only 3 spatial coordinates are relevant.
One usually chooses the distances
r1 and
r2 between the electrons
and the nucleus (located at the origin) as well as the distance
between the two electrons.
The 1- and 2-particle densities are then simply given by
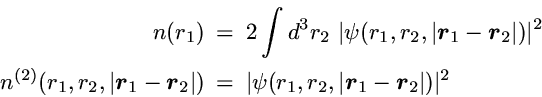
![]()
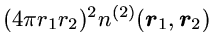
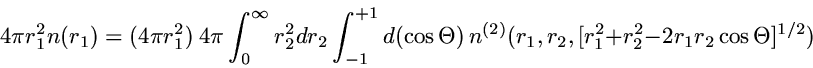





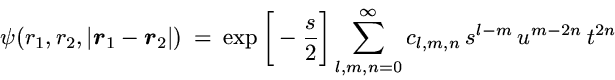
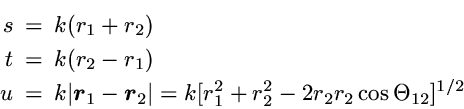
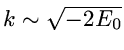 ,
,
![]() = variational parameters
= variational parameters