

Links: Von einem Scanner gelieferte Punkte. Mitte: Die triangulierte
Punktemenge. Rechts: Das segmentierte Dreiecksnetz.
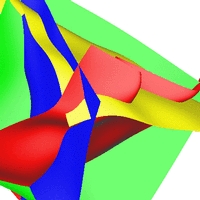
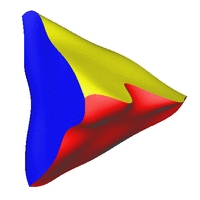
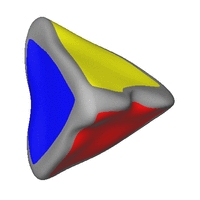
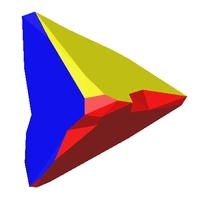
Links: Die approximierten Segmente. Mitte: Das fertige C0-stetige
CAD-Modell. Rechts: Das fertige C2-stetige CAD-Modell.
Rekonstruktion glatter Oberflächen mit getrimmten B-Spline-Flächen
Diplomarbeit im Fach Informatik
Marc Wagner
4. September 2002
In den folgenden Abschnitten wird das Thema meiner Diplomarbeit beschrieben und die in ihrem Rahmen erzielten Ergebnisse präsentiert. Die Funktionsweisen der von mir entwickelten Verfahren werden ausführlich in der dazugehörigen schriftlichen Ausarbeitung erläutert.
Reverse Engineering
Im Gegensatz zum normalen Engineering, bei dem aus einem vorhandenen Computermodell ein real existierender Gegenstand gefertigt wird, versucht man beim Reverse-Engineering aus einem bereits existierenden Gegenstand ein Computermodell zu erzeugen.
Reverse-Engineering ist ein Prozess, der in vielen Bereichen der Industrie, der Technik und der Medizin Anwendung findet. Einige Beispiele dafür werden im Folgenden genannt:



Links: Von einem Scanner gelieferte Punkte. Mitte: Die triangulierte
Punktemenge. Rechts: Das segmentierte Dreiecksnetz.



Links: Die approximierten Segmente. Mitte: Das fertige C0-stetige
CAD-Modell. Rechts: Das fertige C2-stetige CAD-Modell.
Zielsetzung dieser Arbeit
Die Zielsetzung dieser Arbeit bestand darin, Methoden zu entwickeln, die aus einem gegebenen Dreiecksnetz eine glatte C2-stetige Oberfläche erzeugen. Einige wenige C0-stetige Übergänge, die im Dreiecksnetz vorhandenen scharfen Kanten entsprechen, müssen auf Wunsch des Benutzers in die Gesamtfläche integriert werden können.
Um die erzeugte Oberfläche mit Standard-CAD-Software weiterverarbeiten zu können, muss diese in B-Spline-Form darstellbar sein (die Standardbeschreibung von Freiformflächen in kommerziellen CAD-Systemen sind TP-Bezier-Flächen oder TP-B-Spline-Flächen). Bei allen verwendeten Teilflächen muss es sich also um eventuell von Polynomkurven getrimmte bivariate Polynome handeln.
Diese Arbeit stellt die logische Fortsetzung der Dissertation meines Betreuers Kai Hormann dar und wurde auch als solche geplant. Dazu passend werden im Folgenden die beiden abschließenden Sätze seiner Arbeit zitiert:
"Especially in the context of smooth surface fitting, segmentation of the given data leads to the further question of how to join the single surface patches that approximate the individual subsets of data to give an overall reconstruction surface. While a non-differentiable joint along a crest line might be realized by trimming two neighbouring surface patches along the common intersection curve, blending with a higher order of continuity remains an open and unsolved problem".
Das Hauptaugenmerk richtet sich daher auf die Realisierung von C0-stetigen beziehungsweise C2 -stetigen Übergängen zwischen Primärflächen, die ein gegebenes Dreiecksnetz approximieren.
C0-stetige Übergänge zwischen Primärflächen
C0-stetige Übergänge zwischen zwei Primärflächen werden durch Berechnung geeigneter Trimming-Kurven realisiert.
Idealer Weise verlaufen die den Trimming-Kurven zugeordneten Raumkurven genau auf der Schnittkurve der entsprechenden Flächen. Da es sich sowohl bei den approximierenden Flächen als auch bei den zugeordneten Trimming-Kurven um Polynome handeln muss, scheidet eine exakte Lösung aus (die Schnittkurve zweier Polynomflächen ist im Allgemeinen keine Polynomkurve!). Folglich wurde ein numerisches Verfahren zur Approximation der Schnittkurven in jeweils beiden zugeordneten Parametergebieten entwickelt. Die damit erzielten Übergänge sind bis auf eine vom Anwender vorzugebende Toleranzgrenze C0-stetig.
In den folgenden Abbildungen sind einige C0-stetige CAD-Modelle zu sehen, die mit dem von mir entwickelten Verfahren erzeugt wurden.


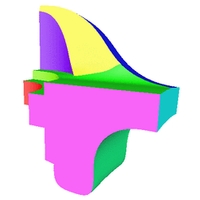
C0-stetige Rekonstruktionen verschiedener Oberflächen.
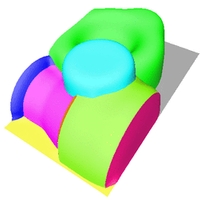
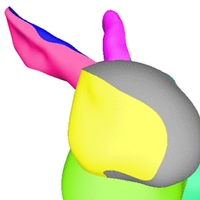
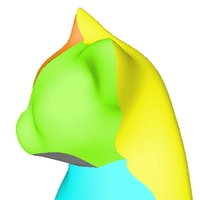
C0-stetige Rekonstruktionen verschiedener Oberflächen.
C2-stetige Übergänge zwischen Primärflächen
C2-stetige Übergänge zwischen approximierenden Primärflächen werden durch Berechnung geeigneter Blending-Flächen realisiert. Blending-Flächen lassen sich in zwei Klassen einteilen, Blending-Streifen und N-flächige Blends. Blending-Streifen bilden den Übergang zwischen zwei Primärflächen während N-flächige Blends N>=3 Primärflächen ineinander überblenden.
Die C2-stetige Gesamtfläche setzt sich folglich aus drei Arten von Flächen zusammen:
In den folgenden Abbildungen sind einige C2-stetige CAD-Modelle zu sehen, die mit dem von mir entwickelten Verfahren erzeugt wurden.
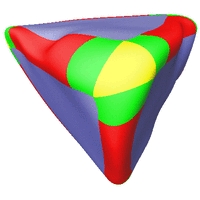
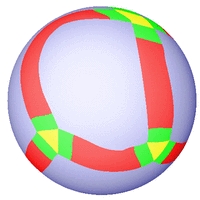
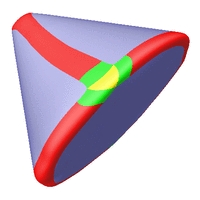
C2-stetige Rekonstruktionen verschiedener Oberflächen.

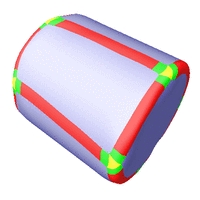

C2-stetige Rekonstruktionen verschiedener Oberflächen.
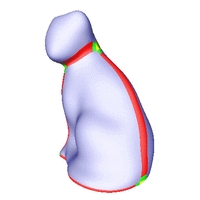
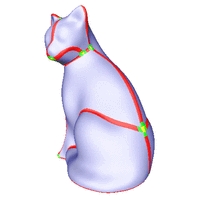
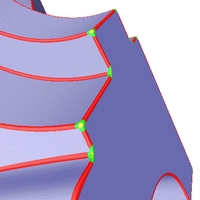
C2-stetige Rekonstruktionen verschiedener Oberflächen.
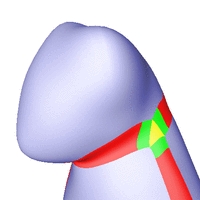
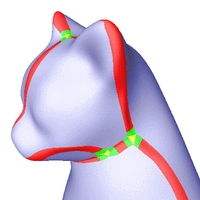
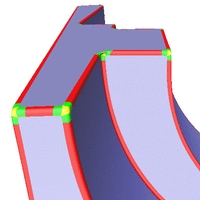
C2-stetige Rekonstruktionen verschiedener Oberflächen.