What does 'critical' mean?
Experimental observations
via stochastic sampling
versus intrinsic system properties.


Claudius Gros, Dimitrije Markovic

Institut für theoretische Physik
Goethe-Universität Frankfurt a.M.

Overview


generating powerlaws: established (?) routes


attractors in critical systems






infinite time-scale separation in sandpiles


× [C. Gros, Complex and Adaptive Dynamical Systems, Springer 2008/10/13/15]


$\ \color{darkRed}\Longrightarrow\ $ mapping to critical branching $(p=1/2)$ in infinite dimesion
$\ \color{darkRed}\Longrightarrow\ $ powerlaws





×

rich gets richer


Internet 2011: in-degree distribution
large-scale crawl, 32 Million most important sites, 2011
× [Gros, Kaczor, Markovic, EPJB 2012,
Neuropsychological constraints to human data production on a global scale]
- data availabe for further analysis -

generating powerlaws via
preferential attachment

[Barabasi, Albert, ...]
$$ p_k\ \sim\ \frac{1}{k^\gamma},\qquad \gamma = 1+\frac{1}{1-r/2} $$ $\ \color{darkRed}\Longrightarrow\ $ mostly internal growth




continuously active networks


[Markovic, Gros, Powerlaws and Self-Organized Criticality in Theory and Nature, Physics Reports 2014]

[Gazzaley & Rosedale]

×

absorbing phase transition:

external drivings couple to order parameter

×

external fields coupling to order parameter

destroy the phase transition







two viewpoints

humans maximizing Shannon information

maximal entropy distributions

with constraint $\displaystyle\quad \langle x\rangle=\mathrm{const.} \qquad\quad\color{darkBlue}{p(x)\ \propto\ \mathrm{e}^{-\lambda x} }$

Weber-Fechner law

$$\scriptstyle \begin{array}{llcll} \color{darkGreen}{\mathrm{music:}} & \mathrm{tone\ pitch} &\propto& \log(\mathrm{frequency}) & \color{darkGreen}{\mathrm{(octave)}} \\ \color{darkGreen}{\mathrm{photometry:}} & \mathrm{brightness} &\propto& \log(\mathrm{intensity}) & \color{darkGreen}{\mathrm{(lumen)}} \\ \color{darkGreen}{\mathrm{acoustics:}} & \mathrm{sound\ level} &\propto& \log(\mathrm{intensity}) & \color{darkGreen}{\mathrm{(decibel)}} \\ \end{array} $$
$$ \color{darkBlue}{x\ \to\ \log(x)} \qquad \color{darkRed}{\Rightarrow} \qquad \color{darkBlue}{p(x)\ \to\ \mathrm{e}^{-\lambda \log(x)} \ \propto\ \frac{1}{x^\gamma} } $$ $\ \color{darkRed}\Longrightarrow\ $ scale invariant distributions




publicly available data files in the internet


[Gros, Kaczor, Markovic, EPJB 2012]






distribution of 2-dimensional data files


[Gros, Kaczor, Markovic, EPJB 2012]








$\ \color{darkGreen}\Longrightarrow\ $ log-normal
distributions


maximal entropy distributions for 2D data

$$\color{darkBlue}{ p(x,y)\ \ \propto\ \ \mathrm{e}^{-\,\lambda_1\, xy\, -\,\lambda_2\, x^2\,-\,\lambda_3\, y^2} \ \ =\ \ \mathrm{e}^{-\,\lambda[\alpha\color{darkGreen}{(x+y)}\,+\, \beta\color{darkGreen}{(x-y)}]^2} }$$ logarithmic discounting $$\quad \quad \color{darkGreen}{ x+y \ \ \to\ \ \log(xy) \qquad\qquad x-y \ \ \to\ \ \log(x/y) }$$
× [Gros, Kaczor, Markovic, EPJB 2012]
$$\color{darkBlue}{ p(x,y)\ \ \propto\ \ \mathrm{e}^{-\,\lambda''\, \log^2(xy)\, -\,\lambda'\, \log(xy)} }$$




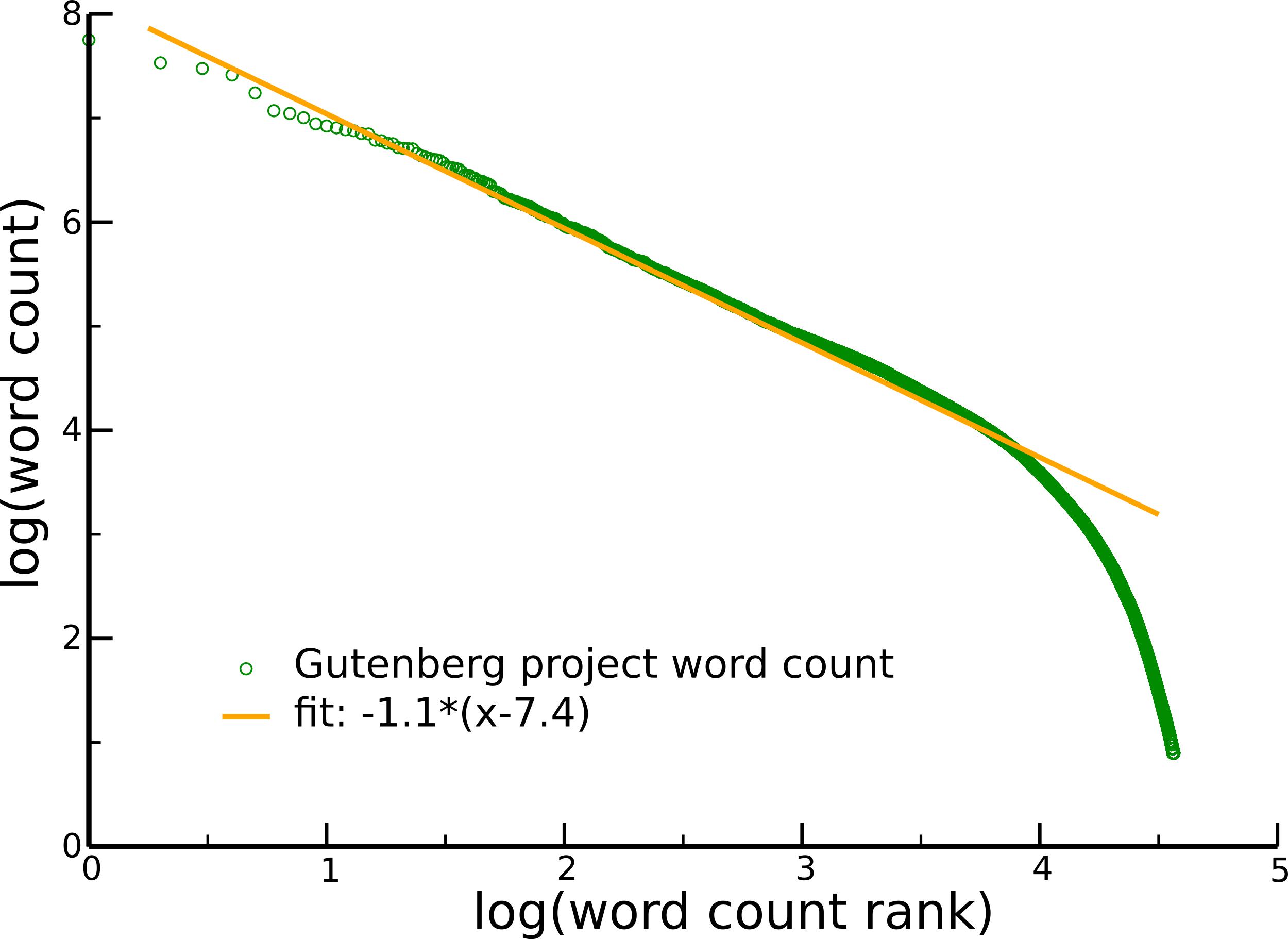
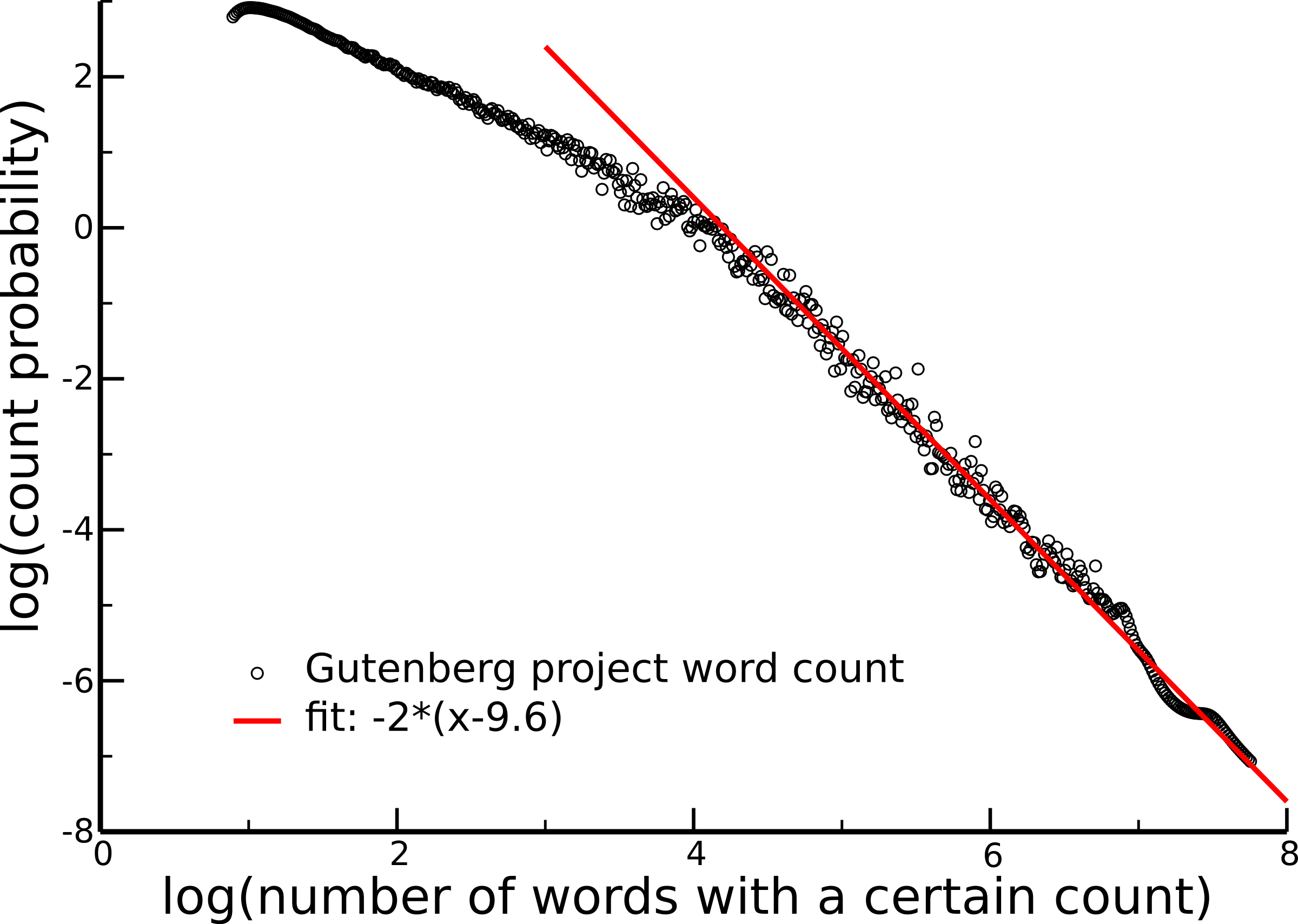
rank count vs. count probability

[Zipf '49, Cancho & Sole `03]$\qquad\quad$

40.000 most frequent (english) words


   
$$\color{orange}{\left(\frac{1}{R}\right)^\gamma}$$ $$\color{red}{\left(\frac{1}{C}\right)^{1+1/\gamma}}$$





wrap up - generating powerlaws


some stablished routes


... next: observing powerlaws






NK / Kauffman networks

   




[Luque & Sole, ‘00]

$$ \begin{array}{rcl} N & : & \mathrm{number\ of\ sites} \\ K & : & \mathrm{number\ of\ controlling\ elements} \\ \Sigma &= & (\sigma_1,\dots,\sigma_N), \qquad\quad \sigma_i=\pm1 \end{array} $$


×
N=7 K=3


state perturbed state

converge, if within the same basin of attraction


number of (cyclic) attrators

$$ \begin{array}{rcl} \color{darkOrange}{\mathrm{Kauffman\ '69:}} &\sim& \sqrt{N} \\ &\Rightarrow& \color{darkGreen}{\mathrm{cell\ differentiation}}\\[1.0ex] \color{darkOrange}{\mathrm{Samuelsson\ \&\ Troein\ '03:}} &>& O(N^p) \ \ \mbox{(any p)} \end{array} $$

are these (additional) small attrators relevant?






vertex routing models


transmission vs. routing

transmission routing
vertex $\ \color{darkOrange}{\Rightarrow}\ $ vertex link (incomming) $\ \color{darkOrange}{\Rightarrow}\ $ link (outgoing)
dynamical variables: vertices dynamical variables: links
$\qquad\qquad$
[Markovic & Gros, New Journal of Physics `09]




routing dynamics



$\quad$ conserved? $\quad$
$\quad$ $\quad$
yes $\quad$ $\quad$ no
$\quad$ $\quad$
$\quad$ memory? $\quad$





cyclic attractors



random walks through configuration space

number of cycles of length $L$


no memory with memory
$$ \frac{N!}{L(N-1)^{L}(N-L)!} $$ $\qquad$ $$ \frac{N((N-1)^{2})!}{L(N-1)^{2L-1}((N-1)^{2}+1-L)!} $$

$$ \begin{array}{rcl} \color{red}{\langle n\rangle} &:& \mathrm{number\ of\ cycles}\\ \color{black}{\langle T\rangle} &:& \mathrm{cumulative\ cycle\ length} \\[1ex] \color{black}{\langle T\rangle}/\color{red}{\langle n\rangle} &:& \mathrm{mean\ cycle\ length} \\ &\sim& N/\log(N) \end{array} $$
× $$ \begin{array}{rclcl} \color{red}{\langle n\rangle} &:& \mathrm{number\ of\ cycles} &\sim& \color{darkOrange}{\log(\Omega)=2\log(N)} \\ \color{black}{\langle T\rangle} &:& \mathrm{cumulative\ cycle\ length} &\sim& \color{darkOrange}{\sqrt{\Omega}=N} \end{array} $$ [Markovic, Schuelein & Gros, Chaos `13]





stochastig sampling of phase space

experimental observation / biologically active networks

$$ \begin{array}{rcl} \mathrm{start\ randomly} &\color{darkRed}{\Rightarrow} & \mathrm{find\ next\ attractor}\\ &\color{darkRed}{\Rightarrow}& \mathrm{evaluate\ attractor\ properties} \end{array} $$

intrinsic
property		 stochastic
sampling
with memory number of cycles
mean cycle length 		$\log(N)$
$N/\log(N)$		 —
$N$
no memory number of cycles
mean cycle length 		$\log(N)$
$\sqrt{N}/\log(N)$		 —
$\sqrt{N}$
[Markovic, Schuelein & Gros, Chaos `13]





cycle length distribution








large and small basins of attractions


a Gedanken-distribution






criticality in statistical mechanics


second order phase transitions


what are observables?

$\quad \left\langle \sum_{states} \hat A(states)\,\mathrm{e}^{-\beta H(states)} \right\rangle $

thermodynamic averaging $\ \color{darkRed}{\hat=} \ $ stochastic sampling

$\hspace{5ex}\color{darkRed}\Longrightarrow\ $ `intrinsic properties' do not matter




classical thermalization and sampling

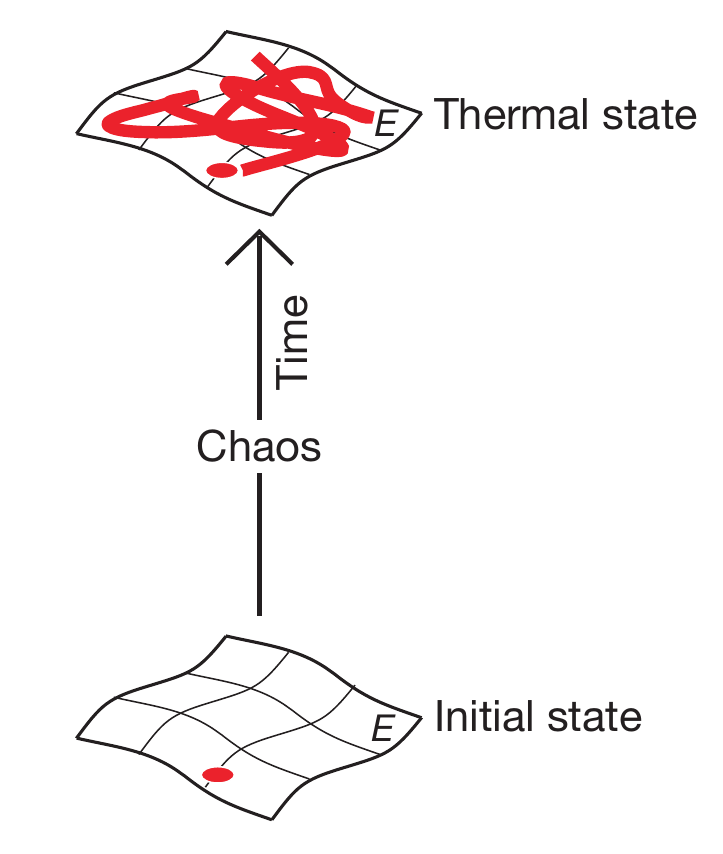[Rigol, Dunjko & Olshanii, Nature `08]

thermal states are 'typical' states


only regions in phase space contribute to the thermal state, which have a finite probability to be visited (closely) by chaotic trajectories

$\color{darkRed}{\Downarrow}$

regions in phase space which are not sampled by the internal dynamics do not contribute to the thermal state


caveat for dynamical systems: $\ \ $ thermalization at zero temperature?
$ \ \ $ energy not defined?

a given dynamical system may have interesting internal properties,
but in the end what matters is only what can be observed





textbook: complex systems